Учет коэффициента объединения по входу и коэффициента разветвления по выходу элементов при синтезе схем автоматов без памяти

Если допустимое количество входов выбранного элемента меньше, чем требуется, то приходится вводить дополнительные однотипные элементы и объединять их на основе сочетательного закона для дизъюнкции и конъюнкции, или применять те или иные скобочные формы. Это приводит к увеличению количества элементов и ярусов реализации схемы, т.е. к возрастанию задержки сигнала и снижению быстродействия рис. 2.5 а,б,в. В некоторых элементах при этом могут использоваться не все входы. Лишние входы должны быть присоединены к тем или иным точкам схемы (к клемме”земля” или к клемме “источник” - это оговаривается в руководстве по применению интегральных микросхем).

Например. Лишние входы могут быть присоединены к шине питания или к другим входам (рис.2.5 б,в).

При этом функционирование будет одним и тем же.

Впервом случае возрастает надежность (рис.2.5 а), но увеличивается нагрузка на предшествующий элемент. Это не всегда допустимо и к тому же приводит к увеличению задержки сигналов.

а) б) в)

Рисунок 2.5 - Схема объединения входов

Для элемента “И” подход должен быть несколько иным.

Лишние входы элемента здесь могут быть либо объединены с другими входами (рис.2.6 а), либо присоединены к “генератору единиц”, что для импульсного режима работы соответствует подаче тактирующих импульсов, а при потенциальных сигналах - присоединению к точке схемы с потенциалом, соответствующим сигналу 1 (рис. 2.6), или могут оставаться не подключенными ни к какой точке схемы.

а) б) в)

Рисунок 2.6 - Схемы объединения лишних входов

Учет при синтезе схем коэффициента разветвления элементов по выходу

Коэффициент разветвления n указывает максимально возможное число входов элементов, которые могут быть подключены к выходу данного элемента.

Любое увеличение количества подключаемых входов приводит к возрастанию задержки сигналов, а подключение их в количестве, превышающем коэффициент разветвления, приводит к недопустимому снижению помехоустойчивости и надежности функционирования. Существует два способа устранения перегрузок в схеме дублирования перегруженных элементов и введение развязывающих усилителей после перегруженных элементов. Пусть к выходу элемента “ИЛИ” подключаются пять входов логических элементов (рис. 2.7).

Рисунок 2.7 - Схема перегруженного элемента

Допустим, что элементы имеют коэффициент разветвления n = 3.

Тогда элемент ИЛИ перегружен по выходу, поскольку к нему подключаются пять входов последующих элементов.

На рис.2.8а,б использованы способы устранения перегрузки путем дублирования и развязывающих усилителей.

а) б)

Рисунок 2.8 - Схемы устранения перегрузок элементов

Введение дублированных элементов (рис. 2.8а) не вносит дополнительных задержек сигналов, но повышает нагрузку на предшествующие элементы. Разгрузка по второму способу (рис. 2.8б) всегда вносит дополнительную задержку на усилителях, включаемых последовательно с нагружаемыми элементами, но может оказаться более экономичной по сравнению с дублированием элементов, поскольку не увеличивает нагрузку на предшествующие элементы. Возможно применение комбинированного метода, при котором в некоторых случаях можно получить оптимальный вариант, обеспечивающий допустимые аппаратурные затраты и заданное быстродействие.

2.2 Комбинационные сумматоры

Одним из узлов арифметического устройства(АУ), в значительной степени определяющим скорость его работы, является сумматор.

Сумматор - это узел АУ, реализующий алгебраическое суммирование двух чисел, представленных сигналами на его входах. Обычно сумматор строят из так называемых одноразрядных сумматоров. Одноразрядный сумматор - это схема, имеющая два выхода и три входа, на которые могут быть поданы сигналы, представляющие цифры первого и второго слагаемых и цифру переноса из соседнего младшего разряда. Один выходной сигнал представляет цифру суммы, а другой - цифру переноса в соседний старший разряд.

Условное обозначение приведено на рис. 2.9.

Рисунок 2.9 - Условное обозначение сумматора

Функционирование одноразрядного сумматора на три входа (ОС-3) описывается таблицей 2.2. Здесь X, Y, Z - двоичные одноразрядные слагаемые, S - сумма в данном разряде, Р - перенос из данного разряда в следующий старший разряд.

СДНФ заданных функций имеет вид

S (X, Y, Z) =Z + Y + X + XYZ; (2.1)

Р (X, Y, Z) =YZ + XZ +XY + XYZ. (2.2)

Таблица 2.2

X	Y	Z	S	P
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Представим функции 2.1 и 2.2 в виде карт Карно

Непосредственная минимизация функций S и P приводит к следующим минимальным ДНФ

S (X, Y, Z) = Z + Y + X+ XYZ (2.3)

P (X, Y, Z) = XY + XZ + YZ (2.4)

Схема сумматора, реализующего соотношения 2.3 и 2.4, показана на рис.2.10.

Рисунок 2.10 - Схема сумматора

Выходные сигналы, формируемые сумматором, определяются комбинацией цифр слагаемых, одновременно поданных на его входы. Данный сумматор не обладает памятью, так как после снятия входных сигналов суммы и переноса, сигналы на его выходе также снимаются. Такие сумматоры называются комбинационными. Быстродействие одноразрядного комбинационного сумматора характеризуется временем установления выходных сигналов суммы и переноса после подачи сигналов на входы сумматора.

Помимо ОС-3 большое применение находят одноразрядные сумматоры на два входа (ОС-2), которые называются полусумматорами, или сумматорами по модулю 2. На основе последних очень просто и весьма экономно можно построить ОС-3. Схема такого сумматора приведена на рис. 2.11.

Рисунок 2.11 - Схема ОС-3 на основе двух ОС-2

Существуют два основных метода выполнения суммирования: последовательный и параллельный. При последовательном методе в сумматоре производится поразрядная обработка исходных чисел. Разряды чисел поступают последовательно один за другим, начиная с младших разрядов. При параллельном методе – суммирование всех разрядов чисел производится одновременно. Одноразрядный сумматор является основой последовательного сумматора и каждого разряда параллельного сумматора. Число одноразрядных суммирующих схем в параллельном сумматоре равно числу разрядов слагаемых.

Достоинством сумматоров последовательного действия являются малые аппаратурные затраты, поскольку для организации суммирования многоразрядных чисел здесь используется один ОС-3. Однако время выполнения операции сложения в сумматоре последовательного действия существенно больше, чем в сумматоре параллельного действия.

В многоразрядном сумматоре параллельного действия аппаратурные затраты значительно больше, чем в сумматоре последовательного действия, поскольку количество ОС-3, входящих в его состав, равно количеству разрядов операндов. Однако время выполнения операций здесь может быть сведено к минимуму.

Схема комбинационного многоразрядного сумматора последовательного действия приведена на рис. 1.26а. Его работа поясняется временными диаграммами, изображенными на рис. 1.26б, на примере сложения кодов двух чисел

[X]q = 1.1001; и [Y]q = 0.1101

a)

б)

Рисунок 2.12 - Схема последовательного многоразрядного сумматора

Слагаемые подаются на входы сумматора поразрядно, начиная с младших разрядов. Импульсы переноса P с выхода одноразрядного сумматора через элемент задержки на один такт поступает одновременно со старшим разрядом операндов на его третий вход. При этом на выходе S формируются сигналы разрядов суммы. Поскольку суммируются дополнительные коды слагаемых, то перенос из знакового разряда должен отбрасываться. Это обеспечивается с помощью элемента “И” в цепи переноса.

Время, необходимое для сложения двух n-разрядных чисел, можно определить по формуле

Тсч = (n-1)Δ (2.5)

здесь n - число разрядов в коде слагаемого;

Δ - длительность такта.

Сумматор параллельного действия может быть составлен из (n+1) одноразрядных сумматоров путем соединения их выходов, на которых формируются сигналы переноса, со входами соседних более старших разрядов. На рис. 2.13 показана схема нескольких разрядов такого параллельного сумматора. В нем цепь переноса из разряда в разряд получается последовательной. Сигнал переноса в каждом следующем разряде образуется только после сформирования сигнала в предыдущем разряде.

Рисунок 2.13 - Схема параллельного сумматора

Эта схема называется сумматором с последовательным переносом. Максимальное время суммирования равно

Тсч.маx. = t_ОС-3 + ntn, (2.4)

где: t_ОС-3 - время образования суммы в одноразрядном сумматоре на три входа;

tn - время распространения переноса в одном разряде.

Для уменьшения времени распространения сигнала переноса используются различные варианты схем сумматоров, наиболее распространенными из которых являются схемы со сквозным переносом, схемы с параллельным переносом и схемы с групповым переносом.

В сумматорах параллельного действия все разряды слагаемых поступают на вход сумматора одновременно. При этом операция сложения выполняется за 1 такт работы сумматора.

2.3. Особенности синтеза комбинационных схем на программируемых логических матрицах (ПЛМ)

Успехи в области интегральной технологии привели к созданию БИС с тысячами элементов на одном кристалле, позволившие повысить их надежность и быстродействие, снизить потребляемую мощность и габариты. Однако при этом возникла проблема: Как на схемах с таким количеством элементов изготовить устройства, реализующие различные функции, решающие разные задачи?

Казалось бы, заказные БИС. Но это дорого.

Выходом из создавшегося положения явились ПЛМ. Условное графическое изображение приведено на рис. 2.14.

Для создания устройства элементы соединяются между собой (осуществляется программирование схемы) на заключительном этапе изготовления по специальным шаблонам, с помощью которых образуются или разрушаются связи. Так как микросхемы этих устройств построены по матричному принципу, их называют ПЛМ.

Матрица - это сетка взаимно перпендикулярных проводников, в местах пересечения которых находятся диоды или транзисторы, включенные через предохранители. При программировании перемычки могут быть расплавлены.

Рисунок 2.14 - Условно-графическое изображение ПЛМ

Программируемая логическая матрица представляет собой матрицу вентилей, которую можно запрограммировать в виде различных комбинаций вентилей, реализующих логические функции дизъюнкции и конъюнкции. На их основе могут составляться сложные комбинационные логические схемы. Матрицы ПЛМ отличаются от постоянных запоминающих устройств только структурой и выпускаются в виде устройств, программируемых с помощью шаблона заводом изготовителем (К155 РЕ21 - 256х4 бит ПЗУ, К556 Р54 - 256х4 бит ППЗУ и устройств, программируемых пользователем). На рис. 2.15 показана схема матрицы, программируемой пользователем. Матрица содержит диоды, каждый из которых катодом подключен к строкам, а анодом - к столбцам; последовательно с каждым диодом включена плавкая вставка. На базе этой матрицы может быть сформирована конъюнктивная матрица, реализующая функции “ИЛИ”. Синтез логических схем на базе ПЛМ состоит в избирательном разрушении (пережигании) элементов структуры ПЛМ под действием приложенного электрического напряжения.

Рисунок 2.15 - Схема ПЛМ, программируемая пользователем

На рис. 2.16 представлена схема конъюнктивной матрицы, на горизонтальные шины которой подаются значения входных переменных X₁ - X₅, а с вертикальных шин снимаются значения конъюнкций Z₁ - Z₅.

Z₁ (X₁, X₂, X₃, X₄, X₅) = X₁ X₂ X₅.

Z₂ (X₁, X₂, X₃, X₄, X₅) = X₁ X₂ X₃ X₄.

Z₃ (X₁, X₂, X₃, X₄, X₅) = X₁ X₃ X₅.

Z₄ (X₁, X₂, X₃, X₄, X₅) = X₁ X₂ X₄ X₅.

Z₅ (X₁, X₂, X₃, X₄, X₅) = X₂ X₄ X₅.

В матрице имеются резисторы R, подключенные к вертикальным шинам. При наличии на катоде хотя бы одного диода нулевого потенциала (лог.”0") этот диод открывается и на соответствующей выходной вертикальной шине устанавливается также сигнал лог.”0".

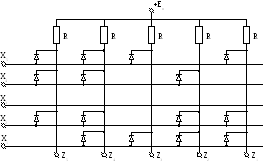
Рисунок 2.16 - Конъюнктивная ПЛМ на диодах

На рисунке 2.17 представлена схема дизъюнктивной матрицы, входные переменные в которой подаются на вертикальные шины, с горизонтальных шин снимаются значения дизъюнкций Z₁ - Z₅

Z₁ (X₁, Х₂, Х₃, Х₄, Х₅) = X₁ + Х₂ + Х₃ + Х₄;

Z₂ (X₁, Х₂, Х_З, Х₄, X₅) = X₁ + Х₂ + Х₄ + Х₅;

Z₃ (X₁, Х₂, Х₃, Х₄, Х₅) = Х₂ + Х₃;

Z₄ (X₁, Х₂, Х_З, Х₄, Х₅) = Х₂ + Х₄ + Х₅;

Z₅ (X₁, Х₂, Х_З, Х₄, Х₅) = X₁ + Х_З + Х₄ + Х₅.

Реализация более сложных функции возможна при объединении двух матриц: конъюнктивной или дизъюнктивной. Пример такой ПЛМ приведен на рисунке 2.18, где в вычислении функции участвуют две матрицы:

Z₁ (X₁, Х₂, Х₃, Х₄, Х₅) = Z₂ (X₁, Х₂, Х_З, Х₄, X₅) + Z₃ (X₁, Х₂, Х₃, Х₄, Х₅) +

+ Z₄ (X₁, Х₂, Х_З, Х₄, Х₅) + Z₅ (X₁, Х₂, Х_З, Х₄, Х₅) + Z₆ (X₁, Х₂, Х_З, Х₄, Х₅) = Х₁Х₄ + Х₁Х₂Х_З + Х₂Х₄ + Х₁Х_ЗХ₄ + Х₁Х₂Х_ЗХ₄.

Рисунок 2.17 - Дизъюнктивная ПЛМ на диодах

Рисунок 2.18 - Схема объединенной дизъюнктивной и конъюнктивной матриц

Рассмотрим матрицы, которые формируют прямые значения и их инверсии.

Конъюнктивная матрица (рис. 2.19)

Рисунок 2.19 - Схема конъюнктивной матрицы, формируемой простые и инверсные значения

Если на входе X_i(i = 1, 2, 3) U_bx = + Е, то диод будет закрыт и ток I от источника питания Е через R не течет. Падение напряжения на R отсутствуют и на вертикальной шине, соединенной с запертым диодом, остается высокий потенциал U_ВЫХ = + Е (лог.1). Если же U_bx = 0 (лог.0), то протекающий ток I создает на R падение U и U_ВЫХ = Е - IR = 0В.

Для сохранения на вертикальной шине матрицы M₁ высокого потенциала, необходимо, чтобы все диоды этой шины были заперты, т.е. на всех входах была лог.1. Если хотя бы один из диодов окажется открытым (т.е. на его входе лог.0), то протекающий через него ток I создает падение на R и на выходе будет лог.0. Таким образом, на вертикальной шине реализуется операция И от аргументов, помеченных крестиками. В примере (рис.2.19)

P₁ (Х₁Х₂Х₃) = _12З; Р₂ (Х₁Х₂Х₃) = Х₁Х₃;

Р₃ (Х₁Х₂Х₃) = X₁₂; P₄ (Х₁Х₂Х₃) = ₁Х₂Х₃.

Дизъюнктивная матрица(рис. 2.20)

Рисунок 2.20 - Схема дизъюнктивной матрицы на транзисторах

Если на вертикальной шине высокий потенциал, то транзистор открыт и высокий потенциал + Е через него поступает на горизонтальную выходную шину U_ВЫХ Е. Если же U_ВХ = 0 В (лог.0), то транзистор закрыт и U_ВЫХ = 0. Очевидно, что если хотя бы один из транзисторов, соединенных с горизонтальной шиной, окажется отк­рытым (т.е. на входе лог.1), то через него высокий потенциал + Е поступает на выход, т.е. на выходе будет лог.1. Таким образом, на горизонтальной шине реализуется операция ИЛИ от входных переменных P_i(i = 1, 2, 3, 4), помеченных крестиками. Поэтому матрицу М₂ называют матрицей ИЛИ. В примере (рис.2.20):

Y₁(X₁X₂X₃) = P₁ (Х₁Х₂Х₃) + P₂ (Х₁Х₂Х₃) + P₃ (Х₁Х₂Х₃);

Y₂(X₁X₂X₃) = P₂ (Х₁Х₂Х₃) + P₄ (Х₁Х₂Х₃).

В ПЛМ выходы P_i матрицы М₁ соединяются с одноименными входами И матрицы М₂, в результате чего ПЛМ (рис. 2.20) реализует функции

Y₁(X₁X₂X₃) = _12З + ХХ₃ + X₁X₂;

Y₂(X₁X₂X₃) = X₁X₃ + X₂X₃.

Такие ПЛМ, состоящие из 2-х матриц, называют двухуровневыми (рис. 2.216) и обозначаются ПЛМ (S, t, q), где S - число входов, t -число выходов, q - число промежуточных шин. Очевидно, что на одной ПЛМ может быть реализована система булевых функций, представленных в произвольной ДНФ, удовлетворяющих условиям X ≤ S, y ≤ t и B ≤ q, где В – число различных элементарных конъюнкций в системе. Условное изображение таких ПЛМ приведено на рис. 2.21а.

Сложность ПЛМ оценивают информационной емкостью (общим числом пересечений горизонтальных в вертикальных шин обеих матриц), равной (2S + t)q, где 2 – учитывая прямые и инверсные значения переменных.

Например, ППЛМ 556 РТ 1, имеющая параметры S = 16, t = 8, q = 48, заключена в корпусе с 28 выводами, потребляет Р=1 Вт, t_зад = 50 нс. Буква П - программируется пользователем. Существует ПЛМ с памятью (S, t, q, r), где r – разрядность регистра памяти.

ПЛМ применяются в качестве управляющей памяти ЭВМ с микрокомандным управлением и для реализации сложных алгоритмов. Быстродействие устройств на основе ПЛМ выше, чем у микропроцессоров.

Рассмотрим особенности технической реализации комбинационных ПЛМ. Пусть необходимо синтезировать цифровое устройство, описываемое системой функций

Y₁(X₁X₂X₃) = Х123 + Х24;

Y₂(X₁X₂X₃) = 23Х4 + Х123; (2.7)

Y₃(X₁X₂X₃) = 2Х4 +23Х4.

Для матричной реализации этой системы потребуется ПЛМ, имеющая 4 входа, 3 выхода и 3 терма (X1, 2,3, Х2,4,2,3, Х4), т.е. ПЛМ (а = 4, в = 3, с = 3). На рис. 2.22 приведена схема ПЛМ, реа­лизующей систему функций (2.7).

Рисунок 2.21 - Двухуровневая матрица

В настоящее время применяются БИС с параметрами:

12 ≥ а > 24 Например; ППЛМ К1556РТ1 а = 16, b = 8, с = 48;

БИС 12 ≥ b > 24 КР556РТЗ с памятью а = 16, b = 8. с = 90;

48 ≥ c > 96 d = 6.

Рисунок 2.22 - Схема ПЛМ, реализующая систему функций

Наиболее полное воплощение принцип создания различных комбинационных автоматов на базе ИМС с матричной структурой получил в базовых кристаллах (БК). Базовый кристалл представляет собой совокупность регулярно расположенных на полупроводни­ковом кристалле фрагментов (ячеек) между которыми имеются свободные зоны для создания межсоединений. Такой кристалл является заготовкой, из которой можно сформировать различные устройства, задав тот или иной рисунок межсоединений Изготовление па основе БК матричных БИС (МАБИС), называют полузаказными БИС. Стоимость и изготовление МАБИС в 4-5 раз меньше, чем стоимость БИС. По виду обрабатываемой информации БК бывают цифровые, аналоговые и смешанные. При этом используют технологии ЭСЛ, ТТЛШ, КМОП и N МОП.

Наиболее быстродействующие из кремниевых БК являются БК ЭСЛ – 0,5-0,6 нс при 300-2500 ячеек в кристалле.

Повысить быстродействие до 0,2 нс и обеспечить радиационную стойкость, позволяют БК на основе арсенида галлия.

Проектирование БИС на основе БК осуществляют с помощью библиотеки готовых решений.

Использование БК представляет собой важное направление в создании цифровых систем.