2. СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ

2.1. Задача синтеза комбинационных схем

Логическая схема, выходные сигналы Z_q которой описываются системой логических функций Z_q = f_q (X₁, X₂,...X_n), где X_p - входные сигналы логической схемы, p = 1, 2,..., n, q = 1, 2,..., k, называется комбинационной схемой (КС).

Общей задачей структурного синтеза является построение комбинационных схем, реализующих заданные алгоритмы, с помощью простых, называемых логическими элементами. В результате структурного синтеза должен быть определен перечень логических элементов, входящих в схему, и порядок их соединения между собой.

При синтезе комбинационных схем входные сигналы отождествляются с аргументами функции, а выходные сигналы - со значениями функции на тех или иных наборах входных сигналов.

Номенклатура выбранных элементов должна обладать функциональной полнотой, т.е. данная номенклатура элементов должна позволять строить любую сколь угодно сложную логическую схему.

Последовательность синтеза комбинационных схем состоит из следующих этапов:

формализация словесного задания;

составление таблицы истинности;

запись логической функции в СДНФ или СКНФ;

выбор функционально-полной системы логических элементов;

минимизация логической функции;

построение комбинационной схемы, соответствующей логической функции;

проверка правильности работы схемы.

При синтезе комбинационных схем формализация словесного задания обычно не вызывает затруднений и сводится к выявлению наборов переменных, на которых функция равна 1 или 0.

После этого стандартным способом записывается таблица истинности. В некоторых случаях задание определяет функцию не на всех наборах, что может быть использовано для последующего упрощения функции на этапе ее минимизации.

Доопределение не полностью определенных функций уже нами рассмотрено.

Выполнение операций третьего этапа основано на использовании правил составления СДНФ или СКНФ.

Обоснование выбора функционально-полной системы элементов определяется наличием элементов. Мы будем использовать основную систему логических элементов И, ИЛИ, НЕ.

Далее производится минимизация одним из рассмотренных методов. Построение комбинационной схемы по заданной логической функции включает в себя выполнение всех логических операций, указанных в выражении функции.

После построения схемы необходимо проверить правильность ее работы. При частичной проверке подают на вход схемы те наборы, на которых функция должна принять значения 0 или 1. Если выходные сигналы соответствуют этим значениям, то с большой вероятностью можно считать, что схема построена правильно. Более достоверной является полная проверка, при которой на схему подаются все 2ⁿ наборов и проверяется значение функции на выходе схемы.

Имея комбинационную схему, нетрудно выполнить обратную задачу: произвести анализ схемы с целью установления вида логической функции, которую она реализует. Для решения задачи анализа необходимо:

обозначить все выходные сигналы и все входные сигналы комбинационной схемы какими-либо буквами;

на выходе каждого элемента схемы отметить логическую функцию, реализуемую данным элементом, аргументами каждой функции являются сигналы, являющиеся входными для данного элемента, выполнение этого пункта целесообразно начинать со стороны входных сигналов;

логическая функция, записанная для элемента, выходным сигналом которого является исходный выходной сигнал комбинационной схемы, представляет собой логическую функцию комбинационной схемы, записанную для данного выходного сигнала. Для других выходных сигналов комбинационной схемы задача решается аналогичным образом.

Пример. Синтезировать комбинационную схему, запрещающую поступление на вход АСУ тетрад двоично-десятичного кода, у которых количество единиц в тетрадах больше двух (рис. 2.1).

Формализация словесного задания

В моменты поступления тетрад на выходе КС должен формироваться выходной сигнал равный 1, который запрещает прохождение этой тетрады на вход АСУ в случаях, если в тетраде содержится количество единиц больше двух, или равно двум, во всех остальных случаях - выходной сигнал должен быть равен 0.

Рисунок 2.1 - Связь КС с аппаратурой АСУ

Составление таблицы истинности

Таблица 2.1

Наборы	Т е т р а д ы				f(X,Y,Z,V)
	X	Y	Z	V
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1	0 0 0 1 0 1 1 0 0 1 1 1 1 1 1 1

Запись функции в сднф

Из таблицы 2.1 следует:

F(X, Y, Z, V) = ZV + YV + YZ + XV + XZ +

+ XZ + XY+XYV + XYZ + XYZV.

Синтез схемы проведем на элементах основного базиса И, ИЛИ, НЕ.

Минимизация логической функции.

Представим функцию в виде карты Карно.

Минимальная ДНФ имеет вид

F(X, Y, Z, V) = XY + YZ + XV + YZV + YZV + YZ.

Построение комбинационной схемы (рис. 2.2).

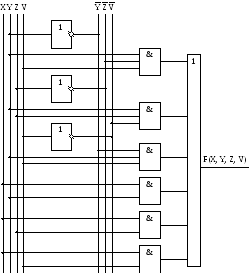
Рисунок 2.2 - Комбинационная схема в основном базисе

Синтез схемы в базисе “и-не”

Перейдем от ДНФ функции F(X, Y, Z, V) к ее представлению в базисе “И-НЕ”

F(X, Y, Z, V) = (X│Y) │ (X│Z) │ (X│V) │ (Y│Z│) │ (│Z│V) │ (Y││V).

На основании этого выражения построим логическую схему (рис.2.3).

Рисунок 2.3 - Комбинационная схема в базисе И - НЕ

Элементы, входящие в технический полный набор, выбранные для построения логической схемы, характеризуются, помимо прочего, коэффициентом объединения по входу m, коэффициентом разветвления по выходу n и задержкой сигнала Δ t3.

Интегрализация и унификация элементной базы приводят к необходимости ориентироваться на иные критерии оптимальности синтезируемых схем. Такими критериями могут быть: минимум количества интегральных микросхем, минимум коэффициента использования логических элементов в интегральных микросхемах, минимум выводов на разъемы и т.д. Такого рода критерии непосредственно связаны с задачами конструирования аппаратуры.

При решении задачи синтеза использовался критерий минимальности дизъюнктивных или конъюнктивных нормальных форм соответствующих переключательных функций, т.е. критерий минимума количества букв, входящих в эти формы. Однако этот критерий не всегда приводит к схемам, содержащим минимальное возможное количество элементов или деталей. Иногда удается упростить схему, если она построена по формулам, отличающимся от нормальных форм. В ряде случаев это можно сделать путем вынесения за скобки общих сомножителей или слагаемых соответственно в ДНФ и КНФ. При этом необходимо условиться о критерии оценки сложности схем. Сложность каждого элемента “И”, “ИЛИ”, “И-НЕ” и т.д. растет примерно пропорционально количеству его входов. Поэтому критерием сложности всей схемы может быть общее количество входов всех логических элементов, входящих в ее состав.

Пример. Пусть дана функция

f(X₁X₂X₃X₄) = X₁X₃X₄ + ₁X₂₃X₄ + X₁X₂X₃.

Эту функцию можно упростить, если вывести за скобки общий сомножитель X₁X₃ из первой и третьей конъюнкции. При этом получим следующее выражение:

f(X₁X₂X₃X₄) = X₁X₃ (X₄ + X₂) + ₁X₂₃X₄.

Общее число вхождений букв в полученную таким образом форму функции f(X₁X₂X₃X₄) равно 8, тогда как число вхождений букв в нормальную форму этой функции равно 10, т.е. при введении скобок и вынесении общего сомножителя за скобку получено дополнительно упрощение функции. Теперь в функции f(X₁X₂X₃X₄) конъюнкция X₁X₃ (X₄ + X₂) является сложной (в отличие от элементарных конъюнкций, входящих в нормальную форму, в которых отсутствуют скобки), так как в ней один из членов (X₄ + X₂), в свою очередь, является дизъюнкцией переменных X₄ и X₂. Формы, в которых встречаются скобки, называются скобочными формами булевых функций. Построим схемы, которые соответствуют формулам (нормальным и скобочным) (рис.2.4а,б).

При этом будем предполагать, что в распоряжении имеются как аргументы, так и их отрицания. Такая ситуация в дискретных системах имеет место, поскольку в качестве двоичных элементов памяти обычно используются триггеры, которые позволяют получать, как прямые, так и инвертированные сигналы.

Как видно из рис. 2.4а,б минимальная ДНФ функции приводит к более сложной схеме, чем скобочная форма. В первом случае общее число входов всех элементов равно 13, а во втором - 12.

а)

б)

Рисунок 2.4 - Комбинационные схемы в нормальных и скобочных формах

Необходимо отметить, что схемы, приведенные на рис. 2.4а,б, выдают выходные сигналы с разной задержкой. Так в схеме (рис. 2.4а), формирование выходного сигнала определяется временем задержки в 2-х последовательно соединенных логических элементах, а в схеме (рис. 2.4б) - в 3-х последовательно соединенных логических элементах.

Максимальное число последовательно выполненных логических операций для реализации функции f(X₁, X₂, ..., X_n) называется порядком логической функции.

Функции, представленные в любой нормальной форме, имеют порядок не выше второго.

Порядком или логической глубиной КС называется максимальное число последовательно включенных логических элементов. Порядки КС и соответствующие им функции совпадают.

На рис. 2.4а,б КС реализованы в соответствии с нормальной и скобочными формами, которые имеют порядок (логическую глубину), соответственно равным двум и трем, и максимальное число последовательно включенных логических элементов равно двум и трем, т.е. скобочные формы увеличивают порядок КС. Иначе эти КС называются, соответственно двухярусной или трехярусной.

Поскольку в каждом ярусе сигналы при прохождении элементов претерпевают задержку, то увеличение количества ярусов приводит к возрастанию задержки выходных сигналов по отношению к входным. Это снижает быстродействие логических схем, что во многих случаях является недопустимым. Поэтому, стремясь минимизировать логическую схему путем перехода к скобочным формам функции, необходимо всегда учитывать неизбежное уменьшение быстродействия схем.

Чем выше порядок КС, тем меньше ее быстродействие.

Скобочные формы представления логических функций используются для уменьшения стоимости КС. Так суммарное число входов логических элементов на рис. 2.4а равно 13, а на рис. 2.4б - 12. В общем случае стоимость КС и ее быстродействие жестко связаны. На практике очень часто используются КС, имеющие порядок выше десяти. В таких КС уменьшение быстродействия оправдывается существенным снижением стоимости их реализации.

Рассмотрим получение скобочных форм при минимизации КНФ.

Пример. Пусть имеется функция

f(X₁, X₂, X₃, X₄) = (X₁ + X₃ + X₄)( X₁ + X₂ + X₃)( X₁ + X₃ + ₄).

Легко видеть, что 1-я и 2-я дизъюнкции имеют общие слагаемые (X₁ + X₃).

Используя распределительный закон, перейдем к скобочной форме

f(X₁, X₂, X₃, X₄) = (X₁ + X₃ + X₄X₂)( X₁ + X₃ + X₄).

Первая форма имеет 9 вхождений переменных, а вторая - 7.

Скобочные формы могут содержать и большее число скобок, когда вынесение общих сомножителей за скобки производится последовательно несколько раз. Например, пусть упрощенная нормальная форма имеет вид

f(X₁, X₂, X₃, X₄) = X₃X₄ + X₂X₃X₄ + X₁X₂X₄ + X₁X₂X₄.

В начале, вынося общий сомножитель X₄ из 2-й, 3-й и 4-й конъюнкции, получим дизъюнкции.

Далее замечаем, что 1-й и 2-й члены дизъюнкции, заключенной в скобки, имеют общий сомножитель X₂. Вынося этот сомножитель за скобки, получим дизъюнкцию.

f(X₁, X₂, X₃, X₄) = X₃X₂ + X₄X₂(X₃ + X₁) + X₁X₂.

Первая форма имеет 11 вхождений переменных, а вторая - 8.

Итак, используя скобочные формы, можно минимизировать функцию.