4.3. Установление поля допуска.
Величина поля допуска обычно устанавливается по полученным значениям среднего и среднеквадратического параметра качества при выбранной двухсторонней вероятности α = 0,90; или α =0,95; или α= 0,99. Рекомендуется принимать значение величины поля допуска в пределах ±2 s. Установленное таким образом поле допуска следует нанести на ранее построенные графики (см. рис.2).
4.4. Расчет числа необходимых проверок при контроле качества.
Определение числа необходимых проверок при контроле качества сводится к планированию величины малой выборки nм для оценки среднего значения. Для этого следует задаться значением доверительной вероятности α = 0,90 или α =0,95 и предельной абсолютной ошибкой среднего ε. Величина абсолютной ошибки среднего может быть определена в долях от среднеквадратического – (0,3…1,0) s. Для выбранного значения доверительной вероятности и абсолютной ошибки среднего определяется величина s / ε, а по ней - величина малой выборки nм в функции от отношения s / ε по табл.9.
Таблица 9
Значение объема выборки nм в функции от соотношения s / ε
-
nм
α
nм
α
nм
α
0,90
0,95
0,90
0,95
0,90
0,95
2
1,167
1,390
7
0,620
0,739
12
0,475
0,566
3
0,950
1,130
8
0,581
0,692
13
0,455
0,543
4
0,822
0,980
9
0,548
0,653
14
0,440
0,524
5
0,734
0,874
10
0,520
0,620
15
0,425
0,506
6
0,671
0,800
11
0,495
0,590
20
0,365
0,438
Значение предельной абсолютной ошибки среднего ε наносится на график плотности вероятности (см. рис.2). Если значение малой выборки размером nм попадает внутрь этих границ, то среднее значение параметра, для оценки которого сделана малая выборка, совпадает со значением среднего x ср , определенного в п.4.1, с вероятностью α. Затем строится оперативная характеристика контроля, выражающая зависимость вероятности приемки всей партии изделий от значения выборочного среднего L (xср).
P (x ср) = 1- F0 |(c1 - x ср)| / s/ √ nм (15)
Значение c1 (приемочное число) принимается по нижней границе среднего, определяемой по формуле
c1= xн = xср – S t / √n (16)
При определении значения нижней границы xн величину t / √n для заданного в табл. 1 количества выполненных измерений принимаем равным 0,24. Значение F0 определяется из табл.7 для выбранной вероятности α (0,8 или 0,9).
Для построения оперативной характеристики значение x ср задается через 0,05 влево и вправо от c1. По трем полученным значениям P (x ср) строится опративная характеристика контроля (рис. 4).
Оценка партии по величине x ср выполняется для двух уровней: x o (браковочный уровень) и x m (приемочный уровень), причем x o > x m . Полагая риск поставщика α1 равным 0,05, а риск заказчика β =0,20, находятся величины x o и x m из выражений
α1= 1- F0 ( x 0 - c1 ) / s/ √ nм (17)
β = 1- F0 ( c1- x m ) / s/ √ nм (18)
Найденные величины x o и x m наносятся на оперативную характеристику, определяется зона хорошего качества, браковочного качества и зона неопределенности.
L
(xср)
1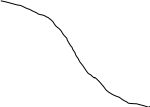
α1
хороший
уровень
зона неопределенности
β
брак
0
x m x o xср
Рис.4. Оперативная характеристика контроля