
- •5. Синтез і аналіз механізму привода
- •5.1. Задачі
- •5.2. Передаточне відношення
- •5.3. Синтез планетарного редуктора
- •5.4. Кінематичний аналіз привода
- •5.5. Геометричний синтез зубчастого зачеплення
- •5.6. Визначення розмірів зубчастого зачеплення
- •5.7. Побудова картини зачеплення
- •5.8. Визначення якісних показників зачеплення
5.5. Геометричний синтез зубчастого зачеплення
Задача геометричного синтезу зубчастого зачеплення полягає у визначенні його розмірів та якісних характеристик, залежних від геометрії зачеплення (коефіцієнта перекриття, відносного ковзання, питомого тиску).
Розміри зубчастих коліс, а також всього зачеплення, залежать від кількості зубців коліс, модуля зачеплення, загального для обох коліс, а також виду зачеплення.
В данному курсовому проекті розглядається рівнозміщене зачеплення. Рівнозміщене зачеплення складається з шестерні та колеса, нарізаних із зміщеннями, однаковими за модулем, але протилежними за знаком. Шестерня повинна бути додатним колесом, оскільки має меншу кількість зубців, більшу частоту обертання (зубці зазнають більшу кількість циклів навантаження), колесо має бути від’ємним.
5.6. Визначення розмірів зубчастого зачеплення
Розглянемо
зачеплення коліс 1
та 2.
Зачеплення рівнозміщене за умовою.
Шестернею є колесо 1.
Тоді коефіцієнт зміщення шестерні
![]() ,
колеса:
,
колеса:
![]() :
:
![]() ;
;
![]() .
.
Розрахунок проводимо наступним чином:
1.
Використовуючи таблиці
[2],
вибираємо коефіцієнти зміщення
та
![]() за числом зубців коліс
за числом зубців коліс
![]() та
та
![]() :
:
![]() ;
;
![]() .
.
2. Крок зачеплення по ділильному колу:
![]() .
.
3. Радіуси ділильних кіл:
шестерні
![]() ;
;
колеса
![]() .
.
4. Радіуси основних кіл:
шестерні
![]() ;
;
колеса
![]() ,
,
де
![]() – профільний кут інструментальної
рейки для нарізування зубів.
– профільний кут інструментальної
рейки для нарізування зубів.
5. Товщини зубців по ділильних колах:
шестерні
![]() ;
;
колеса
![]() .
.
6. Радіуси кіл западин:
шестерні
![]() ;
;
колеса
![]() ,
,
де
![]() – коефіцієнт висоти голови зуба та
– коефіцієнт висоти голови зуба та
![]() –
коефіцієнт радіально зазору – параметри
інструментальної рейки (за ГОСТ 13755 –
81).
–
коефіцієнт радіально зазору – параметри
інструментальної рейки (за ГОСТ 13755 –
81).
7. Міжосьова відстань:
![]() .
.
8. Радіуси початкових кіл дорівнюють радіусам ділильних кіл, тобто:
![]() ;
;
![]() .
.
9. Глибина заходу зубців:
![]() .
.
10. Висота зубця:
![]() .
.
11. Радіуси кіл виступів:
![]() ;
;
![]() .
.
12. Перевіряємо правильність розрахунків за допомогою формули:
![]() ;
;
![]() ;
;
![]() .
.
Рівність виконується, отже розрахунок проведений вірно.
5.7. Побудова картини зачеплення
Побудову проводимо у масштабі
![]()
Побудову картини зачеплення проводимо в наступній послідовності:
Відкладаємо на довільній прямій міжосьову відстань
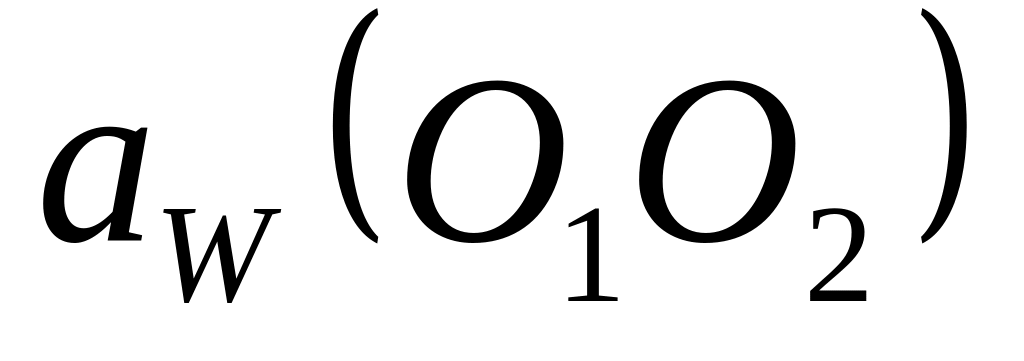 .
.З центрів обертання коліс О1 та О2 проводимо радіусами
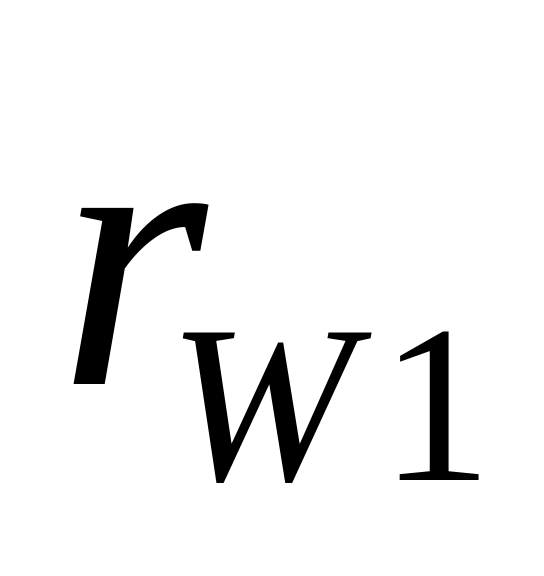 та
та
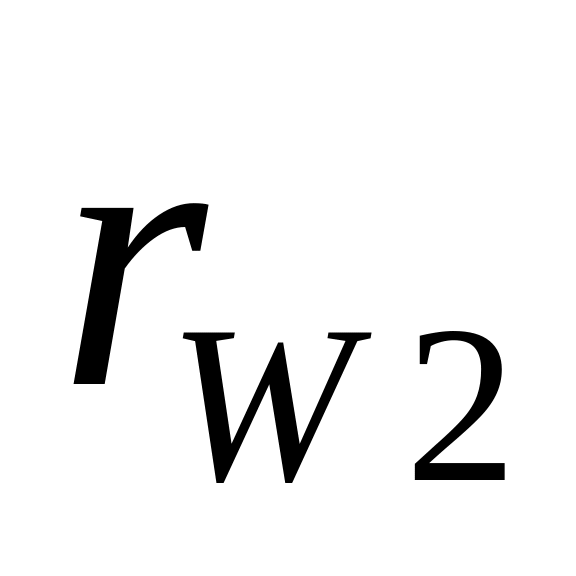 початкові кола. Вони дотикаються в
полюсі зачеплення Р.
початкові кола. Вони дотикаються в
полюсі зачеплення Р.Через полюс Р проводимо спочатку дотичну
 до початкових кіл, а потім під кутом
зачеплення
до початкових кіл, а потім під кутом
зачеплення
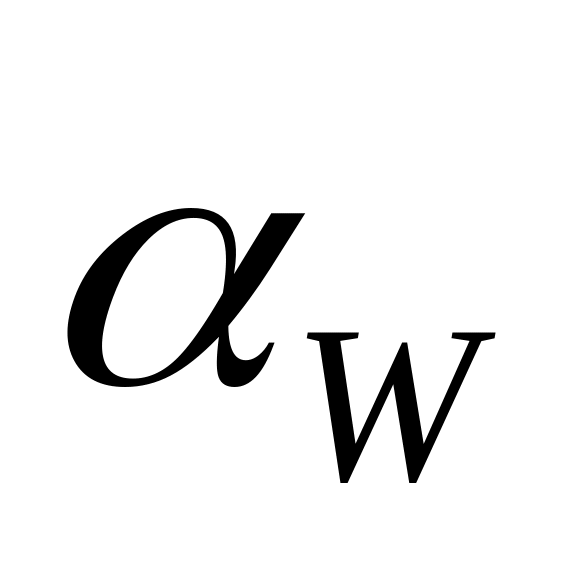 –
лінію зачеплення. Оскільки зачеплення
рівнозміщене, то кут зачеплення дорівнює
профільному куту рейки, тобто
–
лінію зачеплення. Оскільки зачеплення
рівнозміщене, то кут зачеплення дорівнює
профільному куту рейки, тобто
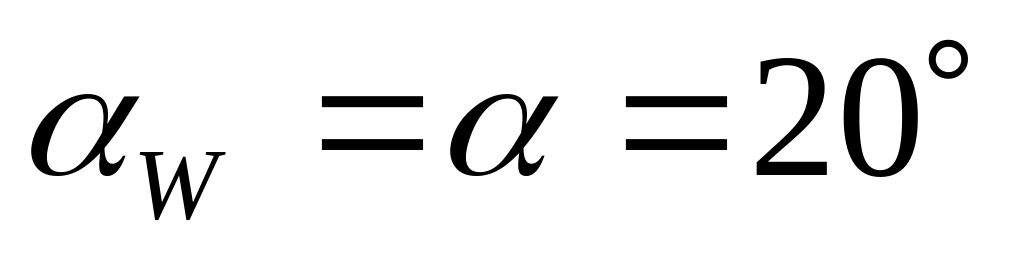 .
.Із центрів О1 та О2 проводимо перпендикуляри до лінії зачеплення і позначаємо точки N1 та N2. N1N2 – теоретична лінія зачеплення. Проводимо основні кола радіусами O1N1 та O2N2.
Будуємо евольвенти, які описує точка Р прямої N1N2 при перекочування її по основних колах.
Для
цього ділимо відрізок на 4 рівні частини
і за точкою відкладаємо 4 такі ж відрізки
– точки 1,
2, 3 ... 8.
Переносимо ці точки на основне коло
так, щоб одержувані дуги дорівнювали
відповідним частинам відрізка РN1.
Через одержані точки поділу дуги
основного кола
![]() проводимо
дотичні до нього і на них відкладаємо
відрізки, які містять у собі відповідну
кількість частин поділу відрізка РN1.
Знайдені точки з’єднуємо плавною кривою
і одержуємо евольвенту, яку вважаємо
профілем зуба шестерні. Аналогічно
будуємо евольвенту для колеса.
проводимо
дотичні до нього і на них відкладаємо
відрізки, які містять у собі відповідну
кількість частин поділу відрізка РN1.
Знайдені точки з’єднуємо плавною кривою
і одержуємо евольвенту, яку вважаємо
профілем зуба шестерні. Аналогічно
будуємо евольвенту для колеса.
Будуємо коло виступів обох коліс радіусами
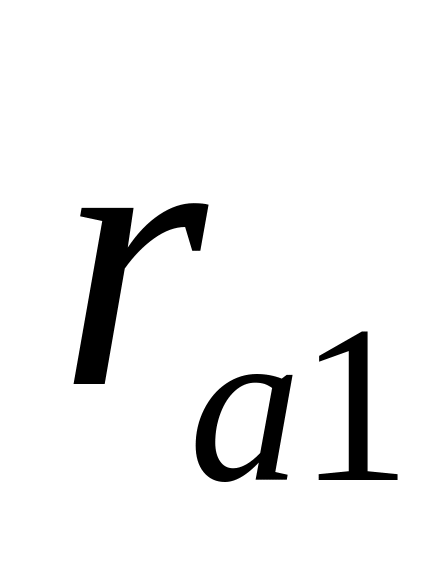 та
та
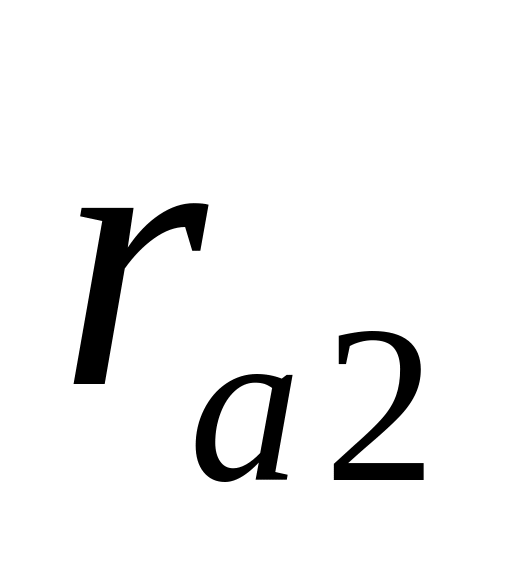 .
Перетин цих кіл з відповідними
евольвентами визначає крайні точки
профілів головок зубів.
.
Перетин цих кіл з відповідними
евольвентами визначає крайні точки
профілів головок зубів.Будуємо кола западин коліс. Від точки основи евольвенти до кола западин проводимо радіальний відрізок і заокруглюємо його дугою радіуса
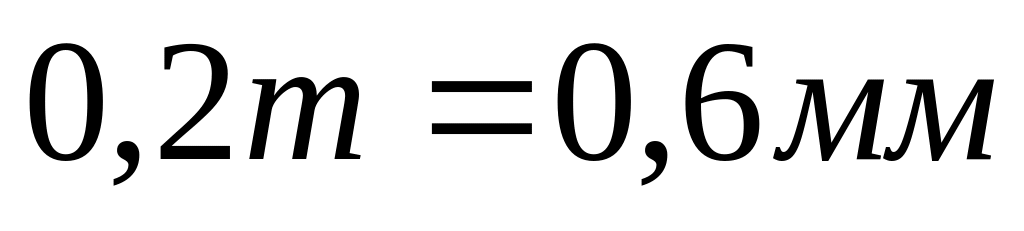 .
.Згідно з завданням, зачеплення рівнозміщене, то ділильні кола співпадають з початковими колами
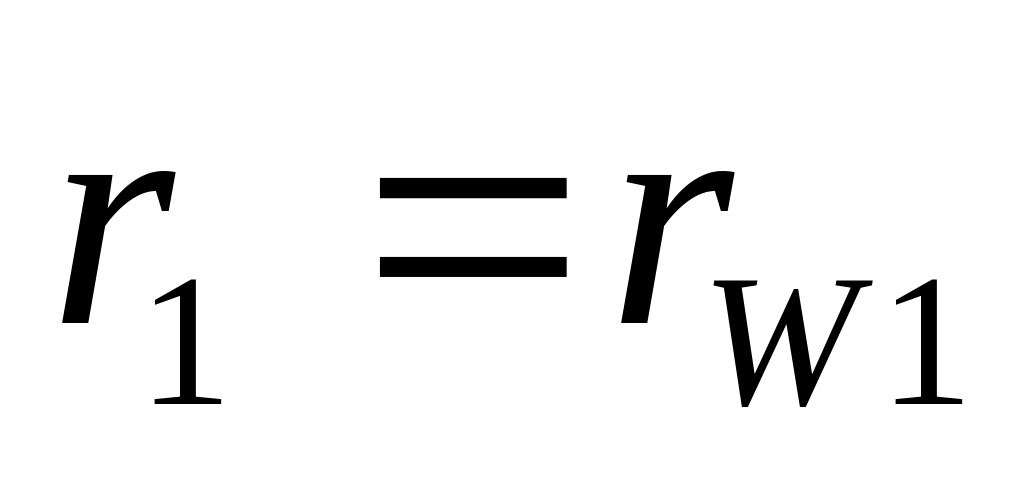 ,
,
 .
Від точки перетину ділильного кола
шестерні з евольвентною частиною
профілю відкладаємо по цьому колу
половину товщини зубця шестерні;
отриману точку з’єднуємо штриховою
лінією з центром О1
(отримуємо вісь симетрії зубця шестерні).
Таким чином, отримуємо половину зубця
шестерні.
.
Від точки перетину ділильного кола
шестерні з евольвентною частиною
профілю відкладаємо по цьому колу
половину товщини зубця шестерні;
отриману точку з’єднуємо штриховою
лінією з центром О1
(отримуємо вісь симетрії зубця шестерні).
Таким чином, отримуємо половину зубця
шестерні.
Будуємо симетрично другу половину зубця шестерні. Від осі симетрії одержаного зубця по ділильному колу відкладаємо крок зачеплення р і будуємо інші зубці шестерні.
Аналогічно будуємо профіль другого зубчастого колеса.
На кресленні необхідно також зобразити активну лінію та ділянки зачеплення. Активною лінією зачеплення називається відрізок АВ теоретичної лінії зачеплення N1N2 , який міститься між точками її перетину з колами виступів коліс.
АВ – це геометричне місце точок зачеплення (дотикання) спряжених профілів зубців на нерухомій площині.
Ділянки профілів зубців, які беруть участь у зачеплення називаються активними. Щоб знайти ці ділянки, треба через крайню точку А активної лінії зачеплення провести дугу радіуса О1А до перетину з профілем зубця першого колеса (точка а1) і через точку В провести дугу радіуса О2В до перетину з профілем зубця другого колеса (точка b2). Ділянка від вершини зубця до одержаної точки а1 на профілі зубця є його активною ділянкою, аналогічно для другого колеса активною ділянкою профілю зубця є ділянка між вершиною зубця цього колеса і точкою b2. Виділяємо на кресленні ці ділянки, проводячи паралельно профілю зубців на відстані 2 мм лінії й заштриховуємо одержані області.
Кожну з дуг початкових кіл, які перекочуються одна по одній за час зачеплення однієї пари спряжених профілів, називають дугою зачеплення. Для побудови дуг зачеплення потрібно:
через крайні точки а1 та b2 активної ділянки профілю першого колеса провести в напрямку вогнутості нормалі до цього профілю;
знайти точки
 та
та
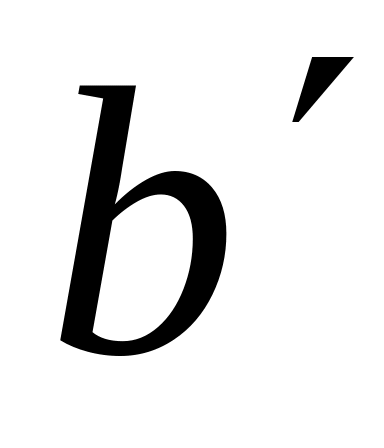 перетину цих нормалей з початковим
колом першого колеса.
перетину цих нормалей з початковим
колом першого колеса.дуга
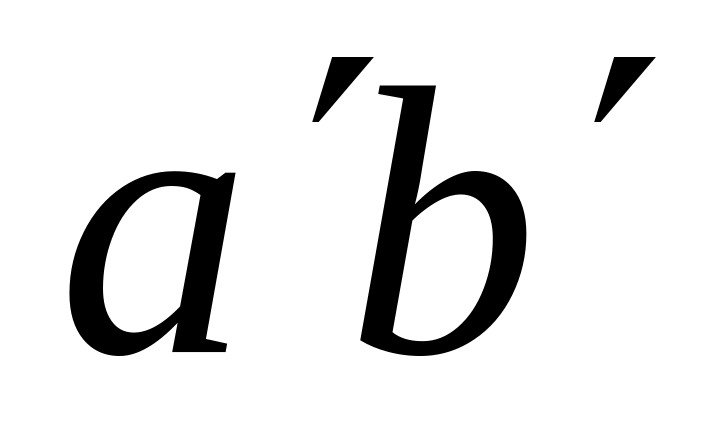 є дугою зачеплення на початковому колі
першого колеса.
є дугою зачеплення на початковому колі
першого колеса.
Аналогічно
будуємо дугу зачеплення
![]() на початковому колі другого колеса.
на початковому колі другого колеса.
Довжина дуги зачеплення визначається за формулою [3]:
![]() ,
,
де
![]() – довжина активної частини лінії
зачеплення,
– кут зачеплення.
– довжина активної частини лінії
зачеплення,
– кут зачеплення.
Довжину відрізка визначаємо з креслення:
![]()
Тоді, з урахуванням масштабу:
![]()
Звідки:
![]()
