6. Определение положения центра тяжести

Будем считать модель сплошной и однородной, состоящей из трех составных частей: носовой части [1], центральной [2] и кормовой [3] (весом оперения пренебрегаем).

Найдём положения центров тяжести и масс составных частей осесимметричного тела.

Имеем для усеченного конуса:

Плотность 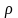будем считать постоянной

М асса усечённого конуса:

Момент массовых сил относительно начала координат (точки О):

Рис.3. Усеченный конус

О тсюда координата центра тяжести усеченного конуса:

Вычисление интегралов

,

О бозначим ,

Тогда:

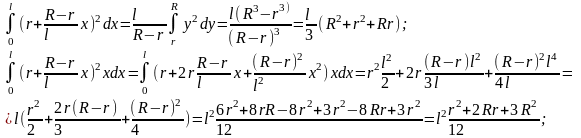
Будем считать модель сплошной и однородной, состоящей из трех составных частей: носовой части [1], центральной [2] и кормовой [3] (весом оперения пренебрегаем).

Д ля круглого прямого усеченного конуса масса m и положение центра тяжести x_ц.т. определяются соотношениями:

,

.

Для полного конуса (носовой части) r=0:

Для цилиндра (r=R):

Положение центра тяжести модели x₀ определяется по формуле:

, (24)

где

Разделив соотношение (24) на V₁, получим:

(25)

где

Хо=334.3

7. Расчет x_д – расстояния вдоль оси между центром тяжести и центром давлен

x_д=x_c-x_o,

x_c=H₁+l₁+AC.

Результаты сведем в таблицу 6.

Таблица 6

Расстояние между центром массы тела и центром давления.

α, [град]	0°	4°	8°	12°
Xд, мм	78.08	56.46	72.06	84.46

Зависимость X_д= X_д (α)

8. Вычисление коэффициента C_mz.

где

α град	0	4	8	12
Cmz	0	0.003	0.144	0.315

где угол α при вычислении производной берется в радианах.

Зависимость С_y=С_y(C_x) – поляра