Алгоритм Бойера — Мура
Данный алгоритм был разработан двумя учеными — Робертом Бойером (англ. Robert Stephen Boyer) и Джеем Муром (англ. J Strother Moore) в 1977 году. Он считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке.
Примечание:
Вопрос: что значит алгоритмы «общего назначения»?
Ответ: это значит, что эти алгоритмы универсальны, т.е. предназначены для решения широкого класса задач.
Ключевые понятия:
Алфавит — конечное множество символов.
Подстрока — это последовательность подряд идущих символов в строке.
Строка — последовательность символов текста.
Суффикс — это подстрока, заканчивающаяся на последний символ строки.
Примечание:
В определении строки речь не обязательно должна идти именно о тексте.
В общем случае строка — это любая последовательность байтов.
Поиск подстроки в строке осуществляется по заданному образцу, т. е. некоторой последовательности байтов, длина которой не превышает длину строки.
Наша задача заключается в том, чтобы определить, содержит ли строка заданный образец.
Описание:
Алгоритма Бойера — Мура можно представить в виде двух простых шагов.
1 шаг
Для искомого образца строим две таблицы — таблицу стоп-символов и таблицу суффиксов.
Примечание:
Процесс построения таблиц будет описан ниже.
2 шаг
Совмещаем начало строки и образца и начинаем проверку с последнего символа образца.
Если символы совпадают, производится сравнение предпоследнего символа образца и т. д. Если все символы образца совпали с наложенными символами строки, значит, подстрока найдена и поиск окончен.
Если же какой-то символ образца не совпадает с соответствующим символом строки, образец сдвигается на несколько символов вправо, и проверка снова начинается с последнего символа.
Назовем эти «несколько символов», упомянутые в предыдущем абзаце, величиной сдвига.
В качестве величины сдвига берется большее из двух значений:
1) Значение, полученное с помощью таблицы стоп-символов по простому правилу:
Если
несовпадение произошло на позиции
,
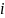а стоп-символ «
»,
то значение величины сдвига будет
равно
.
Примечание:
- позиция символа в образце (нумерация с 1);
— значение, записанное в таблице
стоп-символов, для символа «c».
2) Значение, полученное из таблицы суффиксов.
Подробное описание работы алгоритма
Псевдокод: алгоритм Бойера — Мура
Boyer-Moore-Matcher(
)
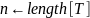
m
Compute-Last-Occurrence-Function(
)
Compute-Good-Suffix-Function(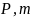
)
while
do
while
and
do
if
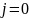
then print «Образец входит со сдвигом» s
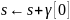
else
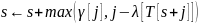
Алгоритм основан на трёх идеях.
1. Сканирование слева направо, сравнение справа налево.
Совмещается начало текста (строки) и шаблона, проверка начинается с последнего символа шаблона.
Если символы совпадают, производится сравнение предпоследнего символа шаблона и т. д.
Если все символы шаблона совпали с наложенными символами строки, значит, подстрока найдена, и поиск окончен.
Если же какой-то символ шаблона не совпадает с соответствующим символом строки, шаблон сдвигается на несколько символов вправо, и проверка снова начинается с последнего символа.
Примечание:
Эти «несколько», упомянутые в предыдущем абзаце, вычисляются по двум эвристикам.
Вопрос: что такое эвристика?
Ответ: эвристика — это не полностью математически обоснованный (или даже «не совсем корректный»), но при этом практически полезный алгоритм.
2. Эвристика стоп-символа (англ. bad-character heuristic).
Стоп-символ — это первый справа символ в строке, отличный от соответствующего символа в образце.
Эвристика стоп-символа предлагает попробовать новое значение сдвига, исходя из того, где в образце встречается стоп-символ (если вообще встречается).
В наиболее удачном случае стоп-символ выявляется при первом же сравнении и не встречается нигде в образце.
В
этом случае сдвиг можно сразу увеличить
на
:
любой меньший сдвиг заведомо не подойдет,
так как стоп- символ в тексте окажется
напротив какого-то символа из образца.
Если
этот наиболее удачный случай повторяется
постоянно, то при поиске подстроки мы
просмотрим всего лишь 
часть текста (вот как полезно сравнивать
справа налево!).
В
общем случае эвристика стоп-символа
работает так. Предположим, что при
сравнении права налево мы наткнулись
на первое несовпадение:
,
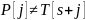где
.
Пусть
— номер самого правого вхождения
символа
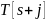в образец
(если этот символ вообще не появляется
в образце, считаем
равным
).
Мы утверждаем, что можно увеличить
на
,
не упустив ни одного допустимого сдвига.
В
самом деле, если
,
то стоп-символ
вообще не встречается в образце
,
так что можно сразу сдвинуть образец
на
позиций вправо.
Если
,
то образец можно сдвинуть на
позиций вправо, т.к. при меньших сдвигах
стоп-символ в тексте не совпадет с
соответствующим символом образца.
Наконец,
если
,
то эвристика предлагает сдвигать образец
не вправо, а влево; алгоритм Бойера —
Мура эту рекомендацию игнорирует,
поскольку эвристика безопасного суффикса
всегда предлагает ненулевой сдвиг
вправо.
Чтобы
применять эвристику стоп-символа полезно
для каждого возможного стоп-символа
вычислить значение
.
Это делается простой процедурой
Compute-Last-Occurrence-Function
(«найти последнее вхождение»), которая
для каждого
вычисляет
— номер крайнего правого вхождения
в
,
или нуль, если
в
не входит. В этих обозначениях приращение
сдвига, диктуемое эвристикой стоп-символа,
есть
,
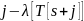как и написано в строке 13 алгоритма
Boyer-Moore-Matcher.
Псевдокод: найти последнее вхождение стоп-символа в подстроку
Compute-Last-Occurrence-Function( )
for each character
do
for
to
do
return
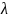
Примечание:
Время
работы
процедуры
Compute-Last-Occurrence-Function есть
Пример использования эвристики стоп-символа:
Предположим, что мы производим поиск слова «колокол».
Первая же буква не совпала — «к» (назовём эту букву стоп-символом).
Тогда можно сдвинуть шаблон вправо до последней буквы «к».
!
Строка: * * * * * * к * * * * * *
Шаблон: к о л о к о л
Следующий шаг: к о л о к о л
Если стоп-символа в шаблоне вообще нет, шаблон смещается за этот стоп-символ.
!
Строка: * * * * * а л * * * * * * * *
Шаблон: к о л о к о л
Следующий шаг: к о л о к о л
В данном случае стоп-символ — «а», и шаблон сдвигается так, чтобы он оказался прямо за этой буквой. В алгоритме Бойера — Мура эвристика стоп-символа вообще не смотрит на совпавший суффикс (см. ниже), так что первая буква шаблона («к») окажется под «л», и будет проведена одна заведомо холостая проверка.
Если стоп-символ «к» оказался за другой буквой «к», эвристика стоп-символа не работает.
!
Строка: * * * * к к о л * * * * *
Шаблон: к о л о к о л
Следующий шаг: к о л о к о л ?????
В таких ситуациях выручает третья идея алгоритма — эвристика совпавшего суффикса.
3. Эвристика безопасного (совпавшего) суффикса (англ. good-suffix heuristic).
Если
и
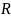— строки, будем говорить, что они сравнимы
(обозначение:
),
если одна из них является суффиксом
другой. Если выровнять две сравнимые
строки по правому краю, то символы,
расположенные один под другим, будут
совпадать. Отношение
симметрично: если
,
то и
.
Эвристика
безопасного суффикса состоит в следующем:
если
,
где
(и число
— наибольшее с таким свойством), то мы
можем безбоязненно увеличить сдвиг на
Иными
словами,
— наименьшее расстояние, на которое мы
можем сдвинуть образец без того, чтобы
какой- то из символов, входящих в
«безопасный суффикс»
оказался напротив несовпадающего с
ним символа из образца. Поскольку строка
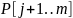заведомо сравнима с пустой строкой
,
число
корректно определено для всех
.
Стоит также заметить, что
для всех
,
так что на каждом шаге алгоритма Бойера
— Мура образец будет сдвигаться вправо
хотя бы на одну позицию. Мы будем называть
функцией
безопасного суффикса
(англ. good-suffix
function),
ассоциированной со строкой
.
Псевдокод: вычисление функции безопасных суффиксов
Compute-Good-Suffix-Function( )
m = length(P)
pi[] = префикс-функция(P)
pi1[] = префикс-функция(обращение(P))
for j=0..m
suffshift[j] = m - pi[m]
for i=1..m
j = m - pi1[i]
suffshift[j] = min(suffshift[j], i - pi1[i])
Примечание:
Время
работы процедуры Compute-Good-Suffix-Function
есть
.
Пример использования эвристики безопасного (совпавшего) суффикса:
Если при сравнении строки и шаблона совпало один или больше символов, шаблон сдвигается в зависимости от того, какой суффикс совпал.
Строка: * * т о к о л * * * * *
Шаблон: к о л о к о л
Следующий шаг: к о л о к о л
В данном случае совпал суффикс «окол», и шаблон сдвигается вправо до ближайшего «окол». Если подстроки «окол» в шаблоне больше нет, но он начинается на «кол», сдвигается до «кол», и т. д.
Обе эвристики требуют предварительных вычислений — в зависимости от шаблона поиска заполняются две таблицы. Таблица стоп-символов по размеру соответствует алфавиту (например, если алфавит состоит из 256 символов, то её длина 256); таблица суффиксов — искомому шаблону. Именно из-за этого алгоритм Бойера — Мура не учитывает совпавший суффикс и несовпавший символ одновременно — это потребовало бы слишком много предварительных вычислений.
Опишем подробнее обе таблицы.
Таблица стоп-символов
Считается, что символы строк нумеруются с 1 (как в Паскале).
В таблице стоп-символов указывается последняя позиция в образце (исключая последнюю букву) каждого из символов алфавита. Для всех символов, не вошедших в образец , пишем 0 (для нумерации с 0 — соответственно, −1).
Например,
если
,
таблица стоп-символов будет выглядеть
так.
Символ a b c d [все остальные]
Последняя позиция 5 2 7 6 0
Обратите внимание, для стоп-символа «d» последняя позиция будет 6, а не 8 — последняя буква не учитывается. Это известная ошибка, приводящая к неоптимальности. Для АБМ она не фатальна («вытягивает» эвристика суффикса), но фатальна для упрощённой версии АБМ — алгоритма Хорспула.
Если несовпадение произошло на позиции , а стоп-символ , то сдвиг будет .
Таблица суффиксов
Для
каждого возможного суффикса
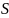шаблона
указываем наименьшую величину, на
которую нужно сдвинуть вправо шаблон,
чтобы он снова совпал с
.
Если такой сдвиг невозможен, ставится
(в обеих системах нумерации). Например,
для того же
будет:
Суффикс [пустой] d cd dcd ... abcdadcd
Сдвиг 1 2 4 8 ... 8
Иллюстрация
было ? ?d ?cd ?dcd ... abcdadcd
стало abcdadcd abcdadcd abcdadcd abcdadcd ... abcdadcd
Если шаблон начинается и заканчивается одной и той же комбинацией букв, вообще не появится в таблице.
Например,
для
для всех суффиксов (кроме, естественно,
пустого) сдвиг будет равен 4.
Суффикс [пустой] л ол ... олокол колокол
Сдвиг 1 4 4 ... 4 4
Иллюстрация
было ? ?л ?ол ... ?олокол колокол
стало колокол колокол колокол ... колокол колокол
Пример:
Пусть у нас
есть набор символов (алфавит) из
пяти символов:
и мы хотим найти вхождение образца “
”
в строке “
”.
Следующие схемы иллюстрируют все этапы
выполнения алгоритма:
1 шаг
Таблица стоп-символов
-
a
b
c
d
e
4
3
0
0
0
Если несовпадение произошло на позиции , а стоп-символ , то сдвиг будет .
Таблица суффиксов для образца “ ”.
Суффикс [пустой] d ad bad bbad abbad
Сдвиг 1 5 5 5 5 5
Иллюстрация
было ? ?d ?ad ?bad ?bbad abbad
стало abbad abbad abbad abbad abbad abbad
2 шаг
a b e c c a a b a d b a b b a d
a b b a d
Накладываем образец на строку. Совпадения суффикса нет — таблица суффиксов даёт сдвиг на одну позицию. Для несовпавшего символа исходной строки «с» (5-я позиция) в таблице стоп-символов записан 0. Сдвигаем образец вправо на 5-0=5 позиций:
a b e c c a a b a d b a b b a d
a b b a d
Символы 3—5 совпали, а второй — нет. Эвристика стоп-символа для «а» не работает (2-4=-2). Но поскольку часть символов совпала, в дело включается эвристика совпавшего суффикса, сдвигающая образец сразу на пять позиций!
a b e c c a a b a d b a b b a d
a b b a d
И снова совпадения суффикса нет. В соответствии с таблицей стоп-символов сдвигаем образец на 1 позицию и получаем искомое вхождение образца:
a b e c c a a b a d b a b b a d
a b b a d