[Править]Интегральная форма
При помощи формул Остроградского—Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
Название |
СГС |
СИ |
Примерное словесное выражение |
Закон Гаусса |
|
|
Поток электрической индукции через замкнутую поверхность sпропорционален величине свободного заряда, находящегося в объёме v, который окружает поверхность s. |
Закон Гаусса для магнитного поля |
|
|
Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют). |
Закон индукции Фарадея |
|
|
Изменение потока магнитной индукции, проходящего через незамкнутую поверхностьs, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре l, который является границей поверхности s. |
Теорема о циркуляции магнитного поля |
|
|
Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность s, пропорциональны циркуляции магнитного поля на замкнутом контуре l, который является границей поверхности s. |
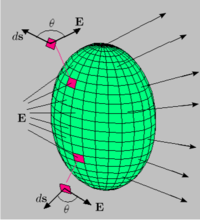
Поток электрического поля через замкнутую поверхность
Введённые обозначения:
—
двумерная
замкнутая в случае теоремы Гаусса
поверхность, ограничивающая объём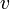 
,
и открытая поверхность в случае законов
Фарадея и Ампера — Максвелла (её границей
является замкнутый контур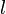 
).
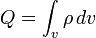— электрический
заряд,
заключённый в объёме
,
ограниченном поверхностью
(в
единицах СИ — Кл);
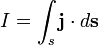— электрический
ток,
проходящий через поверхность
(в
единицах СИ — А).
При
интегрировании по замкнутой поверхности
вектор элемента площади 
направлен
из объёма наружу. Ориентация
при
интегрировании по незамкнутой поверхности
определяется направлениемправого
винта,
«вкручивающегося» при повороте в
направлении обхода контурного интеграла
по 
.
Словесное
описание законов Максвелла, например,
закона Фарадея, несёт отпечаток традиции,
поскольку вначале при контролируемом
изменении магнитного потока регистрировалось
возникновение электрического поля
(точнее электродвижущей
силы).
В общем случае в уравнениях Максвелла
(как в дифференциальной, так и в
интегральной форме) векторные
функции 
являются
равноправными неизвестными величинами,
определяемыми в результате решения
уравнений.
[Править]Сила Лоренца
Основная статья: Сила Лоренца
При
решении уравнений Максвелла распределения
зарядов
и
токов
часто
считаются заданными. С учётом граничных
условий и материальных
уравнений это
позволяет определить напряжённость
электрического поля
и
магнитную индукцию
,
которые, в свою очередь, определяют
силу, действующую на пробный заряд 
,
двигающийся со скоростью
.
Эта сила называется силой
Лоренца:
СГС |
СИ |
|
|
Электрическая
составляющая силы направлена по
электрическому полю (если 
),
а магнитная — перпендикулярна
скорости заряда и магнитной индукции.
Впервые выражение для силы, действующей
на заряд в магнитном поле (электрическая
компонента была известна), получил
в 1889
году Хевисайд[30][31] за
три года до Хендрика
Лоренца,
который вывел выражение для этой силы
в 1892
году.
В более сложных ситуациях в классической и квантовой физике в случае, когда под действием электромагнитных полей свободные заряды перемещаются и изменяют значения полей, необходимо решение самосогласованной системы из уравнений Максвелла и уравнений движения, включающих силы Лоренца. Получение точного аналитического решения такой полной системы сопряжено обычно с большими сложностями.