Аналоговая и цифровая фильтрация в среде matlab

Рассмотрим процесс линейной фильтрации на примере линейного стационарного фильтра, который в непрерывном времени описывается дифференциальным уравнением второго порядка:

(1)

где х — заданный процесс, подаваемый на вход этого фильтра, орядок фильтра определяется порядком уравнения; у — процесс, получаемый на выходе фильтра; - частота собственных колебаний фильтра, — относительный коэффициент затухания этого фильтра.

Передаточная функция фильтра, выраженная через комплексную частоту , имеет вид:

(2)

Для графического представления передаточной функции любого линейного фильтра в среде MATLAB удобно использовать процедуру freqs. В общем случае обращение к ней имеет вид:

h = freqs (b, a,w)

При этом процедура создает вектор h комплексных значений частотной характеристики по передаточной функции звена, заданной векторами коэффициентов ее числителя ) и знаменателя (а), а также по заданному вектору w частоты . Если вектор w не указан, процедура автоматически выбирает 200 отсчетов частоты, для которых вычисляется частотная характеристика.

Если не указана выходная величина, т.е. обращение имеет вид:

freqs (b,a,w)

процедура выводит в текущее графическое окно два графика, АЧХ и ФЧХ.

Рассмотрим пример.

Пусть для передаточной функции (2)

; ;

В приведенном фрагменте программы вычисляются значения коэффициентов числителя и знаменателя и выводятся графики АЧХ и ФЧХ:

%a_filtr

T0=1;dz=0.05;omO=2*pi/T0; A=1;

omO=2*pi/T0; A=1;

a1(1)=1;a1(2)=2*dz*omO;

a1(3)=om0^2;b(1)=A;

freqs(b,a1)

Результат выполнения программы приведен на рис 1.

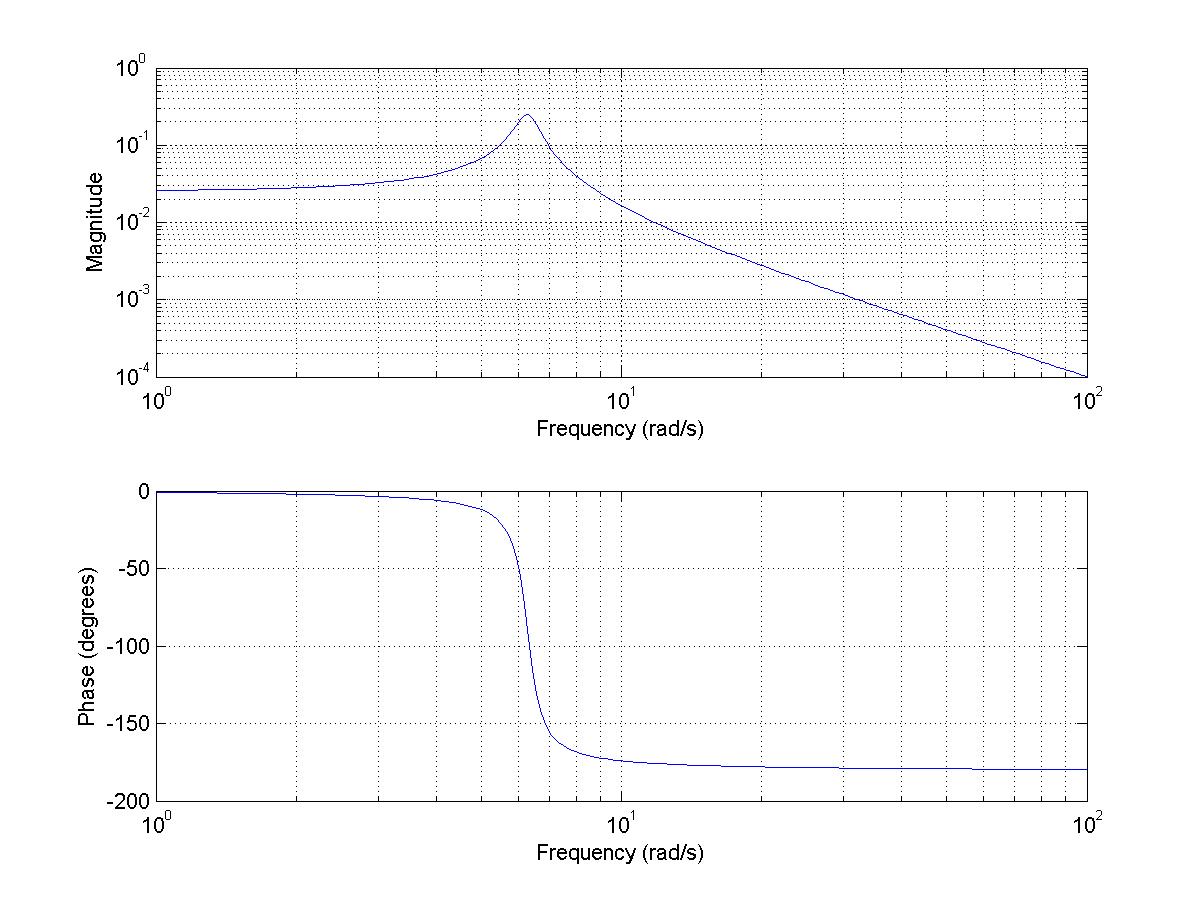
рис 1. АЧХ и ФЧХ фильтра второго порядка.

Группа функций freqs в общем выполняет расчет частотной характеристики по передаточной функции аналогового фильтра (преобразованию Лапласа импульсной характеристики), заданной векторами числителя и знаменателя:

(2)

Функция h=freqs(b,a,w) вычисляет значения частотной характеристики аналогового фильтра по отсчетам частоты, выраженным в радианах в секунду, которые задаются в векторе w.

Функция [h,w]=freqs(b,a) автоматически выбирает 200 частотных отсчетов, для которых вычисляется частотная характеристика. Число отсчетов может быть задано параметром n. В этом случае используется функция[h,w]=freqs(b,a,n).

Выполним вычисление и вывод частотной характеристики с передаточной функцией

Программа расчета может быть построена следующим образом:

%a_filtr2

a=[1 0.4 1];

b=[0.2 0.3 1];

w=logspace(-1,1);

freqs(b,a,w)

Результаты вычислений приведены на рис 2.

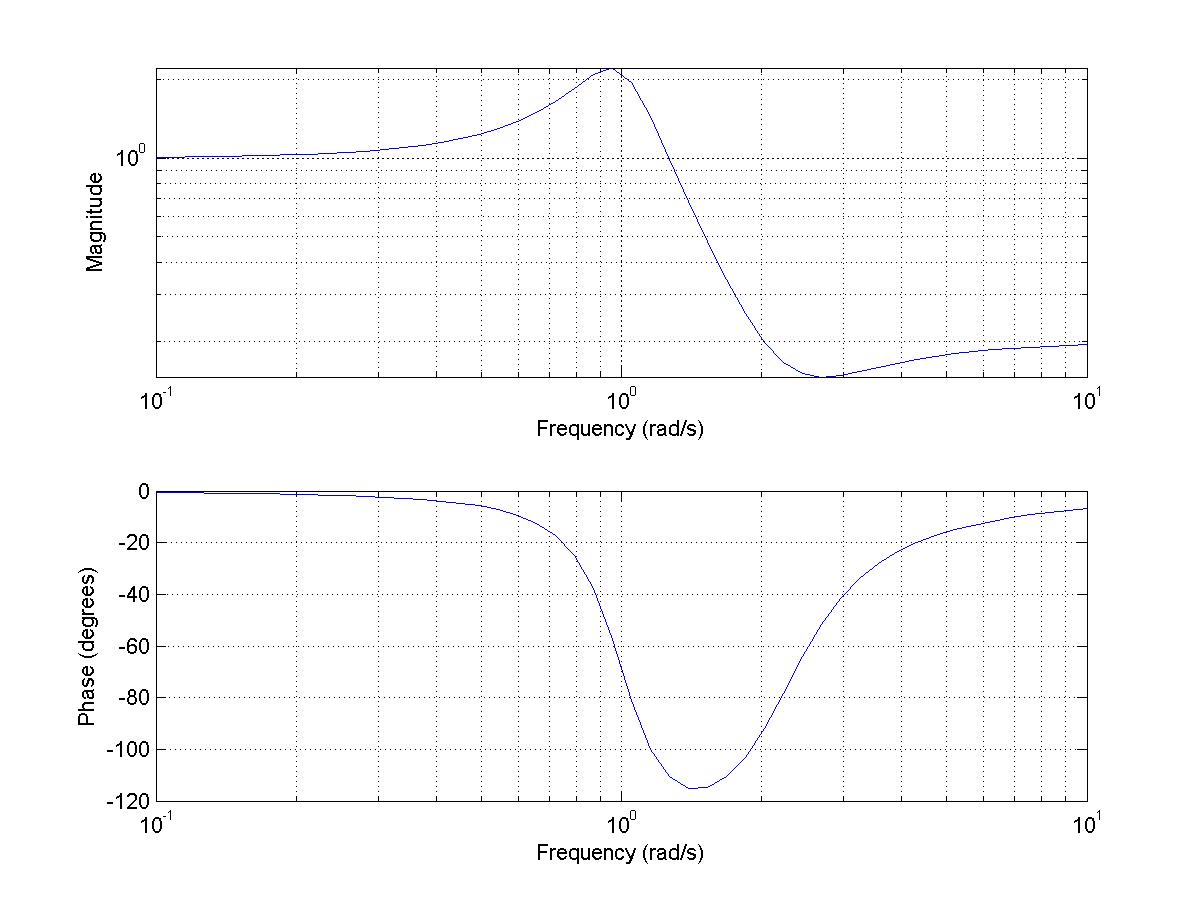
рис 2.

Входной процесс x(t) может быть представлен совокупностью дискретных отсчетов выбранных в моменты времени с одинаковым шагом (дискретом) Ts. Время принимает только дискретные значения t= k Ts. В этом случае входной процесс может быть представлен вектором значений x(k), где k –номер измерения с начала процесса. (t= k Ts).

В этом случае исходное дифференциальное уравнение может быть выражено через конечные разности переменных х и у. Конечно разностным эквивалентом производной является величина:

,

а второй производной , отношение

При этом дискретным аналогом дифференциального уравнения (1) будет разностное уравнение:

Применяя к полученному уравнению Z-преобразование, получим:

, (4)

где:

(5)

Дискретная передаточная функция фильтра определяется из уравнения (4):

(6)

Таким образом цифровым аналогом колебательного звена является цифровой фильтр с коэффициентами числителя и знаменателя, рассчитанными по формулам (4) и (5).

Чтобы получить частотную характеристику по дискретной передаточной, функции , заданной векторами значений ее числителя и знаменателя , используется процедура freqz, аналогичная freqs.

Фильтрация сигнала в пакете MATLAB с помощь линейного фильтра, описываемого передаточной функцией вида:

(7)

осуществляется процедурой filter следующим образом:

y=filter (b,a,x)

где х – заданный вектор значений входного сигнала; у- вектор значений выходного сигнала фильтра после процедуры фильтрации; b-вектор коэффициентов числителя дискретной передаточной функции (7) линейного фильтра; а-вектор коэффициентов знаменателя передаточной функции.

Рассмотрим пример задачи фильтрации. Пусть имеется сигнал синусоидальной формы с периодом Т1=1 (с) и амплитудой А1=0.75. Сформируем этот сигнал в виде вектора с периодом Т1=1 и амплитудой А1=0.75. Вектор значений сигнала определен в дискретные моменты времени с шагом Ts=0.001:

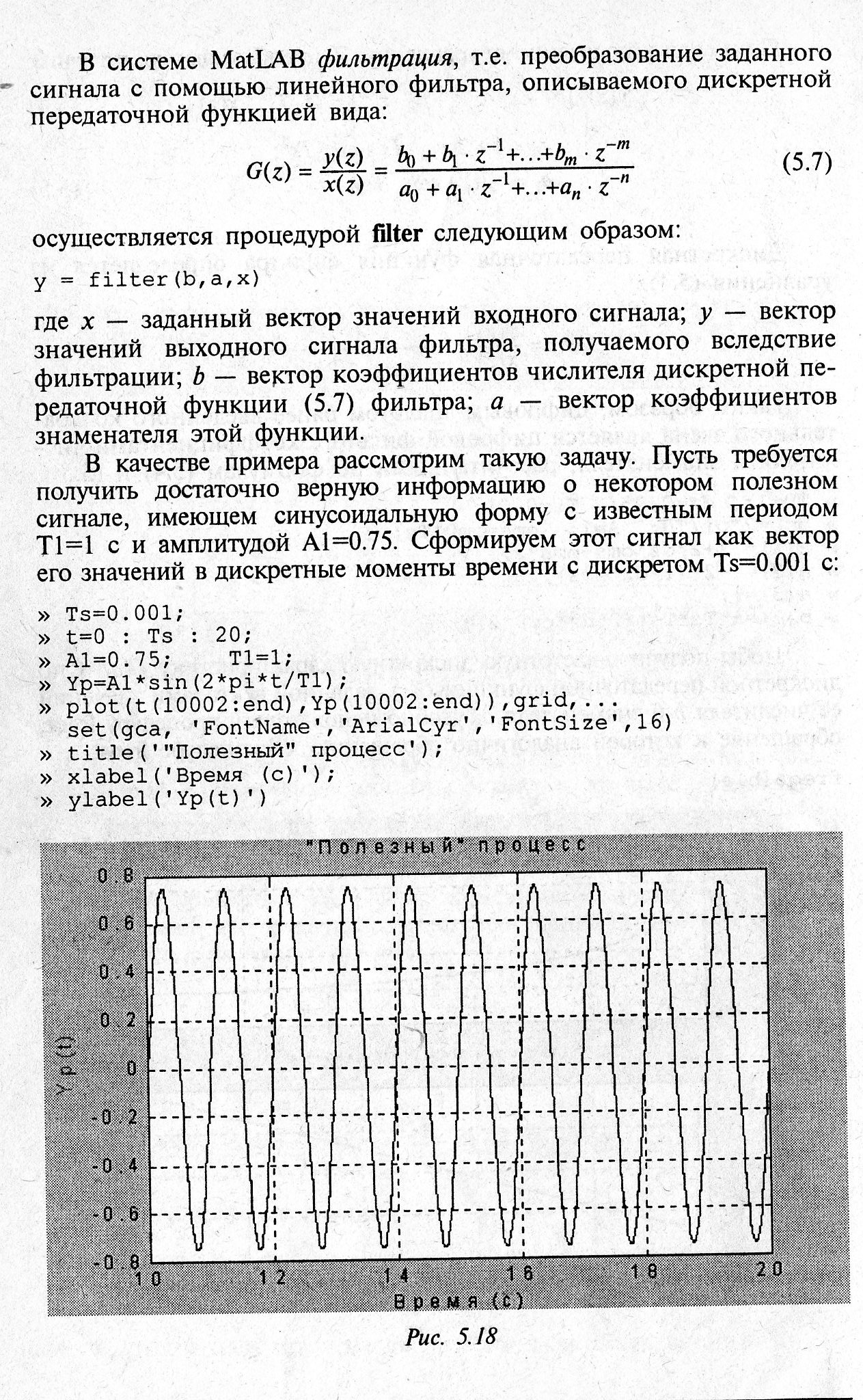
Пусть в процессе обработки сигнала (первичным преобразователем) к полезному сигналу добавился шум, представляющий собой высокочастотную синусоиду с периодом и амплитудой , а в процессе измерения – гауссовый шум измерителя с интенсивностью . Измеренный сигнал после измерения будет иметь вил:

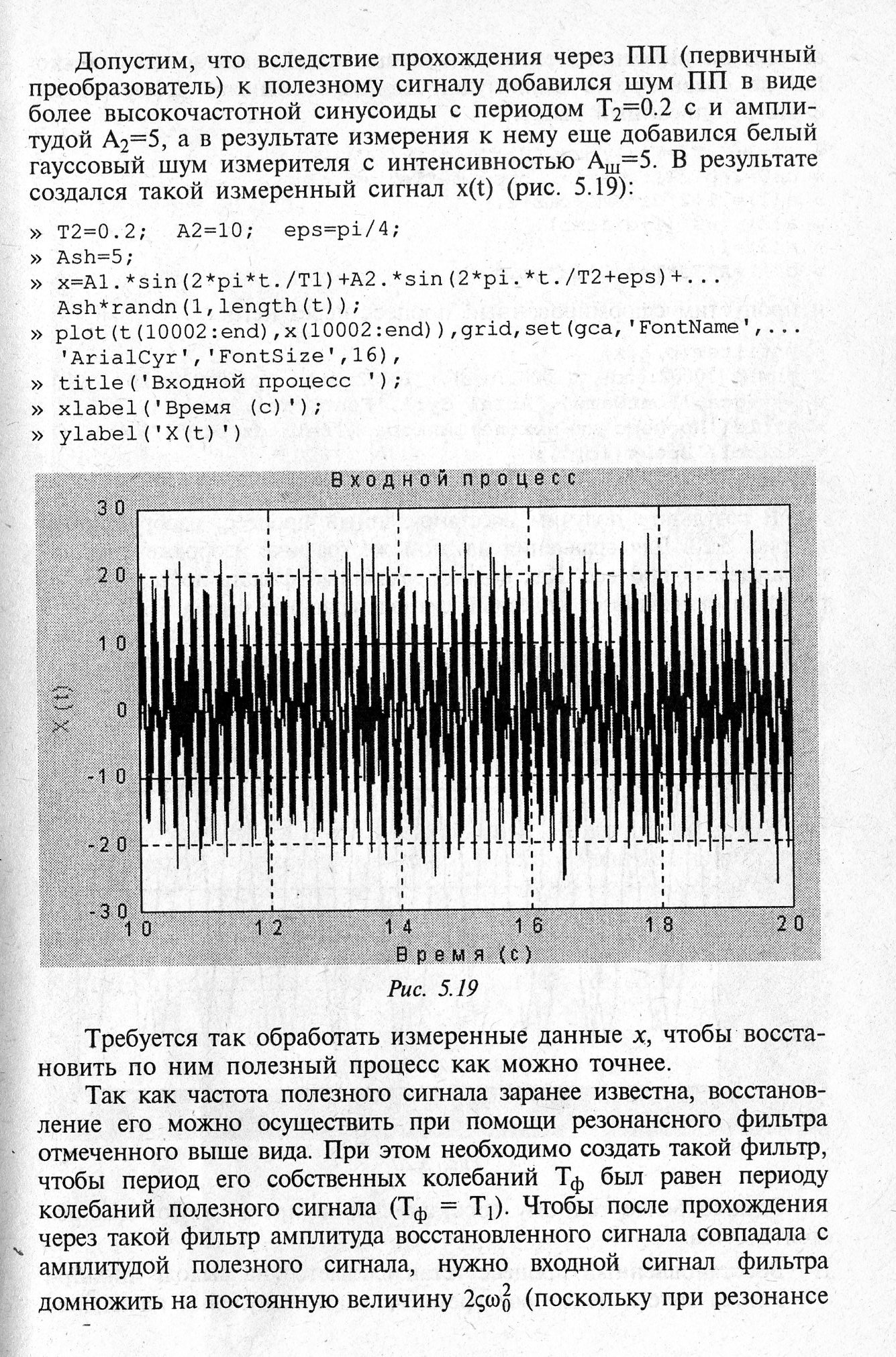
График сигнала после измерения приобретет вид:

Рис 3.

Задачей обработки измерений является возможно более полное восстановление полезного сигнала на фоне аддитивных добавок помех и шумов. Поскольку частота полезного сигнала известна, задача может быть решена посредством линейной фильтрации. Вследствие монохроматичности полезного сигнала в качестве линейного фильтра можно применить резонансный фильтр. Резонансная частота такого фильтра должна быть обратно пропорциональна периоду колебаний полезного сигнала, а для восстановления амплитуды полезного сигнала амплитуда входного сигнала фильтра домножается на постоянную величину , поскольку при резонансе изменение амплитуды сигнала по сравнению с входным сигналом пропорционально этой же величине. Программа фильтра имеет вид

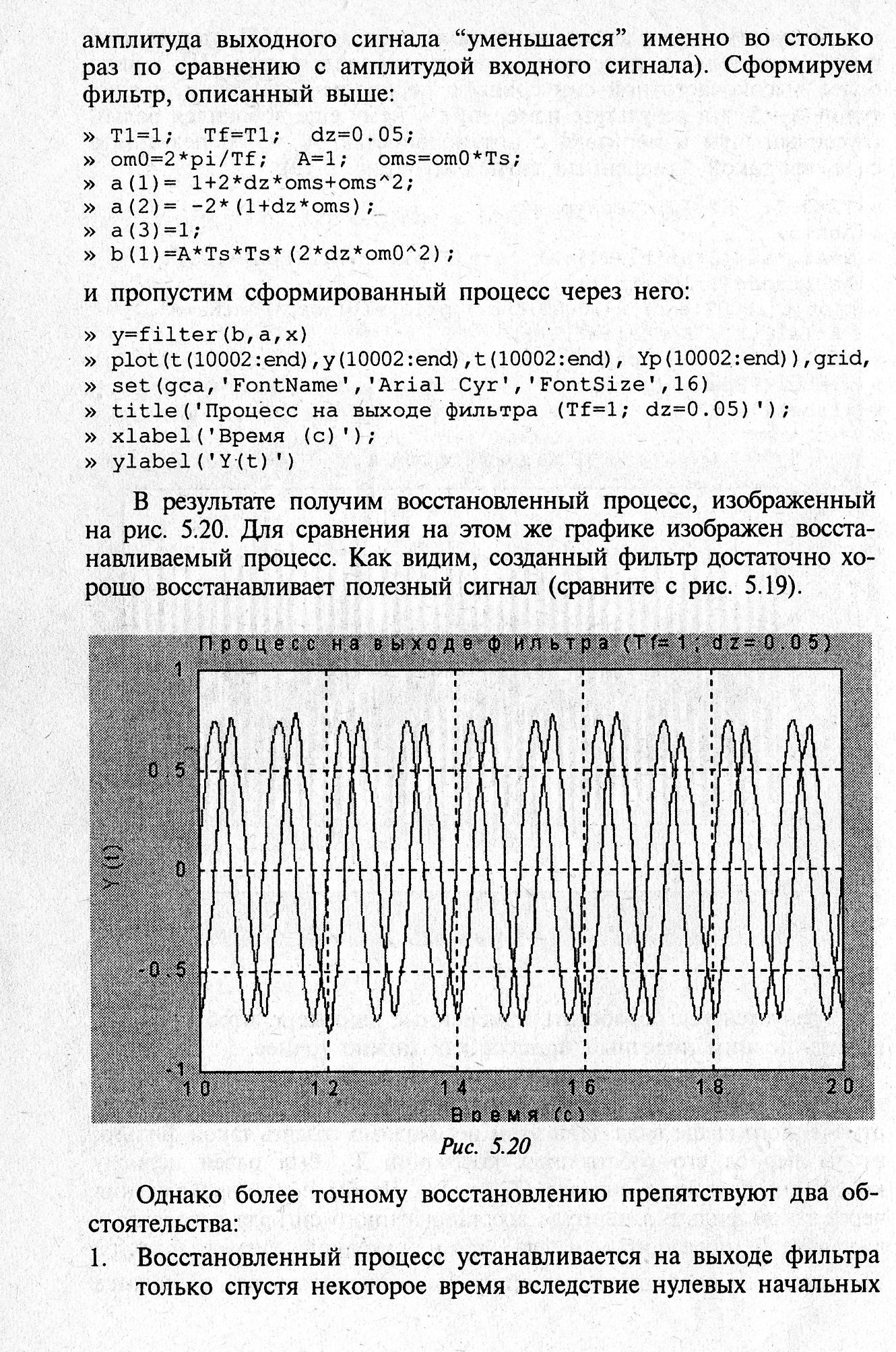
В результате получим восстановленный процесс, рис 4. Для сравнения на рис 4 показан исходный сигнал. Созданный фильтр достаточно хорошо восстанавливает полезный сигнал.

Рис.4

Более точному восстановлению препятствуют 2 обстоятельства:

1. восстановленный процесс устанавливается с запозданием вследствие нулевых начальных условий самого фильтра, как динамического звена, рис 5.

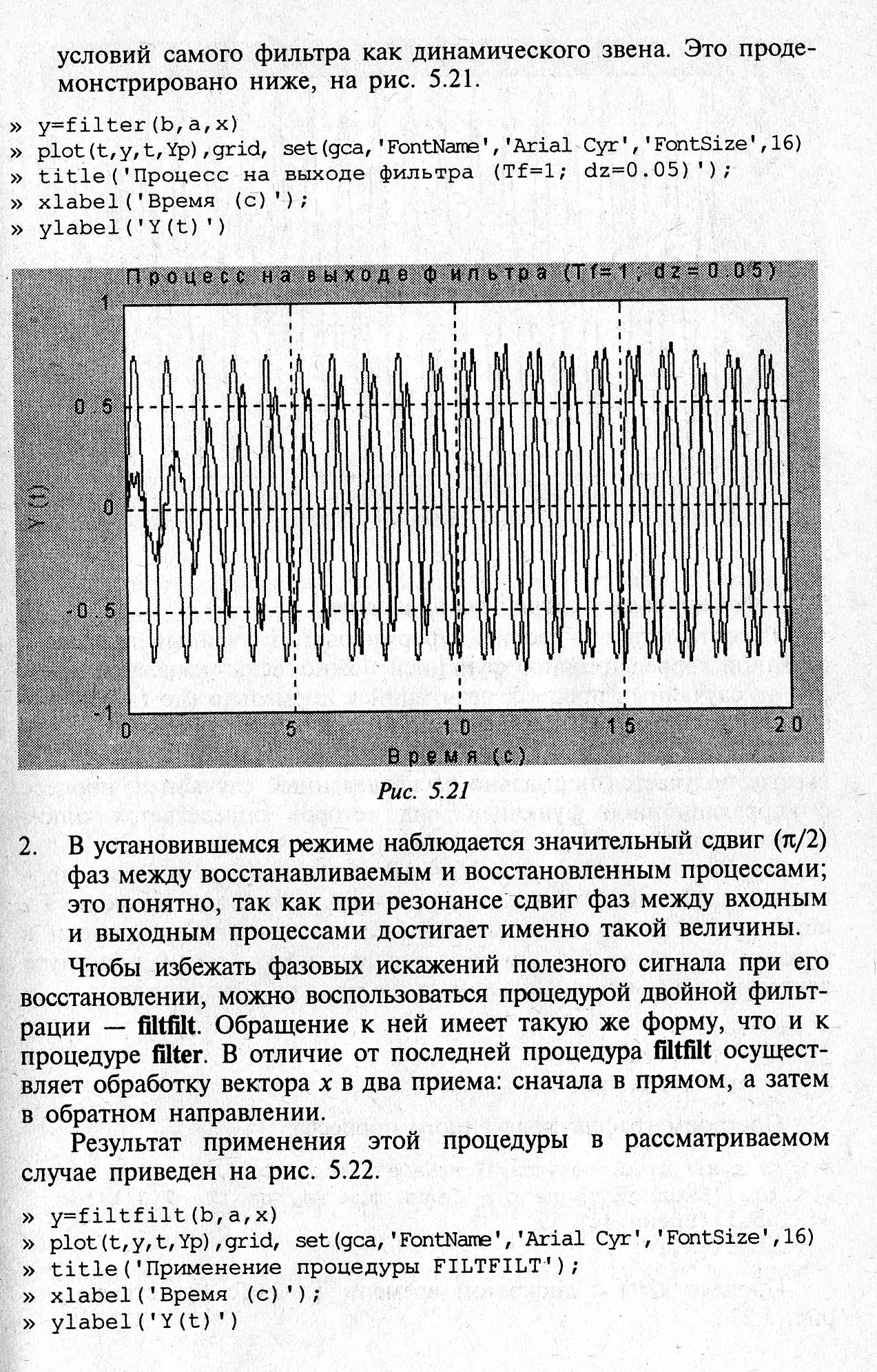
рис 5.

2. в установившемся режиме наблюдается значительный сдвиг фаз, между входным и восстанавливаемым процессами, т.к при резонансе сдвиг фаз достигает именно такой величины.

Для исключения фазовых искажений можно воспользоваться процедурой filtfilt. Процедура filtfilt осуществляет обработку входного вектора в два приема: сначала в прямом, а затем в обратном направлении.