2. Передаточная функция и разностное уравнение цифрового фильтра
Реакция цифрового фильтра на входное воздействие х(п) определяется сверткой этого воздействия с импульсной характеристикой фильтра
у(п)=х(п)*h(п). (.6)
(.7)
Из свойств -преобразования следует, что свертке последовательностей х(п) и h(n) соответствует произведение их -преобразований.
(.8)
Рассматривая Y(z) и X(z) как выходной и входной эффекты цифрового фильтра, используем (.8) для записи общего выражения его передаточной функции:
H(z) = Y(z)/X(z) (.9)
Таким образом, передаточная функция цифрового фильтра является -преобразованием его импульсной характеристики:
(.10)
Рассмотрим пример расчета цифрового фильтра на
основе
аналогового прототипа в виде однозвенной
Г-образной
-цепи. Дискретную импульсную характеристику
запишем в общем виде с учетом масштабирующего
множителя а:
,
(.11)
Где
-
постоянная времени фильтра,
-
интервал дискретизации.
Найдем передаточную функцию цифрового фильтра, определив -преобразование его дискретной импульсной характеристики (ДИХ):
(.12)
Выражение
для
представлено
в ( .13) как сумма членов
геометрической прогрессии со знаменателем
.
Используя
формулу суммирования, получим
,
(.13)
Где
Стуктура записи передаточной функции цифрового фильтра соответствует передаточной функции линейной аналоговой системы с обратной связью:
,
(.14)
Где
-
коэффициент передачи прямого тракта,
-
коэффициент передачи цепи обратной
связи. На рис. приведены функциональные
схемы соответствующей аналоговой
системы
с обратной связью и цифрового фильтра.
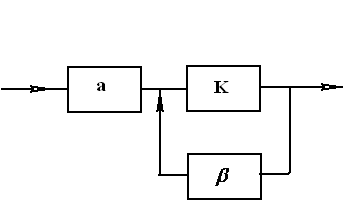
Рис
Из
сопоставления (.13)
и (.14) видно, что
,
а
.
Сопоставление схем позволяет установить
соответствие схемы цифрового фильтра
и системе с обратной связью. Блок,
обозначенный как
выполняет функцию задержки на такт
дискретизации.
Передаточная функция цифрового фильтра, полученная как -преобразование его дискретной импульсной характеристики (ДИХ) в общем виде может быть представлено дробно-рациональным полиномом от переменной .
(.15)
Это
выражение называется уравнением
цифрового фильтра. Коэффициенты
,
называются
коэффициентами цифрового фильтра и их
значения полностью определяют передаточную
функцию фильтра.
Последнее выражение может быть переписано в форме разностного уравнения цифрового фильтра. Из (.15), следует:
(.16)
После выполнения над (.16)обратного -преобразования можно получить:
(.17)
И. в окончательном виде:
(.18)
Коэффициенты разностного фильтра являются соответствующими коэффициентами в уравнении цифрового фильтра.
Z-преобразование
Операторный метод, базирующийся на преобразовании Лапласа, является одним из основных направлений в исследовании линейных систем. Преобразование Лапласа (.1) позволяет осуществить перевод оригинала из области непрерывного времени t в его комплексное изображение E(s) в s-области.
, (.1)
В области дискретного времени преобразование Лапласа последовательности принимает вид суммы:
(.2)
Трансцендентность изображений дискретных .последовательностей из-за наличия экспоненты в ( .2) приводит к определенным трудностям, поэтому применительно к дискретным и цифровым устройствам пользуются не дискретным преобразованием Лапласа, а -преобразованием, которое получается из (:2) заменой :
(.3)
Свойства -преобразования.
Линейность. Если и являются -преобразованиями последовательностей и , то любых действительных а и b z-преобразование равно Это непосредственно вытекает из (.3) и является подтверждением принципа суперпозиции из определения.
Задержка. Если - преобразование относится к последовательности , то -преобразование последовательности ,задержанной на тактов, равно . При определении -преобразования ординаты в соответствии с (.3) умножаются на комплексные числа последовательности и результаты умножения суммируются.
Очевидно, что -преобразование будет точно таким же, если оперировать несмещенной последовательностью и последовательностью смещенной на т тактов в сторону опережения.
Формульная запись при этой операции имеет вид:
(.4)
Из (.4) следует, в частности, что в выражениях z-форм множитель z±m должен рассматриваться как оператор сдвига преобразуемой последовательности на т тактов дискретизации. Знак показателя определяет направление сдвига (минус - задержка, плюс - опережение).
Свертка. Если последовательности соответствует -преобразование , а последовательности -преобразование , то дискретной свертке этих последовательностей:
(.5)
соответствует произведение их - преобразований:
(.6)
Обратное z-преобразование определяется формулой:
(.7)