2.2.3 Расчет удельного количества теплоты q и удельной работы l в процессе 3–4

2.2.3.1 Определение удельного количества теплоты q

Так как процесс 3-4 изохорный, то исходя из определения процесса, имеем:

где с_v – удельная теплоемкость при постоянном удельном объеме, Т₃ и Т₄ – абсолютные температуры газа в точках 3 и 4.

Найденные в пункте 2.2, 2.1.3 и 2.1.4 величины подставляем в выражение , получим:

2.2.3.2 Определение удельной работы l.

Так как процесс 3-4 изохорный, то исходя из определения, процесса имеем:

2.2.4 Расчет удельного количества теплоты q и удельной работы l в процессе 4–1

2.2.4.1 Определение удельного количества теплоты q

Так как процесс 4-1 адиабатный, то исходя из определения процесса, имеем:

2.2.4.2 Определение удельной работы l

Так как процесс 4-1 адиабатный, то исходя из определения работы, имеем:

или

где c_v – удельная теплоемкость при постоянном объеме, Т₁ и Т₄ – абсолютные температуры газа в точках 1 и 4.

Заданные в пункте 1.2 и найденные в пункте 2.1.4 величины подставляем в выражение , получим:

2.3 Расчет изменения удельных величин: внутренней энергии Δu, энтальпии Δh и энтропии Δs в каждом термодинамическом процессе

2.3.1 Определение внутренней энергии Δu, удельной энтальпии Δh, удельной энтропии Δs в процессе 1-2

2.3.1.1 Определение изменения внутренней энергии Δu в процессе 1-2

Так как процесс 1-2 изобарный, то по определению изменения внутренней энергии, находим:

2.3.1.2 Определение изменения удельной энтальпии Δh в процессе 1-2

Так как процесс 1-2 изобарный, то по определению изменения удельной энтальпии, находим:

2.3.1.3 Определение изменения удельной энтропии Δs в процессе 1-2

Так как процесс 1-2 изобарный, то изменение энтропии находится из соотношения:

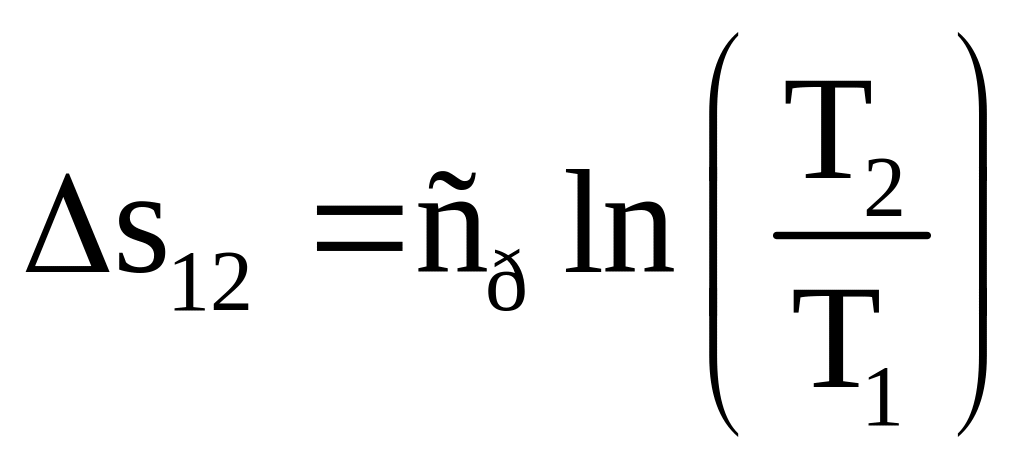
где с_р – удельная теплоемкость при постоянном давлении, Т₁ и Т₂ – абсолютные температуры газа в точках 1 и 2.

Значения, найденные в пунктах 2.1.1, 2.1.2, 2.2 подставляем в выражение , получаем:

2.3.2 Определение внутренней энергии Δu, удельной энтальпии Δh, удельной энтропии Δs в процессе 2-3

2.3.2.1 Определения внутренней энергии Δu в процессе 2-3

Так как процесс 2-3 изотермный, то

2.3.2.2 Определения удельной энтальпии Δh в процессе 2-3

Так как процесс 2-3 изотермный, то

2.3.2.3 Определения удельной энтропии Δs в процессе2-3

Так как процесс 2-3 изотермный, то изменение энтропии находится:

Величины, найденные в пунктах 2.1.2, 2.1.3 и 2.2 подставляем в уравнение, получим:

2.3.3 Определение внутренней энергии Δu, удельной энтальпии Δh, удельной энтропии Δs в процессе 3-4

2.3.3.1 Определение изменения внутренней энергии Δu в процессе 3-4

Так как процесс 3-4 изохорный, то по определению изменения внутренней энергии, находим:

2.3.3.2 Определение изменения удельной энтальпии Δh в процессе 3-4

Так как процесс 3-4 изохорный, то по определению изменения удельной энтальпии, находим:

2.3.3.3 Определение изменения удельной энтропии Δs в процессе 3-4

Так как процесс 3-4 изохорный, то изменение энтропии находится из соотношения :

2.3.4 Определение внутренней энергии Δu, удельной энтальпии Δh, удельной энтропии Δs в процессе 4-1

2.3.4.1 Определения внутренней энергии Δu в процессе 4-1

Так как процесс 4-1 адиабатный, то по определению изменения внутренней энергии, находим:

2.3.4.2 Определения удельной энтальпии Δh в процессе 4-1

Так как процесс 4-1 адиабатный, то по определению изменения удельной энтальпии, находим:

2.3.4.3 Определения удельной энтропии Δs в процессе 4-1

Так как процесс 4-1 адиабатный, то изменение энтропии:

2.3.5 Проверка найденных изменений внутренней энергии Δu, удельной энтальпии Δh, удельной энтропии Δs.

Так как исследуемые термодинамические процессы обратимые, то суммы изменений удельных функций процесса, таких как внутренняя энергия, энтальпия и энтропия, равны нулю.

Найденные в пунктах 2.3.1, 2.3.2, 2.3.3, 2.3.4 значения подставим в выражения , , , получим:

2.4 Расчет величины удельной теплоемкости с и величины показателя политропы n в каждом термодинамическом процессе

2.4.1 Расчет удельной теплоемкости с и величины показателя политропы в процессе 1-2

Так как процесс 1-2 изобарный, выражая с и подставляя ранее найденные величины в выражение , получим:

Величину показателя политропы n найдем из соотношения:

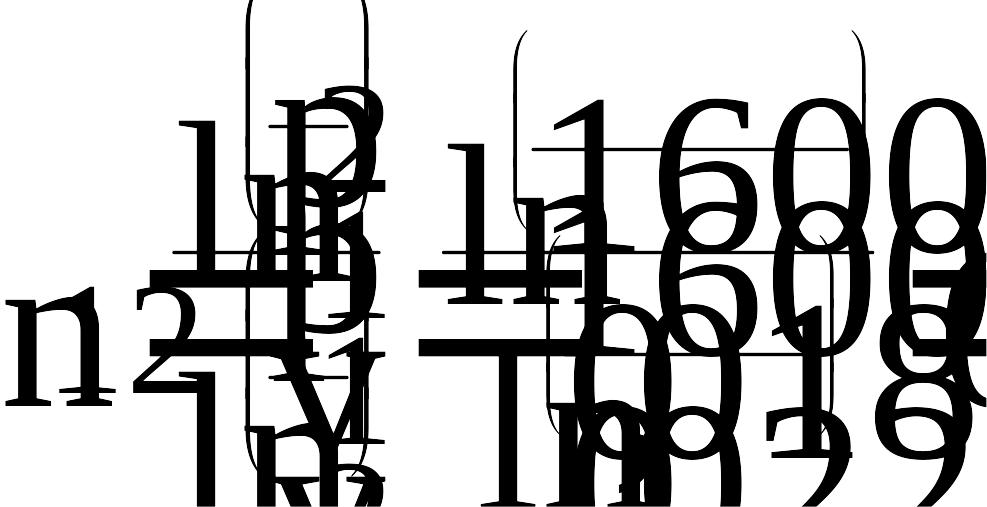
2.4.2 Расчет удельной теплоемкости с и величины показателя политропы в процессе 2-3

Так как процесс 2-3 изотермный, то выражая из уравнения удельную теплоемкость политропного процесса, получим:

где q₂₃ – удельное количество теплоты в процессе 2-3, Т₂ и Т₃ – абсолютные температуры газа в точках 2 и 3.

Величины, найденные ранее, подставляем в уравнение , получаем:

Величину показателя политропы n найдем из соотношения:

где р₂ и р₃ – абсолютные давления газа в точках 2 и 3, v₂ и v₃ – удельные объемы газа в точках 2 и 3.

Полученные ранее значения подставляем в уравнение, имеем:

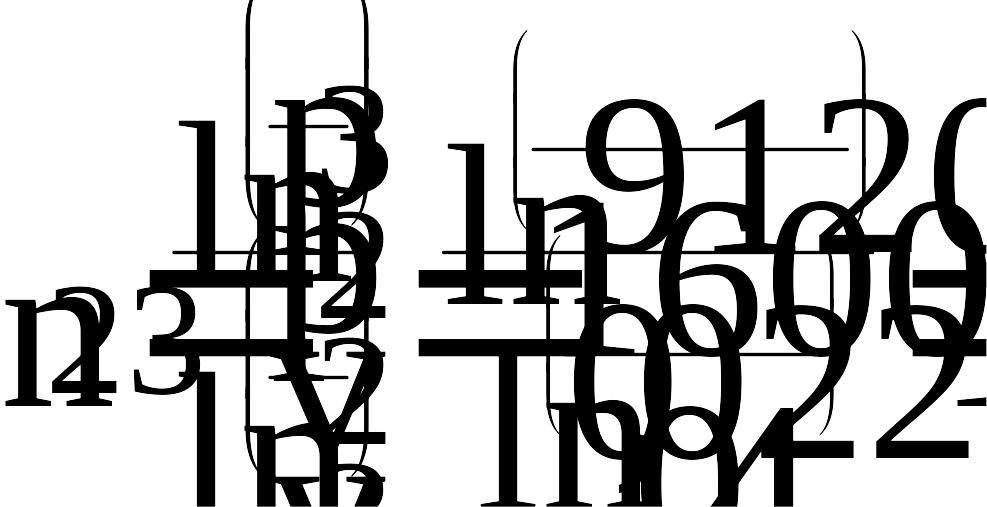
2.4.3 Расчет удельной теплоемкости с и величины показателя политропы в процессе 3-4

Так как процесс 3-4 изохорный, выражая удельную теплоемкость с₃₄ и подставляя ранее найденные величины в выражения , получим:

Величину показателя политропы n найдем из соотношения , подставляя найденные ранее значения:

2.4.4 Расчет удельной теплоемкости с и величины показателя политропы в процессе 4-1

Величины, найденные ранее, подставляем в уравнение, получаем:

Величину показателя политропы n найдем из соотношения , подставляя найденные ранее значения:

2.5 Расчет количества подведенной теплоты q₁ и отведенной теплоты q₂ в цикле, теплоты за цикл q_c, величины работы цикла l_c

2.5.1 Расчет количества подведенной теплоты q₁ в цикле

Подведенная теплота за цикл определяется как алгебраическая сумма всех положительных удельных количеств теплоты за каждый из термодинамических процессов, следовательно:

Для исследуемого цикла, имеем:

2.5.2 Расчет количества отведенной теплоты q₂ в цикле

Отведенная теплота за цикл определяется как модуль алгебраической суммы всех отрицательных удельных количеств теплоты за каждый из термодинамических процессов, следовательно:

Для исследуемого цикла, имеем:

2.5.3 Вывод об исследуемом цикле

Из найденных в пунктах 2.5.1 и 2.5.2 подведенная и отведенная теплоты, можно сделать вывод, что исследуемый нами цикл – прямой цикл , следовательно, исследование ведется для некоторой тепловой машины.

2.5.4 Расчет количества теплоты за цикл q_с

Количество теплоты за цикл определяется, как алгебраическая сумма всех удельных теплот в каждом термодинамическом процессе.

Найденные значения в пункте 2.2 удельных теплот подставляем в выражение , получаем:

2.5.5 Расчет величины работы за цикл l_с

Количество теплоты за цикл определяется, как алгебраическая сумма всех удельных работ в каждом термодинамическом процессе.

Найденные в пункте 2.2 удельные работы подставляем в выражение , получаем:

2.6 Расчет термического КПД η_с цикла

Степень совершенства цикла, в частности превращения в нем теплоты в работу, выражается отношением теплоты , превращенной в работу, к полной теплоте q₁ сообщаемой рабочему телу. Следовательно:

Значения, найденные в пункте 2.5, подставляем , получим:

2.7 Расчет значений удельной энтропии s во всех характерных точках цикла

2.7.1 Расчет удельной энтропии s в точке 1

где T₁ – абсолютная температура газа в точке 1, Т₀ – абсолютная температура газа принятая в пункте 1.2, р₁ – абсолютное давление газа в точке 1, р₀ – абсолютное давление газа принятое в пункте 1.2, с_р – удельная теплоемкость при постоянном давлении, R – удельная газовая постоянная.

Подставляя значения, получим:

2.7.2 Расчет удельной энтропии s в точке 2

Подставляя значения в выражение , получим:

2.7.3 Расчет удельной энтропии s в точке 3

Подставляя значения в выражение , получим:

2.7.4 Расчет удельной энтропии s в точке 4

Подставляя значения в выражение , получим:

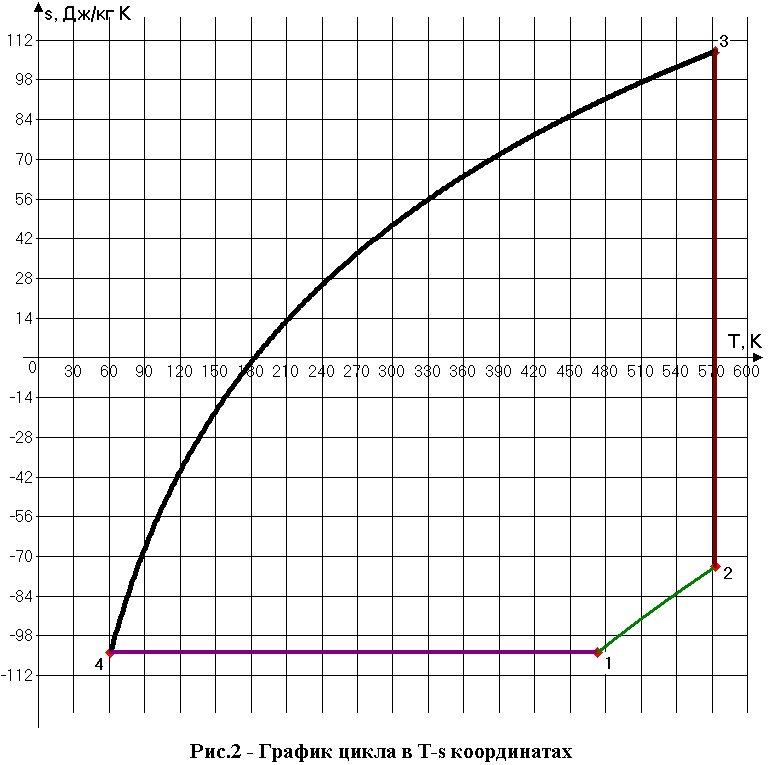
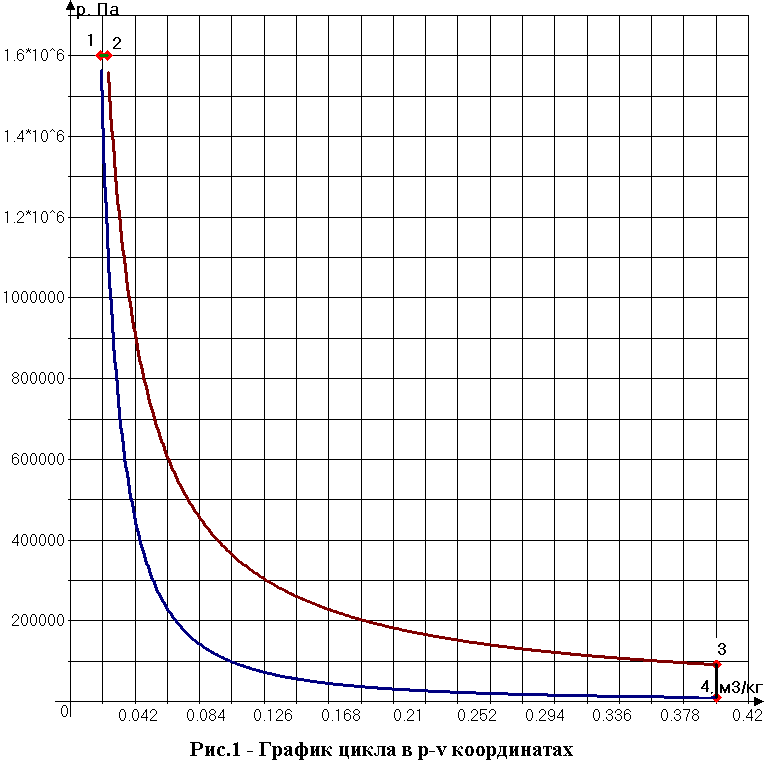
2.8 Графики цикла в p-v и T-s координатах

Графики выполнены с использованием программы Advanced Grapher 2.11.

Уравнение для процесса 1-2 , где . Уравнение для процесса 2-3 на отрезке .

Уравнение для процесса 3-4 на отрезке .

Уравнение для процесса 4-1 , где .

Уравнение для процесса 1-2 выглядит:

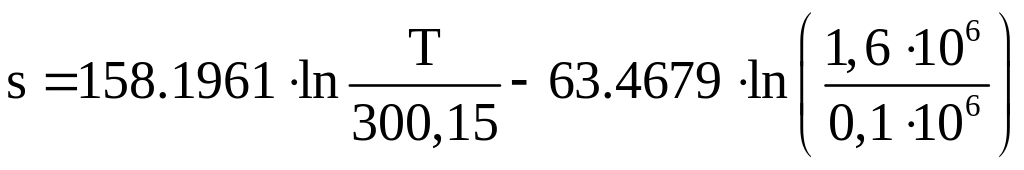на отрезке .

Уравнение для процесса 2-3 выглядит:

на отрезке

Уравнение для процесса 3-4:

на отрезке .

Уравнение для процесса 4-1:

на отрезке