
- •6.100102 – «Процессы, машины и оборудование агропромышленного
- •Содержание
- •1. Типы плоских кулачковых механизмов
- •2. Задачи проектирования (синтеза) кулачкового механизма
- •3. Исходные данные
- •4. Построение кинематических диаграмм (графиков)
- •4.1. Синусоидальный закон
- •4.2. Косинусоидальный закон
- •4.3. Параболический закон
- •4.4. Линейный закон
- •5. Определение минимального радиуса кулачка
- •5.2. Определение минимального радиуса для кулачкового механизма с игольчатым или роликовым толкателем
- •6. Построение профиля кулачка
- •6.1. Построение профиля кулачка для кулачкового механизма с центральным роликовым толкателем
- •6.2. Построение профиля кулачка для кулачкового механизма с центральным игольчатым толкателем
- •6.3 Построение профиля кулачка с центральным тарельчатым (плоским) толкателем
- •6.4 Построение профиля кулачка для механизма с эксцентрично поставленным роликовым толкателем
- •6.5 Построение профиля кулачка для механизма с эксцентрично поставленным игольчатым толкателем
- •6.6 Построение профиля кулачка для механизма с эксцентрично поставленным тарельчатым толкателем
- •Литература
6.3 Построение профиля кулачка с центральным тарельчатым (плоским) толкателем
Закон движения толкателя задан в виде диаграммы S=f(φ), изображенных на рисунках 2, 3, 4 и 5, на которых показаны все фазы движения толкателя за один оборот кулачка. Из произвольно выбранной точки О (рис. 9) проводим окружность радиусом , определенным по методу, описанному выше.
Для построения профиля кулачка сообщают кулачку угловую скорость ω. От прямой ОА противоположно направлению ω, откладывают фазовые углы φ1, φ2, φ3 и φ4. Дуги, стягивающие фазовые углы φ1 и φ3, делят на столько же частей, на сколько разделена ось абсцисс диаграмм S=f(φ1) и S=f(φ3) (в нашем случае на 8). Через точки 0, 1, 2, 3, ... , 17 проводят лучи из центра О. Если масштаб чертежа равен масштабу диаграммы перемещений (т.е. = ), то на лучах от точек 0, 1, 2, …, 17 откладывают отрезки, равные ординатам диаграммы S=f(φ) и соответствующие углам поворота кулачка, получают точки 0*, 1*, 2*, …, 17*. Соединив эти точки плавной кривой, получим теоретический профиль кулачка на фазах подъема и опускания.
На фазе верхнего стояния профиль кулачка будет дугой окружности , на фазе нижнего стояния - дугой Для построения практического профиля через точки 0*, 1*, 2*... 17* проводим перпендикуляры к лучам О-0*, О-1*, О-2*, ... О-17*. Практическим профилем кулачка будет внутренняя огибающая этих перпендикуляров.
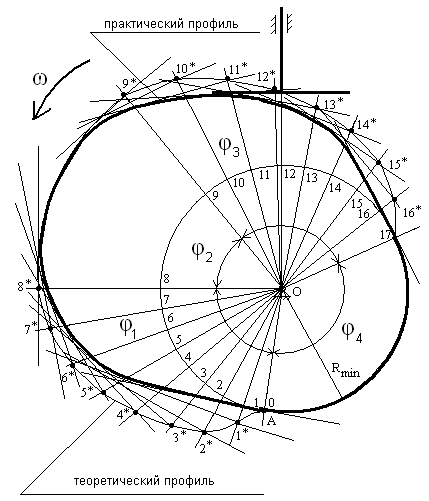
Рис. 10 Построение профиля центрального тарельчатого кулачкового механизма
6.4 Построение профиля кулачка для механизма с эксцентрично поставленным роликовым толкателем
При построении
профиля кулачка данного вида из центра
вращения кулачка О проводят
окружность: радиусом равным смещению
е. Если чертеж выполняется при условии
равенства масштабов
![]() =
,
то радиус этой окружности равен
(см. рис. 11).
=
,
то радиус этой окружности равен
(см. рис. 11).
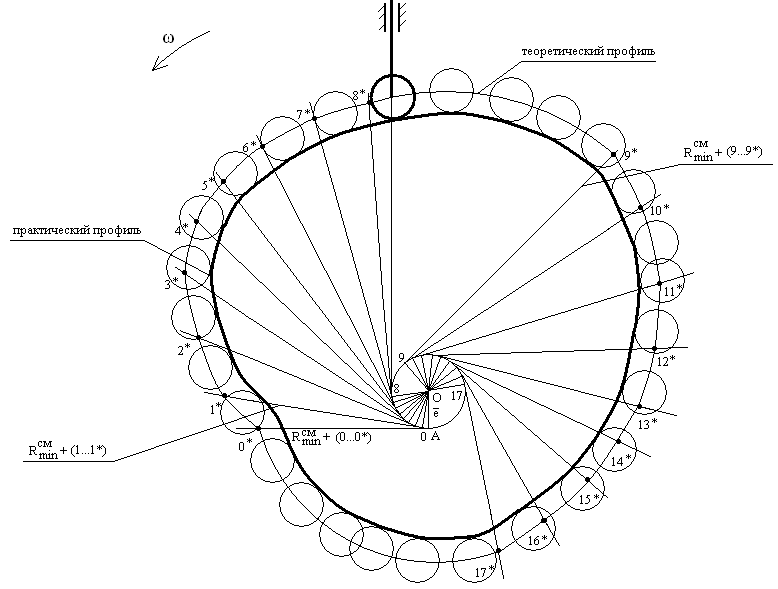
Рис. 11 Построение профиля роликового кулачкового механизма со смещением
Для построения
профиля кулачка сообщают кулачку угловую
скорость ω.
От прямой ОА противоположно направлению
ω
откладывают фазовые углы φ1,
φ2,
φ3
и φ4.
Дуги, стягивающие фазовые углы φ1
и φ3,
делят на столько же частей, на сколько
разделена ось абсцисс диаграмм S=f(φ1)
и S=f(φ3)
(в нашем
случае на 8). Через точки 0, 1,
2, 3, ... , 17 проводят
касательные к окружности с радиусом
в сторону, противоположную угловой
скорости кулачка. Если масштаб чертежа
равен масштабу диаграммы перемещений
(т.е.
=
),
то на касательных от точек 0, 1, 2, …, 17
откладывают отрезки, равные сумме
минимального радиуса кулачка со смещением
(см. пункт 5.1 и 5.2) и соответствующей
ординаты диаграммы S=f(φ).
Например, на касательной, проведенной
к радиусу О-0, отложим отрезок
![]() ,
на касательной
к радиусу О-1 – отрезок
,
на касательной
к радиусу О-1 – отрезок
![]() и т.д. При
этом получают точки 0*, 1*, 2*, …, 17*. Соединив
эти точки плавной кривой, получим
теоретический профиль кулачка на фазах
подъема и опускания.
и т.д. При
этом получают точки 0*, 1*, 2*, …, 17*. Соединив
эти точки плавной кривой, получим
теоретический профиль кулачка на фазах
подъема и опускания.
На фазах дальнего и ближнего стояния профиль кулачка будет дугой окружности. Если толкатель роликовый, то построение практического профиля сводится к построению эквидистантной кривой как огибающей положений ролика (см. рис. 11).
Радиус ролика принимают по формуле (16).
