Геометрия: с нуля до группы с
Вот задача пробного ЕГЭ по математике 2010 года (часть В).
Коробка имеет форму куба, длина ребра которого 5 сантиметров. Какое максимальное количество кубиков с длиной ребра 2 сантиметра можно в ней разместить?
Ни один из отличников, пришедших заниматься в мои группы подготовки к ЕГЭ по математике, не решил эту задачу с первого раза. Им, оказывается, сложно представить, а тем более — нарисовать, как кубики сложены в коробку. Самое распространённое решение, которое я видела — объём коробки делили на объём кубика и записывали в ответ!
И поэтому на занятиях в мини-группах и на интенсиве освоение курса геометрии приходилось начинать с нуля.
Начиналось всё с подготовительной работы. Каждый из учеников получал список основных понятий, теорем, формул, свойств геометрических фигур, которые необходимо было выучить, а также список простых задач. Например, построить три высоты в тупоугольном треугольнике или доказать, что сумма углов треугольника равна 180 градусов.
Некоторые вопросы ставят абитуриентов в тупик. Например, «признаки равенства треугольников» в учебнике находят все, а слова «неравенство треугольника» считают опечаткой.
Лишь после этого появлялась возможность перейти к решению простых задач, а затем — к экзаменационным задачам, которые в пробных вариантах ЕГЭ обычно имеют номер С4.
Одна из особенностей ЕГЭ по математике 2010 года (судя по пробным и тренировочным вариантам) — условие задачи предполагает не один, а два (иногда три) возможных чертежа и, соответственно, два или три решения, два или три правильных ответа. Все эти случаи надо заметить и рассмотреть.
Я всегда говорю абитуриентам, что у школьной программы по математике нет чётких границ. Например, теорема о биссектрисе треугольника присутствует в учебнике Л. С. Атанасяна, но только в виде задачи. Разобрали задачу на уроке — значит, повезло. Теорема о секущей и касательной — та же история.
И когда мои абитуриенты уже самостоятельно решают задачи ЕГЭ по математике уровня С4, я устраиваю спектакль.
У меня есть два коронных номера. Я предупреждаю слушателей, что сейчас буду их бессовестно обманывать, а их задача — разоблачить обман. У них загораются глаза. Они готовы ловить каждое моё слово, лишь бы только уличить хитрого преподавателя.
Читайте дальше — Геометрические парадоксы.
Геометрический парадокс: катет равен гипотенузе!
Сейчас я вам докажу, что катет равен гипотенузе.
И рисую новый чертёж, с новым «доказательством».
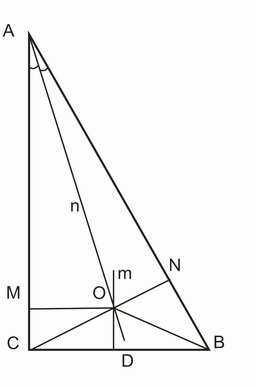
Построим прямоугольный треугольник АВС, угол С равен 90 градусов. Пусть точка D — середина ВС. Проведем лучи n — биссектрису угла А, и m — серединный перпендикуляр к ВС. Лучи n и m пересекаются в точке О.
Опустим из точки О перпендикуляры на стороны АВ и АС. Точки М и N — основания этих перпендикуляров. Рассмотрим треугольники АМО и АNО. Они равны, так как оба они — прямоугольные, угол МАО равен углу NAO (по построению), гипотенуза АО —общая. Следовательно, ОМ = ON, AM = AN.
Рассмотрим треугольники СОD и OBD. Они равны, так как ОD — серединный перпендикуляр к ВС (по построению), то есть медиана и высота треугольника СОВ. Следовательно, ОС = ОВ.
Рассмотрим треугольники МСО и NBO. Они оба — прямоугольные, ОС = ОВ, ОМ = ON (по доказанному), следовательно, треугольник МСО равен треугольнику NBO, и поэтому МС = NB.
Ну а дальше всё просто :-) Как мы уже доказали, МС = NB, AM = AN. Следовательно, МС + AM = NB + AN, АС = АВ, катет равен гипотенузе, что и требовалось доказать :-)
Всё повторяется — но на этот раз ребятам всё-таки уже проще отстаивать собственное мнение, проще строить настоящее доказательство, основанное не на эмоциях, а на знаниях.
Может быть, в этом и ответ на вопрос: «Зачем учить геометрию». Не только для того, чтобы не просчитаться с покупкой рулонов обоев! Кроме практической пользы, в геометрии есть особый смысл. Логическое мышление — один из путей к независимости личности.
Научной и нравственной основой курса геометрии является принцип доказательности всех утверждений. И это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на последовательном выводе всех утверждений. Людьми, понимающими, что такое доказательство, трудно и даже невозможно манипулировать.
Из статьи И.Ф.Шарыгина «Нужна ли школе 21-го века Геометрия»
Впрочем, если вы всё ещё считаете, что геометрия вам не нужна — это ваш выбор. Вам будут продавать столько рулонов обоев (и всего остального), сколько посчитают нужным :-)