Контрольные вопросы

1. Что называется звуком? На какие виды делятся звуки?

2. Чем сложный тон отличается от простого? Нарисуйте акустический спектр простого и сложного тона.

3. Что представляет собой шум? звуковой удар?

4. Укажите физические характеристики звука.

5. Перечислите субъективные характеристики звука и укажите, как они связаны с объективными характеристиками.

6. Что называется громкостью? В каких единицах измеряется громкость?

7. Сформулируйте закон Вебера – Фехнера, запишите формулу для определения громкости звука.

8. Что называется кривыми равной громкости?

9. В каком диапазоне частот наиболее чувствительно среднее человеческое ухо?

10. Что называется аудиометрией? аудиограммой?

11. Расскажите о строении и назовите основные функции наружного, среднего и внутреннего уха.

12. Объясните функциональное назначение элементов внутреннего уха.

13. Объясните последовательность формирования слухового ощущения.

Использованная и рекомендуемая литература

1. Блохина М.Е., Эссаулова И.А., Мансурова Г.В. Руководство к лабораторным работам по медицинской и биологической физике. М.: Дрофа, 2001. - 288 с. (Раздел 2. стр.52-57)

2. Джерри Мерион Б. Общая физика с биологическими примерами. М.: Высш. шк., 1986. 623 с. (§ 14.3 стр.366-382)

3. Владимиров Ю.А., Рощупкин Д.И., Потапенко А.Я., Деев А.И. Биофизика. М.: Медицина, 1983. (§ 13.2 стр.252-258)

4. Ремизов А.Н., Максина А.Г., Потапенко А.Я. Медицинская и биологическая физика. М.: Дрофа, 2003.- 558 с. (Глава 6. § 6.1 - § 6.5 стр.93-107)

Дополнительная литература

1. Джанколи Д. Физика. М.: Мир, Т.1. 1989. - 653 с. (Том 1. Глава 16 § 16.1 стр.465-467; § 16.5 стр.477-478; § 16.8 стр.485-487)

2. Губанов, Н.И. Медицинская биофизика / Н.И. Губанов, А.А. Утепенбергов. – М.: Медицина, 1978. – 304 с. (Глава 13. стр.296-304)

3. Руководство к лабораторным работам по медицинской и биологической физике/ Под ред. Кудрявцева В.А. - Киров: КГМА, 1999.-278с. (часть II стр.51-56)

Глава 3 «строение и свойства жидкостей» лабораторная работа № 5 определение вязкости жидкости методом стокса

Цель работы: экспериментальное определение коэффициента внутреннего трения в жидкости по методу Стокса.

Задачи работы: 1) определение коэффициента вязкости глицерина; 2) определение числа Рейнольдса и характера обтекания шарика жидкостью.

Обеспечивающие средства: микрометр, секундомер, линейка, стеклянный цилиндрический сосуд с жидкостью, свинцовые шарики.

Теоретическая часть

Вязкость (внутреннее трение) – свойство текучих тел (жидкостей или газов) оказывать сопротивление перемещению одной их части относительно другой.

Вязкость в жидкостях и газах обусловливается переносом импульса молекул поперек направления движения слоев газа, имеющих различные скорости. В результате теплового движения молекулы перелетают из одного слоя газа в другой, перенося при этом свой импульс упорядоченного движения из одного слоя в другой. Вследствие обмена молекулами импульс упорядоченного движения быстрее движущегося слоя уменьшается, а слой тормозится, импульс медленнее движущегося слоя увеличивается, и слой ускоряется. В этом и состоит механизм возникновения силы внутреннего трения (вязкости) между слоями жидкости или газа, движущимися с различными скоростями.

Жидкость без вязкости (так называемая идеальная жидкость) является абстракцией. Всем реальным жидкостям присуща вязкость.

Режимы течения жидкости разделяются на ламинарное и турбулентное. Ламинарным (слоистым) называется упорядоченное течение жидкости, при котором смежные слои как бы скользят друг относительно друга. Для ламинарного течения характерны гладкие квазипараллельные траектории частиц жидкости.

Чтобы непосредственно наблюдать за характером движения частиц, необходимо сделать видимым движение потока воды или воздуха. В воздухе это легко осуществить при помощи дыма. В воде удобно применить подкрашивание струек какой-нибудь жидкой краской или чернилами. Если пропускать, например, поток воды по стеклянной трубке и ввести в трубку тонкую трубочку, через которую подавать струйку чернил, то в ламинарном потоке чернильная струйка вытянется вдоль стеклянной трубки (рис.1).

С увеличением скорости движения ламинарное течение становится турбулентным. Турбулентное течение характеризуется наличием многочисленных вихрей, что приводит к перемешиванию между слоями жидкости. В описанном выше опыте расплывание чернильной струйки укажет на турбулентность потока воды.

Рис.1

Возникновение турбулентности часто бывает внезапным и определяется числом Рейнольдса Re. Для течения жидкости в круглой трубе

(1)

где  и  - плотность и вязкость жидкости, v – средняя по поперечному сечению трубы скорость течения, R – радиус трубы, D - диаметр трубы.

Когда значение Re меньше критического Re_кр  2300, течение жидкости является ламинарным, если Re > Re_кр, то течение становится турбулентным. Как правило, движение крови по сосудам является ламинарным. Однако в ряде случаев возможно возникновение турбулентности. Турбулентное движение крови в аорте может быть вызвано прежде всего турбулентностью кровотока у входа в нее: вихри потока уже изначально существуют, когда кровь выталкивается из желудочка в аорту, что хорошо наблюдается при доплер-кардиографии. У мест разветвления сосудов, а также при возрастании скорости кровотока (например, при мышечной работе) течение может стать турбулентным и в артериях. Турбулентное течение может возникнуть в сосуде в области его локального сужения, например, при образовании тромба.

Турбулентное течение связано с дополнительной затратой энергии при движении жидкости, поэтому в кровеносной системе это может привести к дополнительной нагрузке на сердце. Шум, возникающий при турбулентном течении крови, может быть использован для диагностики заболеваний. При поражении клапанов сердца возникают так называемые сердечные шумы, вызванные турбулентным движением крови.

Когда тело движется относительно жидкости (газа), на него действует сила со стороны среды. Эта сила называется силой лобового сопротивления (силой вязкого трения); она возникает благодаря вязкости среды, а также (при больших скоростях) вследствие возникновения турбулентности позади тела.

Для описания движения тела сферической формы относительно жидкости или газа удобно ввести еще одно число Рейнольдса

(2)

где  и  - плотность и вязкость жидкости, – скорость тела относительно среды, r – радиус тела. Следует четко отличать это число Рейнольдса Re от числа Рейнольдса Re для течения жидкости (газа) в трубе; они хотя и похожи по виду, но относятся к разным явлениям.

Обтекающий тело поток является ламинарным, если Re  1; при больших значениях числа Рейнольдса (обычно в интервале 1 – 10) в потоке позади тела возникает турбулентное течение.

Сила вязкого трения, действующая на малое сферическое тело в ламинарном потоке, определяется формулой Стокса

(3)

где  - коэффициент вязкости жидкости (динамическая вязкость), r - радиус шарика, - скорость шарика. Знак « - » в формуле (3) означает, что сила трения и вектор скорости движения тела направлены противоположно друг другу.

В системе СГС вязкость измеряется в пуазах (1Пз = г/(см с)), в системе СИ [ = кг/(м с).

Под осаждением (седиментацией) понимают падение малых тел в жидкой или газообразной среде.

На шарик, падающий в жидкости (рис.2), действует сила тяжести , направленная вниз, и направленные вверх сила трения и сила Архимеда .

Рис.2

Cила тяжести и сила Архимеда, соответственно, равны:

(4)

и

, (5)

где g – ускорение свободного падения; m, V – масса и объем шарика; и - плотности шарика и жидкости, соответственно.

Найдем уравнение движения шарика. По второму закону Ньютона:

(6)

Для проекций на вертикальную ось, с учетом (3-5), получим:

. (7)

Данное уравнение можно привести к виду:

. (8)

Решение этого уравнения имеет вид:

, (9)

где – установившаяся скорость, определяемая уравнением

(10)

а  - время релаксации, примерно равное промежутку времени, в течение которого скорость тела достигает значения установившейся скорости . (Рассчитаем точное значение скорости v(t) в момент времени, равный времени релаксации . Если в формуле (9) взять t =  , тогда v(t) = v₀ · (1 – e^-1) ≈ 0,63 · v₀ .) Время релаксации определяется соотношением

(11)

Как видно из (9), скорость шарика экспоненциально приближается к установившейся скорости (рис.3).

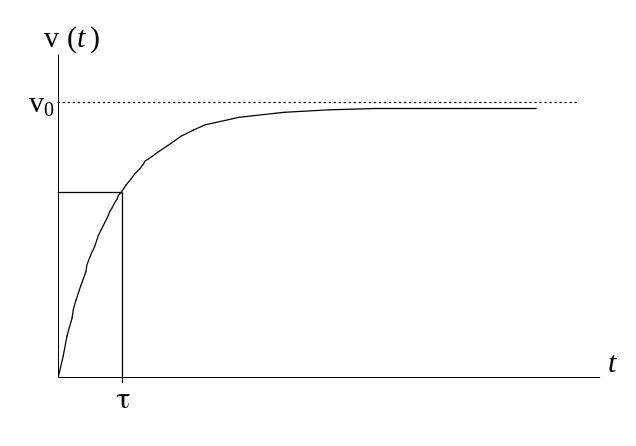
Рис.3

Если время падения в несколько раз больше времени релаксации, можно считать, что падение происходило с постоянной скоростью, и для определения коэффициента вязкости можно воспользоваться формулой (10), из которой следует:

. (12)

Скорость равномерного движения определяется по формуле

, (13)

где t - время движения шарика на пути L. Подставив (13) в уравнение (12), получим формулу для определения коэффициента вязкости методом Стокса

. (14)