
- •Глава I. Векторная алгебра.
- •§1. Векторы в пространстве. Основные определения.
- •§2. Линейные операции над векторами.
- •I. Сложение векторов.
- •I I. Умножение вектора на число.
- •§3. Проекция вектора на ось.
- •§4. Линейно зависимые и линейно независимые системы векторов.
- •§5. Базис. Координаты. Размерность.
- •§6. Скалярное произведение.
- •§7. Скалярное произведение в координатной форме.
- •§8. Направляющие косинусы вектора.
- •§9. Ориентация базиса в пространстве.
- •§10. Векторное произведение.
- •§11. Смешанное произведение трех векторов.
- •Глава II. Аналитическая геометрия на плоскости и в пространстве.
- •§1. Декартова система координат.
- •§2. Простейшие задачи аналитической геометрии.
- •§2. Аналитическая геометрия на плоскости.
- •§3. Прямая на плоскости.
- •§4. Специальные виды уравнения прямой.
- •§5. Основные задачи, связанные с прямой.
- •§6. Алгебраические линии на плоскости.
- •§7. Окружность.
- •§8. Эллипс.
- •§9. Гипербола.
- •§10. Парабола.
- •§11. Кривые второго порядка – заключение.
- •§12. Аналитическая геометрия в пространстве.
- •§13. Плоскость в пространстве.
- •§14. Специальные случаи уравнения плоскости.
- •§15. Основные задачи, связанные с плоскостью.
- •§16. Прямая в пространстве.
- •§17. Основные задачи.
- •§18. Поверхности в пространстве.
- •§19. Поверхность вращения.
- •§20. Проекция линии пересечения двух поверхностей на координатную плоскость.
- •§21. Поверхности второго порядка. Исследование методом сечений.
- •§22. Эллипсоид.
- •§23. Гиперболоиды и конус.
- •§24. Параболоиды.
§2. Аналитическая геометрия на плоскости.
В этом и нескольких последующих параграфах будут рассмотрены основные задачи аналитической геометрии на плоскости.
Пусть дана некоторая фиксированная координатная плоскость, т.е. плоскость, на которой
задана декартова система координат XOY и ортонормированный базис {i, j}, орты которого сонаправлены координатным осям х и у соответственно.
Любая точка плоскости определяется двумя координатами – координатами своих ортогональных проекций на эти оси: М(х, у).
Любой вектор плоскости так же определяется двумя координатами – коэффициентами разложения по базису или, что то же самое, своими проекциями на координатные оси: а = (ах , ау).
Линия на плоскости определяется как геометрическое место точек плоскости (гмт), удовлетворяющих некоторому геометрическому или аналитическому условию. Геометрическое условие необходимо перевести в аналитическое (геометрия – аналитическая!), а у аналитического
− выяснить геометрический смысл (аналитическая геометрия). Аналитическим заданием линии является уравнение с двумя переменными: F(x, y) = 0, т.е. линия на плоскости определяется как
геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Иногда линия
задается в параметрической форме:
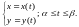
Замечание. В математическом анализе уравнение F(x, y) = 0 называют неявным заданием функции
(частный случай y = f (x) называется явным заданием), т.е. используются понятия функции и аргумента. В аналитической геометрии, вообще говоря, переменные х и у считают равноправными.
§3. Прямая на плоскости.
Определим прямую l на плоскости следующим образом:
Пусть заданы
произвольная фиксированная т. М0(х0,у0) и произвольный фиксированный
и произвольный фиксированный
ненулевой
вектор
 ,
перпендикулярный данной прямой, который
называется
,
перпендикулярный данной прямой, который
называется
нормальным вектором прямой или просто нормалью.
Прямой,
проходящей через т. М0 , с данным
нормальным вектором
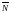 называется геометрическое место концов
векторов на плоскости, имеющих начало
в т. М0 и ортогональных вектору
(рис.3).
называется геометрическое место концов
векторов на плоскости, имеющих начало
в т. М0 и ортогональных вектору
(рис.3).
Используя данное определение, легко написать аналитическое задание или уравнение этой прямой.
 у Пусть т.
М(х,у) − произвольная точка
прямой.
у Пусть т.
М(х,у) − произвольная точка
прямой.
Из условия сразу следует:
М0
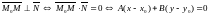
М х Итак,
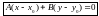 − уравнение прямой, проходящей
− уравнение прямой, проходящей
Рис.3 через точку
(х0,у0) и перпендикулярной
вектору
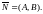
Если обозначить выражение − Ах0 − Ву0 через С , то получим
общее уравнение прямой
на плоскости:
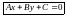
§4. Специальные виды уравнения прямой.
Уравнение с угловым коэффициентом.
Хорошо известное уравнение y = k x + b, где k = tgφ − тангенс угла наклона прямой к оси ОХ ,
а b − величина отрезка от начала координат до точки пересечения прямой с осью OY .
II. Уравнение прямой, проходящей через две заданные точки.
Так как прямая полностью определяется двумя точками, естественно написать соответствующее уравнение. Пусть даны две различные точки, принадлежащие прямой l:
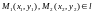 .
В этом случае
.
В этом случае
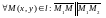 .
Отсюда :
.
Отсюда :
 − уравнение прямой через две точки.
− уравнение прямой через две точки.
III. Каноническое и параметрические уравнения прямой.
Любой вектор, коллинеарный прямой l называется направляющим вектором прямой.
(В частности, вектор
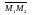 (пункт
II) − направляющий) Если
дана точка на
(пункт
II) − направляющий) Если
дана точка на
прямой и направляющий вектор
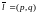 ,
то последнее уравнение можно переписать
в виде:
,
то последнее уравнение можно переписать
в виде:
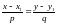 − каноническое уравнения прямой.
Если полученную пропорцию приравнять
− каноническое уравнения прямой.
Если полученную пропорцию приравнять
к параметру t , то
получим параметрические уравнения
прямой:
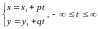 .
.
IV. Уравнение прямой в отрезках.
Пусть известны точки пересечения прямой
с осями координат:
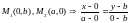 .
.
Отсюда :
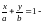 уравнение прямой в отрезках.
уравнение прямой в отрезках.
