§16. Прямая в пространстве.

Наиболее простым заданием прямой в пространстве является ее задание, как линии пересечения двух плоскостей: .

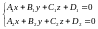(Естественно предполагать, что плоскости не совпадают и не параллельны)

Однако, такое задание имеет большой недостаток: оно не содержит в явном виде ни одной геометрической характеристики прямой. Удобнее пользоваться каноническим уравнением прямой, в котором она определяется как геометрическое место концов векторов, имеющих общее начало и коллинеарных данному ненулевому вектору − направляющему вектору прямой.

Если обозначить любую фиксированную точку прямой через М₀ , а направляющий вектор 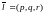, то для произвольной точки прямой М получим соотношение:

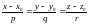− каноническое уравнение прямой в пространстве. (См. §4,п.III)

Замечание. На самом деле, каноническое уравнение представляет собой систему двух линейных уравнений с тремя переменными, т.е. линию пересечения двух плоскостей. Но, во – первых, это

особые плоскости (параллельные координатным осям) и, во – вторых, в записи системы геометрические характеристики прямой фигурируют в явном виде.

Пример. Перейти к каноническому заданию:

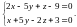
{Положим z = 0. Тогда x =2, y = − 1; 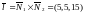. Отсюда: }

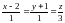От канонического уравнения легко перейти к параметрическому заданию. Приравняем полученную пропорцию к новой переменной и выразим через нее переменные x, y и z:

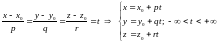
Пример. Найти точку пересечения прямой 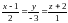с плоскостью x – y +2z – 11 = 0.

{x = 1 + 2t, y = −3t, z = −2 + t → 7t − 14 = 0 → t = 2 → (5, −6, 0) }

Уравнение прямой через две точки можно написать, взяв в качестве направляющего вектора вектор :

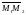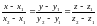
(#) В некоторых задачах удобно пользоваться векторным представлением прямой. В этом случае прямая задается радиус – вектором (§1) текущей точки прямой.

(рис.9)

Здесь :

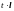M r₀ − радиус – вектор т. М₀

M₀ l = (p, q, r) − направляющий вектор прямой.

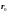
рис.9

§17. Основные задачи.

Две задачи, связанные с прямой были уже рассмотрены на примерах в предыдущем параграфе.

Задачи, связанные с вычислением углов между прямыми, прямой и плоскостью, включая условия ортогональности и параллельности, решаются с использованием направляющих векторов прямых и нормальных векторов плоскостей. Так, например, синус угла между прямой и плоскостью будет равен модулю косинусу угла между соответствующими направляющим и нормальным векторами:

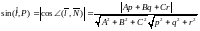
Условия ортогональности и параллельности прямой и плоскости записываются следующим образом:

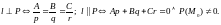
Рассмотрим две прямые с направляющими векторами 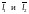и проходящие через точки М₁ и М₂ соответственно. Прямые могут пересекаться, быть параллельными или скрещиваться. В двух первых случаях смешанное произведение 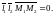Если же прямые скрещиваются, то

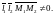Оба условия являются необходимыми и достаточными. Так как расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат, то оно может быть найдено по формуле 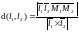− объем параллелепипеда

деленный на площадь основания.

Пример. Как расположены прямые 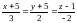и ?

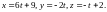Если они пересекаются – найти общую точку. Если нет – расстояние между ними.

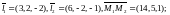
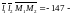{ прямые скрещиваются.

}
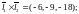
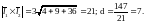