
- •Глава I. Векторная алгебра.
- •§1. Векторы в пространстве. Основные определения.
- •§2. Линейные операции над векторами.
- •I. Сложение векторов.
- •I I. Умножение вектора на число.
- •§3. Проекция вектора на ось.
- •§4. Линейно зависимые и линейно независимые системы векторов.
- •§5. Базис. Координаты. Размерность.
- •§6. Скалярное произведение.
- •§7. Скалярное произведение в координатной форме.
- •§8. Направляющие косинусы вектора.
- •§9. Ориентация базиса в пространстве.
- •§10. Векторное произведение.
- •§11. Смешанное произведение трех векторов.
- •Глава II. Аналитическая геометрия на плоскости и в пространстве.
- •§1. Декартова система координат.
- •§2. Простейшие задачи аналитической геометрии.
- •§2. Аналитическая геометрия на плоскости.
- •§3. Прямая на плоскости.
- •§4. Специальные виды уравнения прямой.
- •§5. Основные задачи, связанные с прямой.
- •§6. Алгебраические линии на плоскости.
- •§7. Окружность.
- •§8. Эллипс.
- •§9. Гипербола.
- •§10. Парабола.
- •§11. Кривые второго порядка – заключение.
- •§12. Аналитическая геометрия в пространстве.
- •§13. Плоскость в пространстве.
- •§14. Специальные случаи уравнения плоскости.
- •§15. Основные задачи, связанные с плоскостью.
- •§16. Прямая в пространстве.
- •§17. Основные задачи.
- •§18. Поверхности в пространстве.
- •§19. Поверхность вращения.
- •§20. Проекция линии пересечения двух поверхностей на координатную плоскость.
- •§21. Поверхности второго порядка. Исследование методом сечений.
- •§22. Эллипсоид.
- •§23. Гиперболоиды и конус.
- •§24. Параболоиды.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Глава I. Векторная алгебра.
§1. Векторы в пространстве. Основные определения.
Определение 1. Вектором в пространстве называется направленный отрезок.
Таким
образом, векторы в отличие от скалярных
величин имеют две характеристики: длину
и направление. Будем обозначать векторы
символами
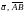 ,
или а.
,
или а.
(Здесь А
и В – начало и конец данного вектора
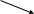 (рис.1)) а
В
(рис.1)) а
В
Длина вектора
обозначается символом модуля:
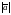 .
А рис.1
.
А рис.1
Различают три вида векторов, задаваемых отношением равенства между ними:
Закрепленные векторы называются равными, если у них совпадают начала и концы соответственно. Примером такого вектора является вектор силы.
Скользящие векторы называются равными, если они расположены на одной прямой, имеют одинаковые длины и направления. Примером таких векторов является вектор скорости.
Свободные или геометрические векторы считаются равными, если они могут быть совмещены с помощью параллельного переноса.
В курсе аналитической геометрии рассматриваются только свободные векторы.
Определение 2. Вектор, длина которого равна нулю, называется нулевым вектором, или ноль –
вектором.
Очевидно, начало и конец нулевого вектора совпадают. Нулевой вектор не имеет определенного направления или имеет любое направление.
Определение 3. Два вектора, лежащих на одной прямой или параллельных прямых называются
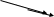 коллинеарными (рис.2). Обозначают:
коллинеарными (рис.2). Обозначают:
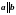 .
a
.
a
b
Нулевой вектор можно считать коллинеарным любому. рис.2
Определение 4. Два коллинеарных и одинаково направленных вектора называются
сонаправленными. Обозначают:
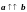 .
.
Теперь можно дать строгое определение равенства свободных векторов:
Определение 5. Два свободных вектора называются равными, если они сонаправлены и имеют
одинаковую длину.
Определение 6. Три вектора, лежащих в одной или параллельных плоскостях называются
компланарными.
Два
перпендикулярных вектора называют
взаимно ортогональными: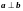 .
.
Нулевой вектор можно считать ортогональным любому.
Определение 7. Вектор единичной длины называется единичным вектором или ортом.
Орт, сонаправленный ненулевому вектору а называют ортом вектора а : ea .
§2. Линейные операции над векторами.
На множестве векторов определены линейные операции: сложение векторов и умножение вектора на число.
I. Сложение векторов.
Суммой 2 – х векторов называется вектор, начало которого совпадает с началом первого, а конец с концом второго, при условии, что начало второго совпадает с концом первого.
Л егко
видеть, что сумма двух векторов,
определенная
егко
видеть, что сумма двух векторов,
определенная
таким образом (рис.3а), совпадает с суммой векторов,
построенной по правилу параллелограмма (рис.6). b
Однако, данное правило позволяет строить a
сумму любого числа векторов (рис.3б).
a+b
рис.3а
 a
a
b a+b+c
рис.3б c
