Модуль 5 динамика жидкости введение

Динамика жидкости – раздел гидромеханики, который изучает законы движения жидкостей в зависимости от приложенных к ним сил.

При заданных внешних силах задача динамики жидкости сводится к определению напряжений и кинематических параметров движения в каждой точке жидкости в любой момент времени, а также к определению гидродинамических сил воздействия потока на тела.

В механике жидкости для облегчения решения некоторых задач используется понятие об идеальной жидкости.

Под идеальной жидкостью подразумевают такую условную жидкость, которая обладает абсолютной несжимаемостью, абсолютной подвижностью частиц, а также отсутствием сил сцепления между ними. Вязкость идеальной жидкости равна нулю. Таким образом, идеальная жидкость перемещается по трубам и каналам без сопротивлений (без потери энергии на трение). Когда реальная жидкость находится в покое, в ней не проявляются силы вязкости и она имеет свойства, близкие к свойствам идеальной жидкости. Следовательно, рассмотрение при решении гидравлических задач идеальной жидкости вместо реальной вполне допустимо. Такое рассмотрение позволяет применять точный математический анализ для решения технических задач в гидравлике.

Нормальные напряжения в движущейся идеальной жидкости обладают теми же свойствами, что и в покоящейся жидкости, то есть в данной точке их значения не зависят от направления действия. Таким образом, напряженное состояние движущейся невязкой жидкости может быть охарактеризовано в каждой точке значением нормального напряжения. Поскольку это значение не зависит от направления действия, его, как и при равновесии жидкости, называют давлением.

Основы научнотеоретических знаний по модулю

1. Дифференциальное уравнение движения невязкой жидкости в форме Эйлера

Для решения задачи о движении невязкой жидкости нужно составить уравнения движения, связывающие между собой скорости, давления и массовые силы, действующие в жидкости.

Чтобы получить эти уравнения, используем векторное уравнение движения жидкости, выраженное через напряжения

В невязкой жидкости действуют только нормальные напряжения, связь которых с давлениями имеет вид:

Подставляя эти значения в уравнение в напряжениях, получим уравнение:

,

Или используя понятие градиента скалярной функции P

(5.1)

Полученное уравнение называется дифференциальным уравнением движения невязкой жидкости в форме Эйлера.

Получим уравнение в скалярной форме, спроецировав его на оси координат:

(5.2)

В уравнениях Эйлера считаются известными плотность и вектор напряжения массовых сил , и . Искомыми в этих уравнениях являются три проекции скорости , , и давления , т.е. четыре неизвестных функции. Чтобы привести в соответствие число уравнений и число неизвестных, к уравнениям Эйлера (5.2) следует добавить уравнение неразрывности

2. Интеграл Бернулли для линии тока

В общем случае уравнение движения жидкости не интегрируются. Для частных случаев их интегрирование возможно, если принять некоторые допущения.

Рассмотрим случай установившегося движения вдоль линии тока. В этом случае режим движения жидкости в каждой точке пространства не изменяется с течением времени. Линии тока при установившемся движении совпадают с траекториями жидких частиц.

Умножая скалярно основное уравнение движения:

на элементарное перемещение жидкой частицы вдоль линии тока получаем:

Или

.

Так как при установившемся движении , то выражение является полным дифференциалом и можно написать:

Это уравнение может быть проинтегрировано при соблюдении двух условий:

1. Если массовые силы имеют потенциал.

2. Если жидкость баротропная, т.е. ее плотность зависит только от давления.

По первому условию:

; ; и .

или .

Это уравнение можно интегрировать, где интегралом будет

(5.3)

Полученное уравнение называется интегралом Бернулли. Константа в правой части постоянна только вдоль линии тока. При переходе к другим линиям тока значение постоянной в интеграле Бернулли изменяется.

Рассмотрим наиболее важный частный случай, когда в жидкости действует сила тяжести, т.е. , и запишем для него интеграл уравнения движения. Одновременно умножим обе части уравнения на плотность и учтем, что .

Тогда получим:

(5.4)

Интеграл Бернулли в такой записи часто называют уравнение Бернулли.

Все члены, входящие в это уравнение, имеют размерность давления.

Три формы уравнения Бернулли:

– 1-ая форма уравнения Бернулли в напорах;

– 2-ая форма уравнения Бернулли в давлениях;

– 3-я форма уравнения Бернулли в квадратах скоростей.

Рассмотрим энергетический смысл уравнения Бернулли.

Рассмотрим частицу жидкости, с массой , которая движется вдоль линии тока. Определим величину полной энергии, которой обладает частица сеч. I и II. Кинетическая энергия соответственно и . Потенциальная энергия равна весу частицы на высоту подъема ее. В сеч. I высота подъема ; в сеч. II  .

В сеч. I потенциальная энергия

,

где  объем частицы;

 объемный вес.

Потенциальная энергия частицы может быть записана

,

Так как .

А ,

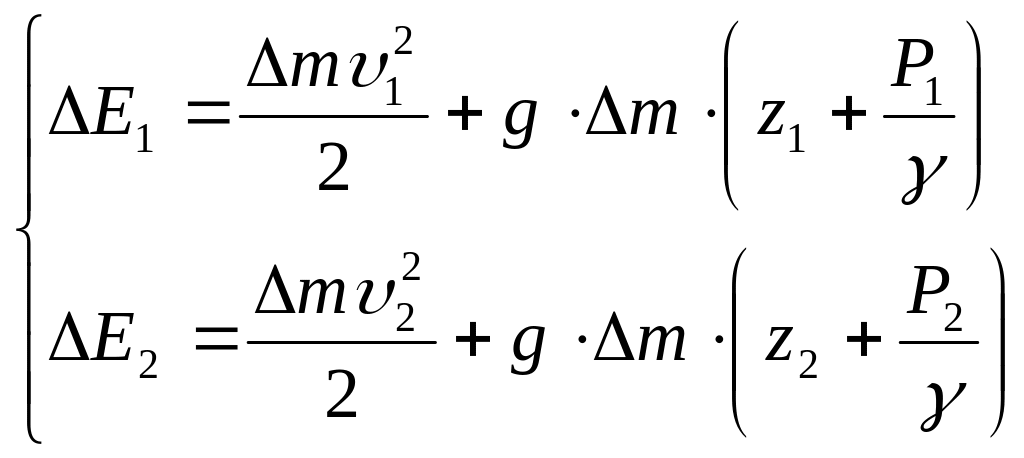где  полная энергия частицы в сеч. I;

 полная энергия частицы в сеч. II;

Разделив почленно на вес частицы , определим полную энергию, которая заключается в единице веса жидкости. Это удельная энергия ( ).

Удельная энергия, отнесенная к ед. веса ,

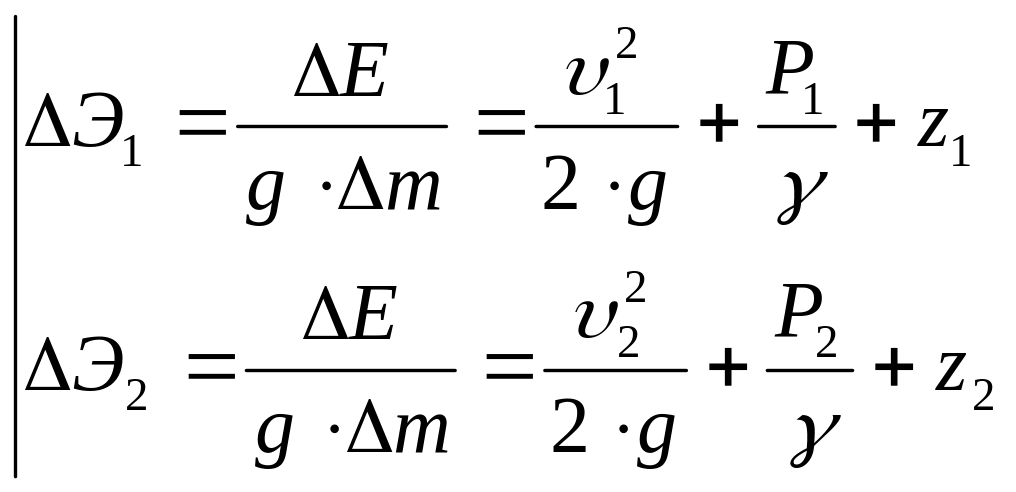где и  удельная кинетическая энергия;

и  удельная потенциальная энергия давления;

и  удельная потенциальная энергия положения.

Разделим уравнения (А) на единицу объема.

Уравнения (А) перепишутся:

; делим на

 в давлениях.

Разделим уравнения (А) на единицу массы и поучим:

Поскольку сумма кинетической и потенциальной энергии равна полной механической энергии, интеграл Бернулли можно истолковать следующим образом: вдоль линии тока механическая удельная энергия частицы жидкости постоянна. Это есть одно из выражений закона сохранения энергии, который в данных условиях выражается интегралом Бернулли.

Весьма часто в практических задачах представляет интерес не все давление , а лишь гидродинамическая добавка к нему, вызванная движением жидкости, т.е. так называемое избыточное гидродинамическое давление.

Рассмотрим, например, поток со свободной поверхностью, которую примем за плоскость сравнения. Гидростатическое давление равно . Введем избыточное гидродинамическое давление как разность между давлением в этой точке и гидростатическим давлением:

.

Подставляя выражение для в уравнение (5.4), приведем его к виду:

Из этого выражения следует, что в тех точках потока, где скорость больше, давление уменьшается.