3.2.1.2 Исследование моделей авторегрессии пиковой нагрузки
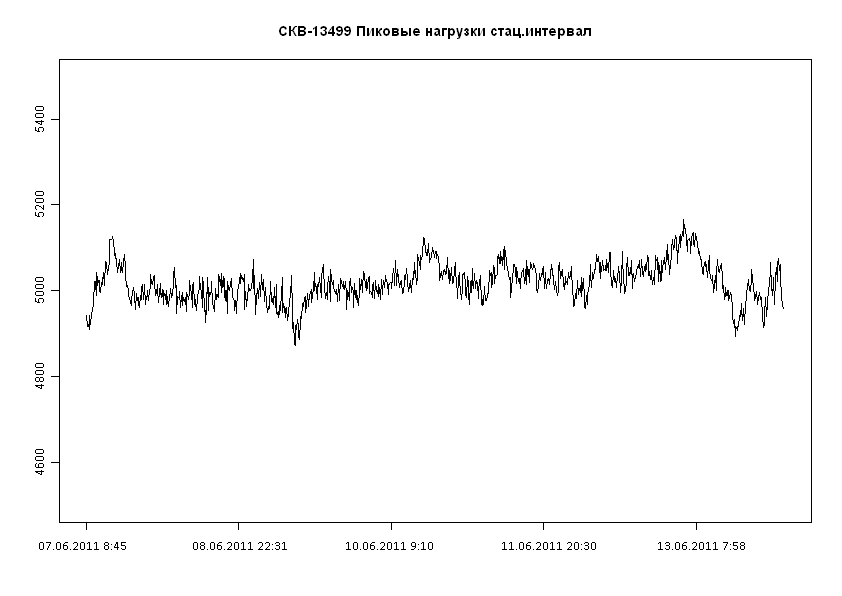
В соответствии с описанной выше методикой анализа временных рядов, проведен статистический анализ отрезка траектории параметра пиковой нагрузки, который визуально стационарны, на примере скважины 13499. График траектории этого участка приводится на рис. 3.7.
Уравнения авторегрессии для стационарного участка имеют вид:
АR(2): |
Xt=0.601Xt-1+0.399Xt-2 |
(3.3) |
АR(3): |
Xt=0.552Xt-1+0.327Xt-2+0.121Xt-3 |
(3.4) |
Модель
авторегрессии второго порядка.
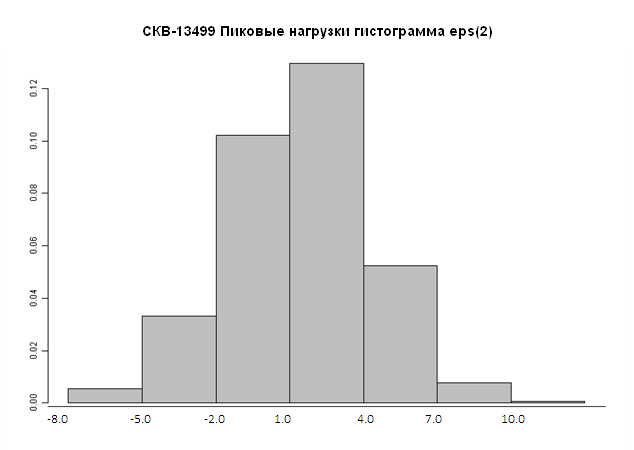
На рис. 3.8 приводится гистограмма невязок
для AR(2),
относящаяся к участку стационарности.
Стационарный участок характеризуется
следующими оценками основных характеристик
невязок
:
выборочное среднее 
=0.00697,
стандартное отклонение σ=142.0,
выборочный коэффициент асcиметрии
γ1=-10.6
и эксцесса γ
2=128.0.
|
Рисунок 3.7 – Временная траектория стационарного участка пиковой нагрузки на скважине 13499.
|
|
Рисунок 3.8 – Гистограмма невязок модели авторегрессии AR(2) стационарного участка пиковой нагрузки на скважине 13499.
|
Для модели AR(2) при выборке объемом 1466 значение критерия χ2(2)= 162.0. При этом критический уровень значимости р<10-3,
Проверка на нормальность с помощью критерия хи-квадрат указывает на высокую значимость отклонения от нормальности; хотя эмпирические значения результатов прогноза, представленные на следующих графиках, показывают хорошее согласие с реальными данными.
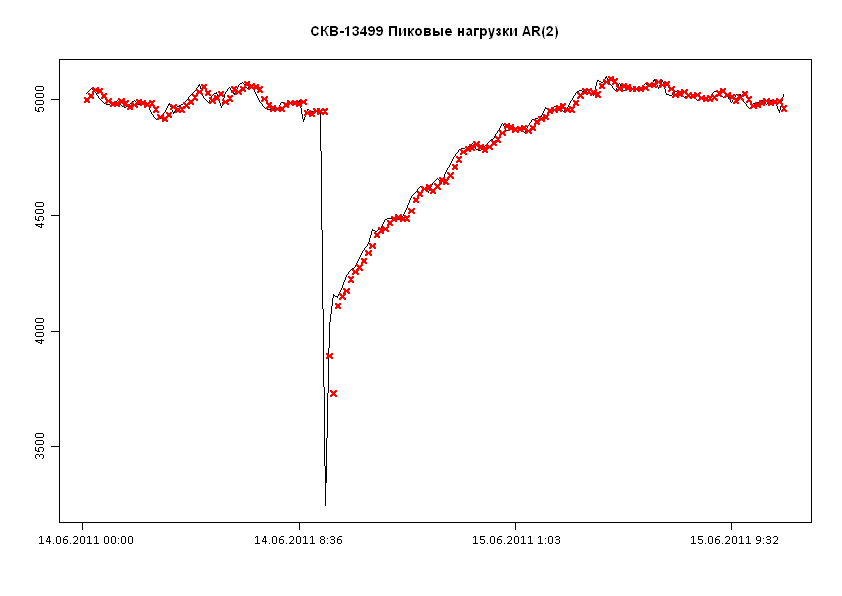
На рис. 3.9 представлен фрагмент участка исходной траектории, выбранный в момент времени, близкий к разладке (рис. 3.6, область II). Результаты указывают на хороший прогноз кривой авторегресси на участке, где нет резких скачков значений пиковой нагрузки.
|
Рисунок 3.9 – Модель авторегрессии второго порядка для пиковой нагрузки на скважине 13499. Сплошная кривая – фактические показатели, крестики – прогноз по модели AR(2)
|
В то же время на данном участке явно имела место разладка: резкое падение пиковой нагрузки. Об этом же говорят результаты прогноза. Прогнозируемое значение пиковой нагрузки равно 4950; фактическое значение 3240. Разность, равная 1710, много больше значения 3σ=3∙142=426.
Необходимо отметить, что никаких признаков наступления разладки процесс авторегрессии не обнаруживает. Произошло резкое падение (обрушение) пиковой нагрузки без каких-либо предварительных сигналов. Лишь непосредственно перед самой разладкой значение пиковой нагрузки непродолжительное время было практически постоянным.
Более того, сравнение с журналом простоев, выдержка из которого приведена в табл. 2.1, показывает, что в моменты разладки насос не останавливался.
Модель авторегрессии третьего порядка. Аналогичным образом проведены расчеты модели AR(3) для пиковой нагрузки на сквадине 13499.
Гистограмма невязок для участка стационарности приведена на рис. 3.10. Статистические оценки основных характеристик невязок следующие: выборочное среднее =0.211, стандартное отклонение σ=140.0, выборочный коэффициент асcиметрии γ1=-11.3 и эксцесса γ2=136.0. Выборка объема 2126, критерий критерия χ2(3)= 161.0, критический уровень значимости р<10-3. Проверка на нормальность с помощью критерия хи-квадрат по прежнему указывает на высокую значимость отклонения от нормальности.
|
Рисунок 3.10 – Гистограмма невязок модели авторегрессии AR(3) стационарного участка пиковой нагрузки на скважине 13499.
|
На рис. 3.11 представлены прогнозные значения пиковой нагрузки согласно модели авторегресии AR(3). Результаты расчетов показывают, что модель авторегрессии третьего порядка дает более точный прогноз на участке стационарности. Однако, точно также, как и модель авторегрессии второго порядка, момент разладки наступает «неожиданно».