6. Розрахункове завдання №5

Тема: розрахунок множинних і часткових коефіцієнтів кореляції

Мета: надбання навичок розрахунку множинних і часткових коефіцієнтів кореляції.

1. Основні теоретичні положення

Багатофакторна економетрична модель містить одну результативну ознаку (у) і m факторних ознак (х₁, х₂, …, х_m). Між кожною парою ознак існує кореляційний зв'язок, який можна вимірити кількісно парним коефіцієнтом кореляції

, ;

, .

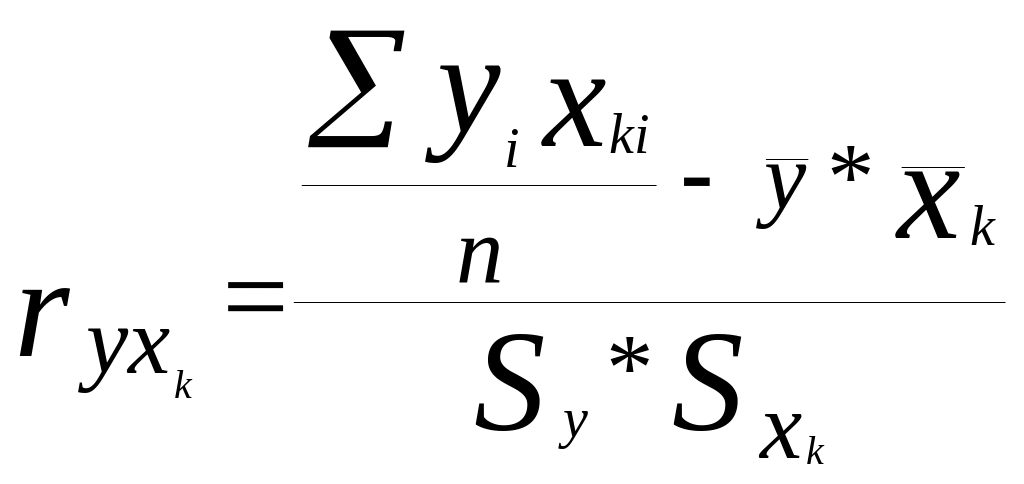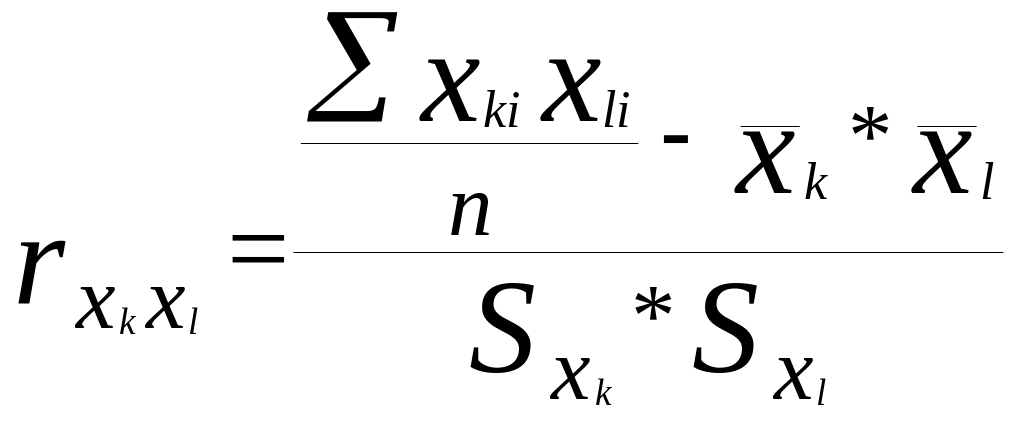З цих коефіцієнтів кореляції можна скласти кореляційну матрицю

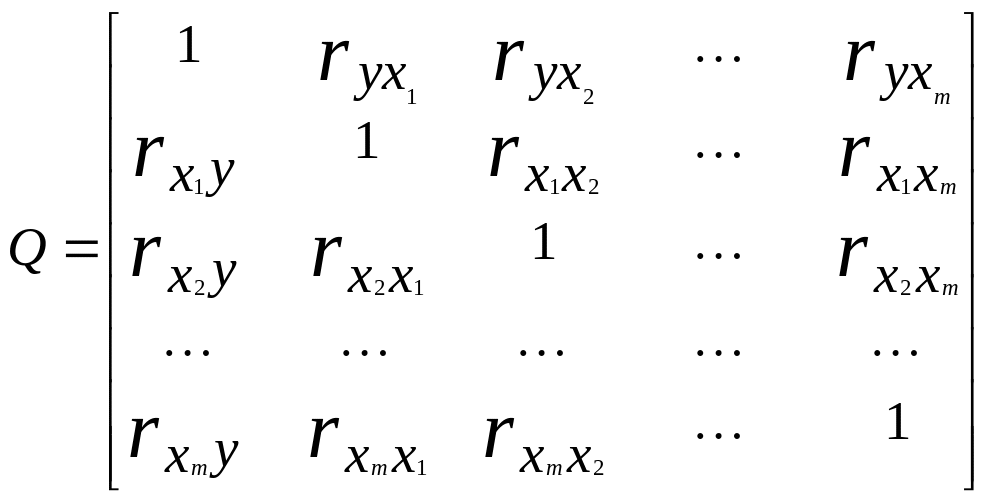
Під час побудови цієї матриці керуються таким правилом:

• ознаки нумерують в такому порядку:

у	х1	х2	…	хm ,
1	2	3	…	m+1 ;

Таким чином, i-ому рядку (стовпцю) відповідає (i–1)-а факторна ознака х_i-1;

• на перетинанні i-ого рядка і j-го стовпця поміщаємо коефіцієнт кореляції між (i-1)-ою і (j-1)-ою ознаками.

Коефіцієнтам кореляції притаманні дві основні властивості:

1. коефіцієнт кореляції ознаки із самою собою дорівнює 1.

; .

Дійсно,

.

Аналогічно для ;

2. значення коефіцієнта кореляції не залежить від порядку проходження ознак ; .

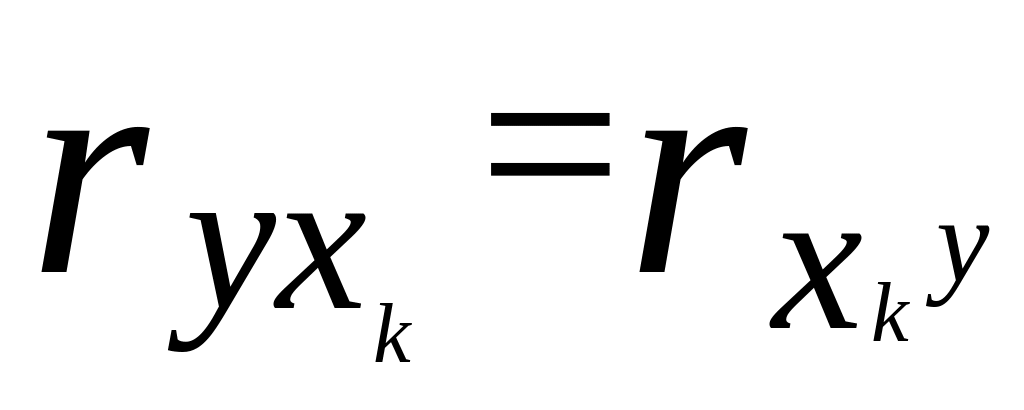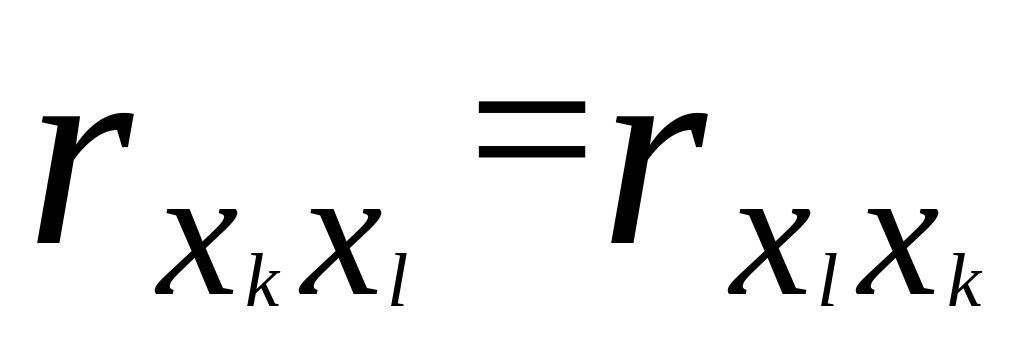Ця властивість випливає з формули коефіцієнта кореляції, у якій зміна порядку проходження ознак приводить до перестановки співмножників, від чого добуток не змінюється.

З цих двох властивостей коефіцієнтів кореляції випливають такі властивості кореляційної матриці:

1. елементи головної діагоналі кореляційної матриці дорівнюють 1;

2. матриця симетрична щодо головної діагоналі, тобто не змінюється при транспонуванні.

Таким чином, в остаточному виді кореляційну матрицю можна записати так:

.

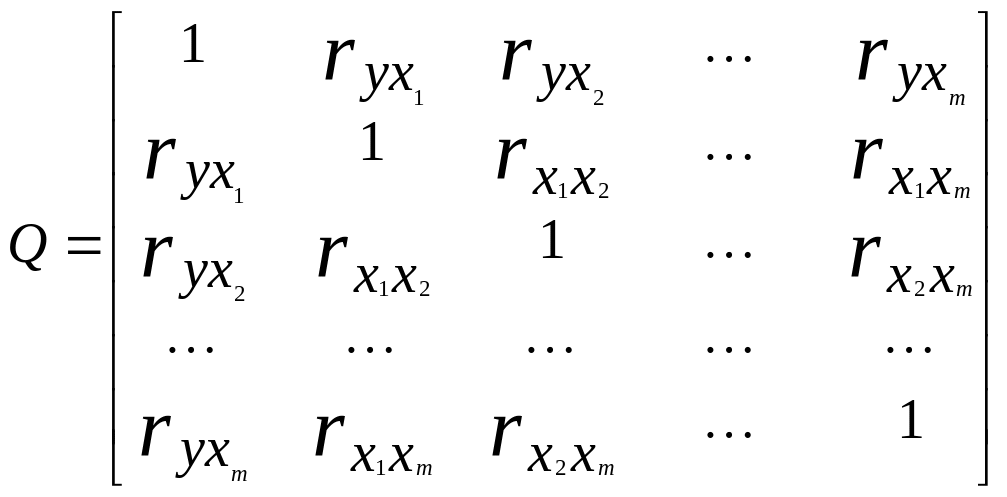Множинний коефіцієнт детермінації визначає частку варіації результативної ознаки (у), що пояснюється варіацією всієї сукупності факторних ознак (х₁, х₂, …, х_m). Обчислюють множинний коефіцієнт детермінації за формулою

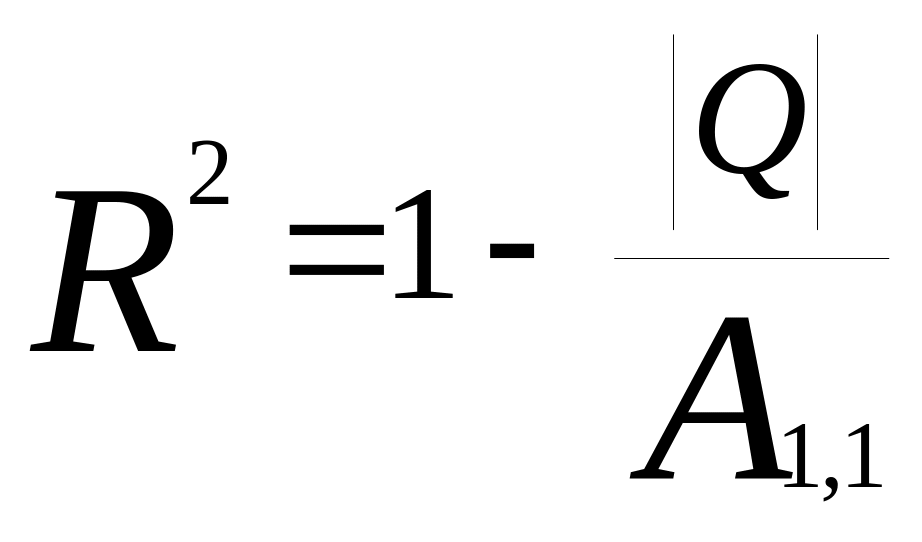, (1)

де – визначник кореляційної матриці;

А_1,1 – алгебраїчне доповнення до елемента матриці, що знаходиться на перетинанні 1-ого рядка і 1-го стовпця.

Алгебраїчне доповнення A_i,j обчислюється за такою формулою

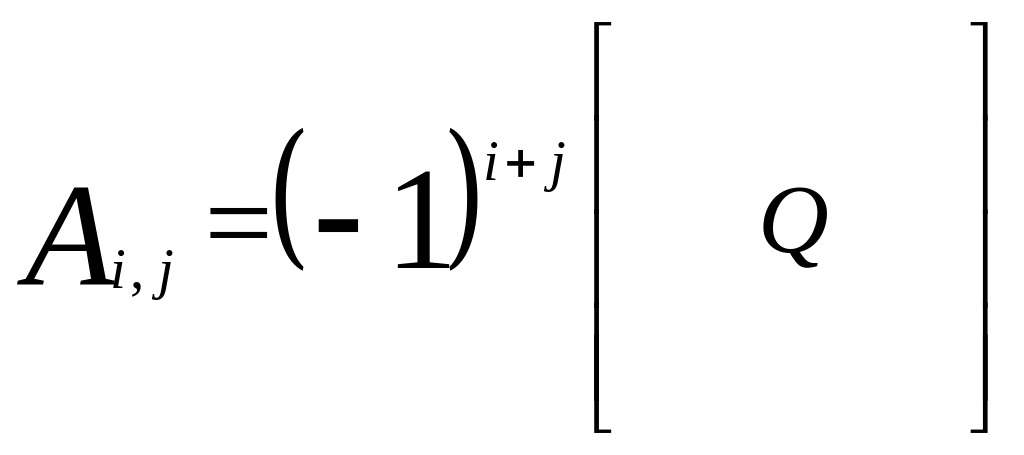
i,

j

тобто алгебраїчне доповнення A_i,j обчислюється з визначника кореляційної матриці, у якій викреслені i-ий рядок і j-ий стовпець.

Множинний коефіцієнт кореляції R вимірює тісноту кореляційного зв'язку результативної ознаки (у) із усією сукупністю факторних ознак (х₁, х₂, …, х_m)

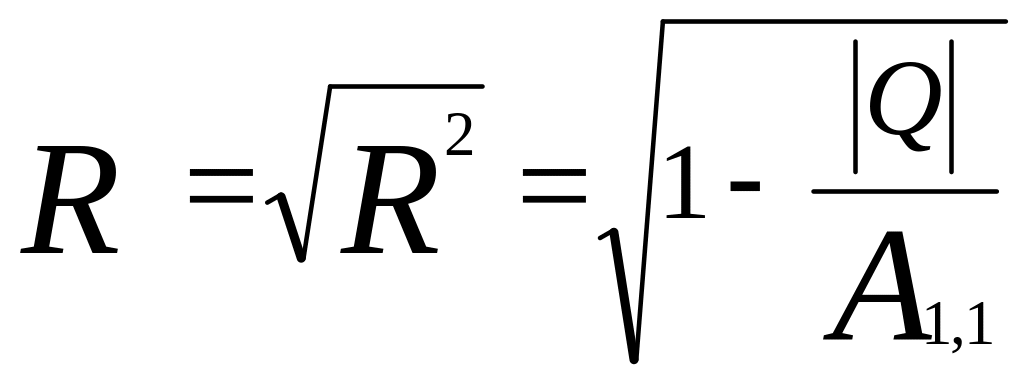. (2)

При обчисленні парних коефіцієнтів кореляції передбачається, що вся зміна у викликана впливом фактора x_k. У дійсності це не так, оскільки на зміну у крім x_k впливають і інші ознаки. Тому істинну тісноту кореляційного зв'язку між у і кожною з факторних ознак (х₁, х₂, …, х_m) у випадку множинної кореляції виміряється частковими коефіцієнтами кореляції

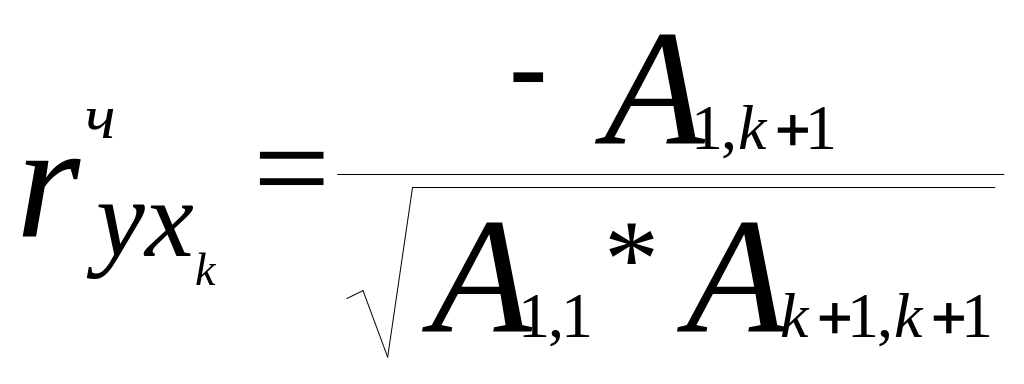. (3)

При розрахунку поодиноких коефіцієнтів кореляції за допомогою Excel можна використовувати і метод, що заснований на обчисленні зворотної матриці. Дійсно, якщо

,

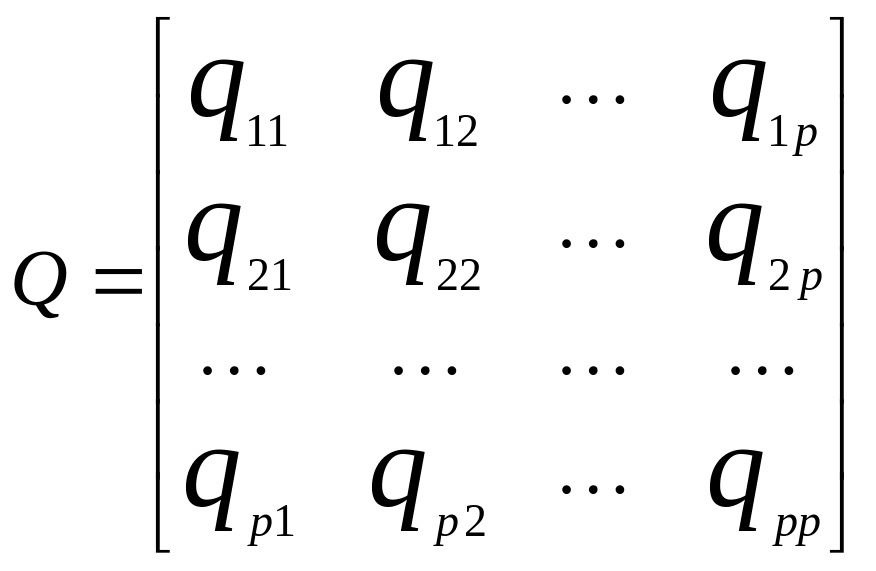д е p=m+1, то зворотна матриця буде дорівнювати

,

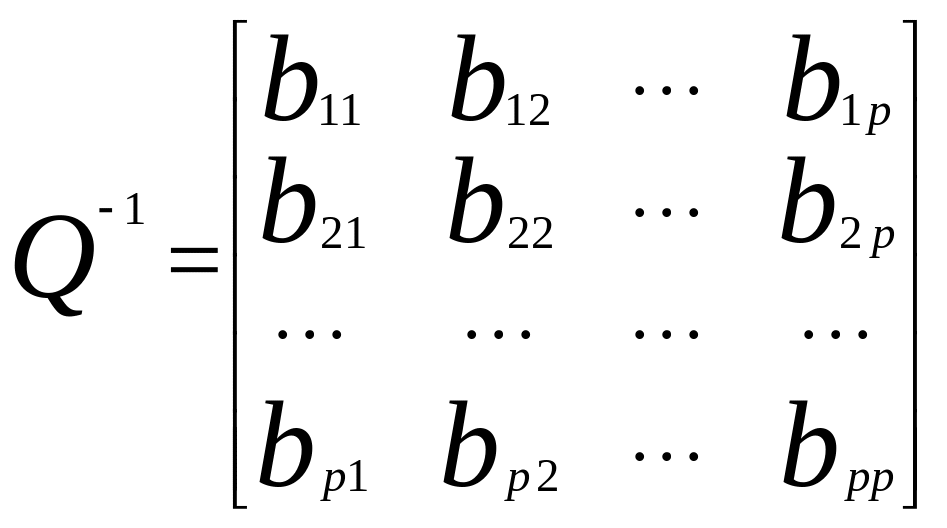де 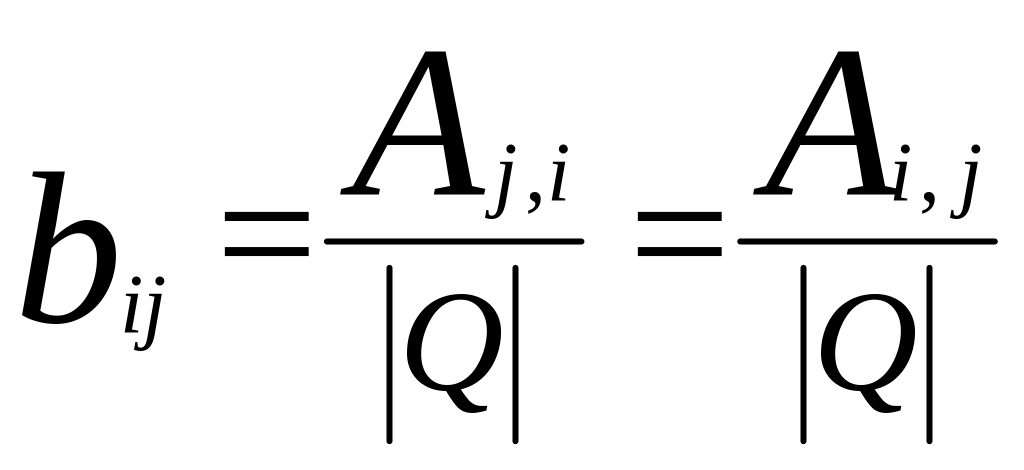. Остання рівність пояснюється симетричністю кореляційної матриці.

Тоді поодинокий коефіцієнт кореляції

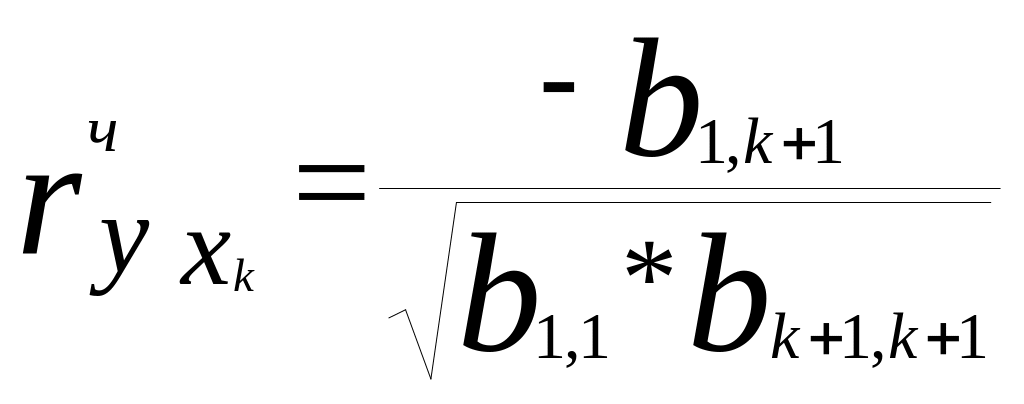, (4)

що еквівалентно формулі (2), тому що

.

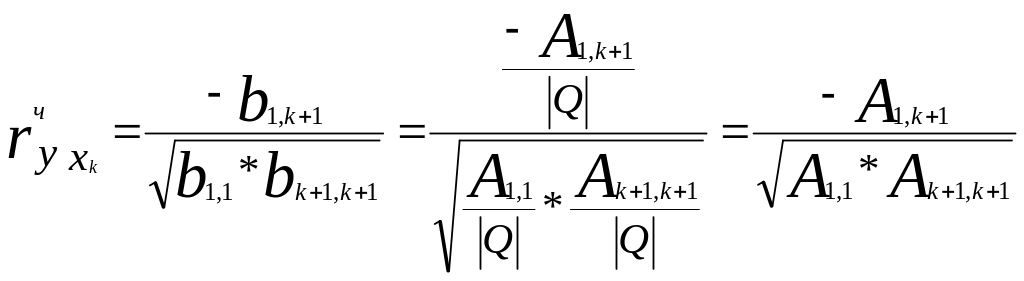Таким чином, існує два такі способи розрахунку часткових коефіцієнтів кореляції:

1. розрахунок за формулою (2).

2. розрахунок матриці, зворотної до кореляційної матриці, і обчислення за формулою (3).