Раздел 3. Интегральное исчисление

§ 3.1. Первообразная

1. Определение первообразной функции

2. Неоднозначность нахождения первообразной

1. Определение первообразной функции

Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.

Определение. Дифференцируемая функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство F'(x) = f(x).

Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной.

Так, функция F(x) = х² есть первообразная функции f(х) = 2х на интервале (- ∞; ∞), поскольку для всех х имеет место равенство F'(x) = (х²)'= 2х.

1) Найти первообразную функции f (х) = 4 x 3. Решение. Используя правило дифференцирования, можно догадаться, что на интервале (- ∞; ∞) первообразной является F(x) = x 4. Действительно, F'(х) = 4x3 для всех Замечание. Если сказано, что F(x) — первообразная функции f(x), но не указано, в каком именно интервале, то под этим интервалом в даль­нейшем будет подразумеваться любой интервал, в котором функция f(x) определена. 2) Даны пары функций, из которых вторая должна быть первообразной для первой: а) х4 и х:5; б) 5cos5x и sin5x; в) Зе3х и е3х; г) и ctg2x; д) и arctg3x. В каких примерax допущены ошибки?

2. Неоднозначность нахождения первообразной

Как всякое обратное действие, интегрирование вносит некоторое осложнение. Вспомним, как начинается изучение действий над числами. Сначала изучают только целые положительные числа. Наиболее простое действие — сложение — не вносит никаких затруднений. Однако стоит только перейти к обратному действию вычитанию, как встречается первое затруднение: вычесть из меньшего числа большее невозможно. Чтобы преодолеть эту трудность, в алгебре вводят отрицательные числа и вычитание становится возможным, например 1-3 = - 2. При умножении целых чисел не встречается никаких затруднений; обратное же действие - деление - сразу вносит трудность. Оказывается, что далеко не все числа делятся друг на друга. Деление становится возможным с введением дробных чисел, например 9:4 = 2,25. Еще большие затруднения появляются при извлечении корня -действии, обратном возведению числа в целую положительную степень; здесь уже появляются затруднения в знаках. Так, корень четной степени из положительного числа имеет два знак, а корень четной степени из отрицательного числа не имеет дей­ствительного значения. Чтобы стало возможным извлечение корней целой положительной степени из действительных чисел, требуется ввести понятия об иррациональном числе, о мнимой единице, о мнимом числе и т. д. Интегрирование как действие, обратное дифференцированию, также вносит осложнение.

Дифференцирование функции - однозначная операция, так если функция имеет производную, то только одну. Это утверждение непосредственно следует из определений предела и производной: если функция имеет предел, то только один. Обратная операция — отыскание первообразной — не однозначна.

Так, функции F₁ (x)=x⁴, F₂(х) = х⁴ + 5, F₃(x) = х⁴ - , F₄ (x) = х⁴+C, где С - любое постоянное действительное число, являются первообразными функции f(x) = 4x³, , поскольку все эти функции имеют одну и ту же производную 4х³.

Теорема. Если F(x) является первообразной функции f (x) на некотором промежутке, то множество всех первообразных этой функции имеет вид F(x) + C, где С — любое действительное число.

Д о к а з а т е л ь с т в о. Пусть F'(x) = f(x). Тогда (F(x)+ C)'= F'(x) + C'= F'(x) = f(x).

Покажем теперь, что все первообразные функции f(x) отличаются лишь постоянным слагаемым.

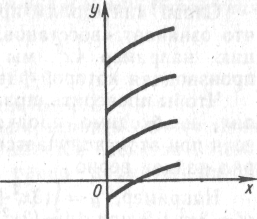
Пусть Ф(х) - другая первообразная функции f(x) на рассматриваемом промежутке, т.е. Ф'(x) = f(x).Тогда (Ф(х)-F(х))' = Ф'(х)-F'(x)= f(x) - f(x) = 0 при всех х из рассматриваемого промежутка. Следовательно, Ф(х) - F(х) = С, что и требовалось установить.

Таким образом, любые две первообразные данной функции отличаются друг от друга на постоянное слагаемое, а выражение F(x)+C исчерпывает множество всех первообразных заданной функции f(x). Итак, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений.

Геометрически выражение F(x)+C представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси Оу (рис. 1).