
Задание 3
Мебельная фабрика выпускает стулья двух типов (стоимостью 80 и 120 руб.) На изготовление каждого стула расходуются доски стандартного сечения, обивочная ткань и рабочее время.
Какое количество стульев каждого типа нужно изготовить, чтобы прибыль фабрики была максимальной? Данные о запасах и расходах сырья приведены в таблице ниже.
Таблица
Используемые ингредиенты |
Расход ингредиентов на изготовление одного стула |
Кол-во ингредиентов в распоряжении фабрики |
|
1 типа |
2 типа |
||
Доски, м |
2 |
4 |
440 |
Обивочная ткань, м |
0,5 |
0,25 |
65 |
Рабочее время, чел./час |
2 |
2,5 |
320 |
Стоимость, руб. |
80 |
120 |
max |
Решение:
Введем обозначение проектных параметров:
– число изготовленных стульев 1-го типа;
– число изготовленных стульев 2-го типа.
Запишем математическую модель задачи.
Определим такой вектор продукции , который удовлетворяет условиям:

и обеспечивает максимальное значение целевой функции прибыли:
![]() .
.
Последняя строка ограничений говорит о невозможности производить отрицательное количество продукции.
2)
Найдем решение поставленной задачи линейного программирования при помощи пакета MS Excel. Для этого откроем новый лист «Задание3».
В ячейки
![]() листа «Задание 3» запишем коэффициенты
при неизвестных наших полученных
ограничений, т.е. расходы сырья на
производство единицы продукции. В ячейки
листа «Задание 3» запишем коэффициенты
при неизвестных наших полученных
ограничений, т.е. расходы сырья на
производство единицы продукции. В ячейки
![]() занесем значения правых частей неравенств
ограничений, т.е. запасы ресурсов. В
ячейки
занесем значения правых частей неравенств
ограничений, т.е. запасы ресурсов. В
ячейки
![]() запишем начальное значение искомых
параметров
и
.
Ячейки
запишем начальное значение искомых
параметров
и
.
Ячейки
![]() содержат значения ограничений при
заданных значениях неизвестных, т.е.
формулы: =$B$14*B3+$C$14*C3. В
ячейки
содержат значения ограничений при
заданных значениях неизвестных, т.е.
формулы: =$B$14*B3+$C$14*C3. В
ячейки
![]() запишем параметры целевой функции:
коэффициенты при неизвестных, т.е.
прибыль от реализации единицы продукции.
Саму целевую функцию поместим в ячейку
запишем параметры целевой функции:
коэффициенты при неизвестных, т.е.
прибыль от реализации единицы продукции.
Саму целевую функцию поместим в ячейку
![]() :
=$B$14*$B$10+$C$14*$C$10.
:
=$B$14*$B$10+$C$14*$C$10.
Для удобства сведем все неравенства ограничения к одному знаку:
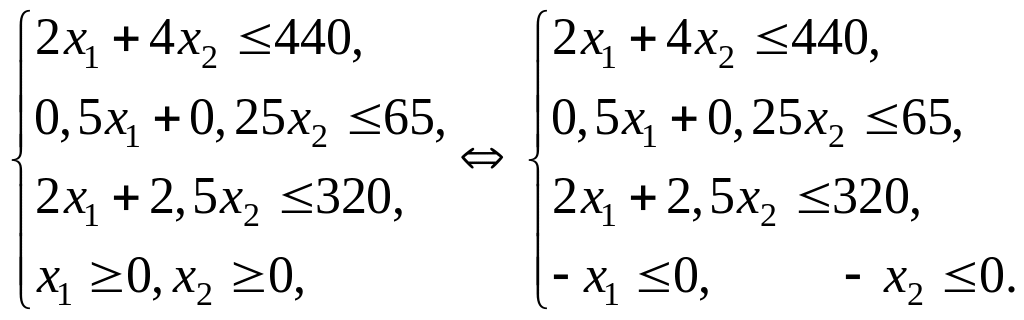
После заполнения таблицы необходимыми
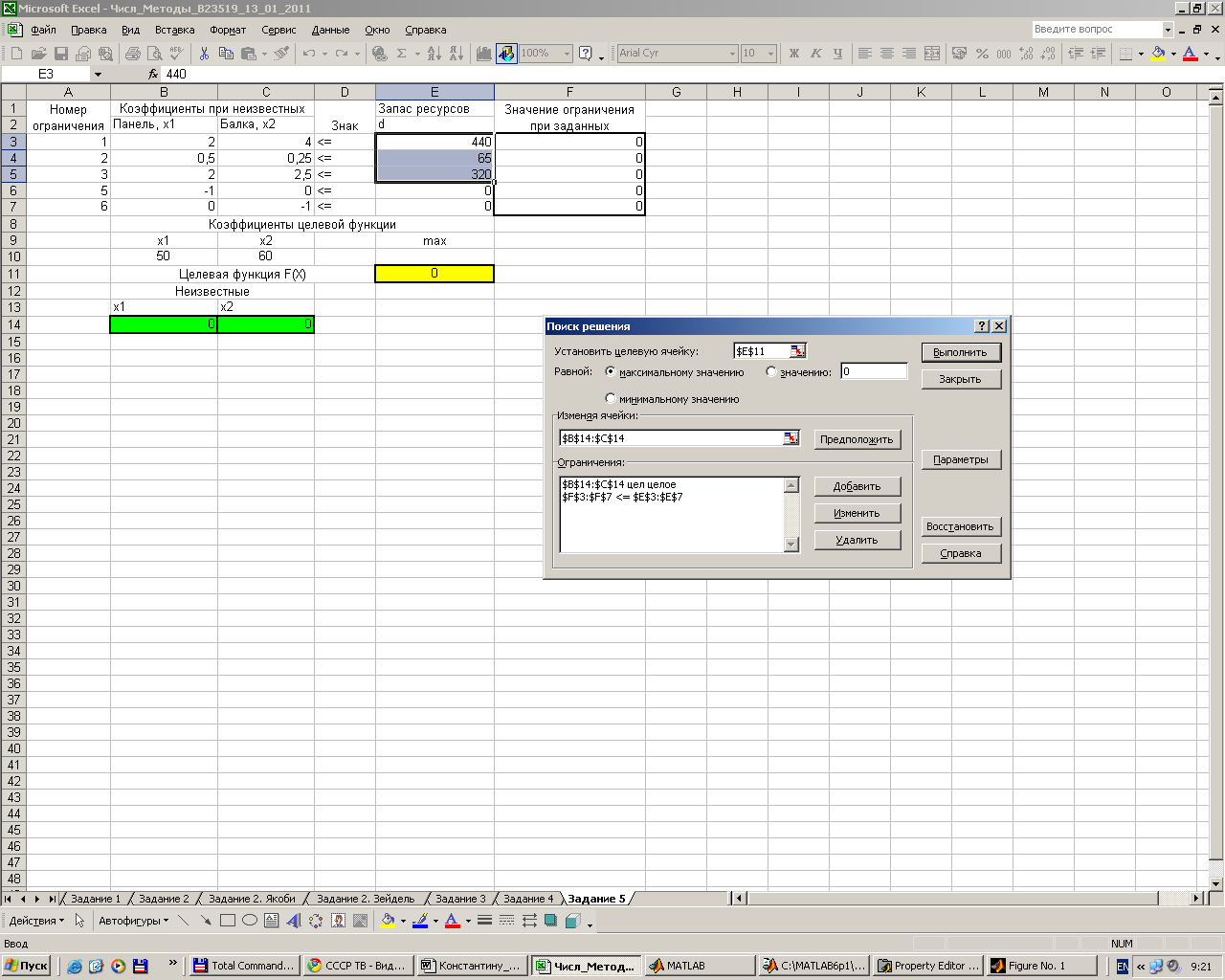
исходными данными запускаем надстройку
«Поиск решения». В появившемся окне в
качестве целевой ячейки установим
ячейку
,
укажем, что она должна быть равна
максимальному значению. Изменяемыми
ячейками являются те, что содержат
начальное значение неизвестных, т.е.
.
Кроме того, необходимо «Добавить»
ограничения. Т.к. ограничения имеют
одинаковые знаки, то их добавление можно
проделать в одну строчку –
![]() .
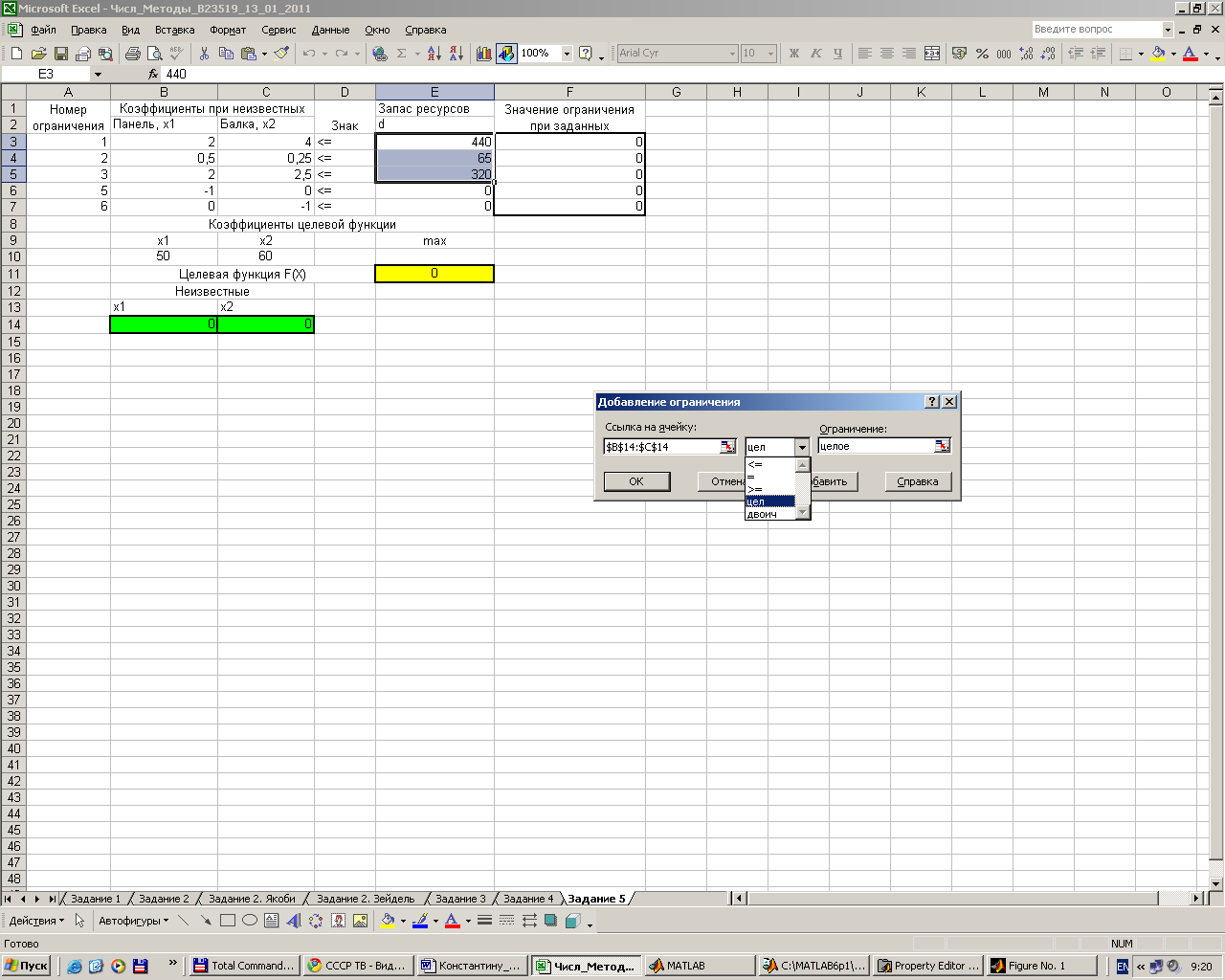
Однако, учитывая экономическую особенность
задачи необходимо поставить ограничение
на целочисленное значение искомых
решений (стулья нельзя производить и
продавать нецелыми) –
цел целое.
.
Однако, учитывая экономическую особенность
задачи необходимо поставить ограничение
на целочисленное значение искомых
решений (стулья нельзя производить и
продавать нецелыми) –
цел целое.
После установления всех необходимых
параметров поиска нажимаем кнопку
«Выполнить». Сохраняем результаты
поиска решения (никаких отчетов делать
необязательно). В результате получаем,
что максимальное значение целевой
функции, т.е. прибыли, составит
![]() руб.
и будет достигнуто при производстве
руб.
и будет достигнуто при производстве
![]() ед. стульев 1-го типа и
ед. стульев 1-го типа и
![]() ед. стульев 2-го типа. При этом все
ограничения будут выполняться.
ед. стульев 2-го типа. При этом все
ограничения будут выполняться.
Итак, решение поставленной экономической задачи линейного программирования найдено!
