2.5 Определение значений коэффициентов важности показателей свойств
После выбора целого ряда свойств, по которым будет проходить оценка качества товара, возникает проблема как же их уравновесить и привести к общим единицам измерения. Ведь такие свойства как, например твердость и шероховатость различаются как по смыслу и своей важности для изделия, так и по единицам измерения. Именно для этого и проводиться составление коэффициентов важности для каждого из выделенных свойств. Этим занимается экспертная группа, которая не только выделяет сами свойства, но и ее участники путем голосования и ранжирования присваивают каждому из свойств определенный номер, соответствующий по их мнению важности данного свойства в общем списке. По окончанию такого голосования результаты просматриваются, и производиться несложный расчет. Ведущий анализирует числа, записанные в анкету, с точки зрения максимальной величины расхождения между отдельными назначенными экспертами оценками. Величину расхождения мнений экспертов можно определить, используя коэффициент конкордации WN для N экспертов по формуле
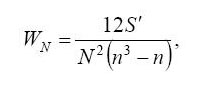
(1)
где S′ – сумма квадратов отклонений;
n – число показателей свойств в группе.
Сумма квадратов отклонений рассчитывается по формуле:
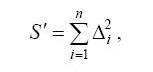
(2)
где Δi – отклонение от средней суммы рангов.
О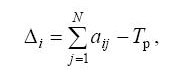
тклонение
от средней суммы рангов можно подсчитать
по формуле
(3)
где aij – ранг i-го объекта у j-го эксперта;
Тр – средняя сумма рангов.
Средняя сумма рангов определяется выражением
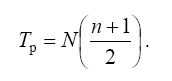
(4)
Если крайние значения между отдельными назначенными экспертами оценками отличаются друг от друга не более чем на 25 %, то опрос экспертов можно ограничить одним туром.
В данной работе мера согласованности определяется коэффициентом конкордации.
При WN ≥ 0,75 работа экспертов считается достаточно согласованной и следующий тур не нужен.
При расчете показателей, озвученных выше, в рамках данной курсовой работы были получены следующие результаты:
Таблица 3 - Промежуточные результаты вычислений коэффициента конкордации.
Номер свойства |
Тр |
∆i |
Sۥ |
WN |
1 |
36 |
20 |
400 |
0.99 |
2 |
4 |
16 |
||
3 |
-27 |
729 |
||
4 |
-21 |
441 |
||
5 |
28 |
781 |
||
6 |
2 |
4 |
||
7 |
13 |
169 |
||
8 |
12 |
144 |
Как можно увидеть из таблицы 3 WN =0,99. Из чего можно сделать вывод, о ненадобности 2 тура, и можно приступить к обработке результатов экспертного опроса (таблица 4).
Для каждого помещенного в сводной таблице 4 свойства вычисляют среднее арифметическое (по всем экспертам) значение ненормированного коэффициента весомости по результатам последнего тура
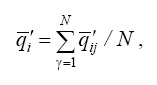
(5)
где qij′ – ненормированный коэффициент весомости для i-го свойства у j-го эксперта;
N – число экспертов.
Для каждой группы свойств определяется сумма А всех средних значений ненормированных коэффициентов весомости (с учетом всех свойств групп). Полученные числа заносят в сводную таблицу (таблица 4).
Таблица 4 - Результаты определения коэффициентов важности показателей свойств
Номер свойства |
q′ij |
Вычисление значений групповых коэффициентов |
||||||||||||||
1-й тур |
q′i |
А |
qi |
∑qi=1 |
||||||||||||
1 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
35 |
0,2 |
1 |
||||
2 |
4 |
4 |
4 |
2 |
4 |
4 |
4 |
6 |
3 |
0,085 |
||||||
3 |
1 |
1 |
1 |
5 |
1 |
1 |
1 |
1 |
1,5 |
0,042 |
||||||
4 |
2 |
2 |
2 |
1 |
2 |
2 |
2 |
2 |
1,875 |
0,055 |
||||||
5 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
0,228 |
||||||
6 |
5 |
5 |
5 |
4 |
5 |
5 |
5 |
4 |
4,75 |
0,136 |
||||||
7 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
5 |
5,875 |
0,167 |
||||||
8 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
0,086 |
||||||