
- •Неустойчивость плазмы.
- •Условия устойчивости плазмы
- •, Где (радиус Бора) - условие неквантованности плазмы.
- •Плазма во внешних полях. Плазма во внешнем однородном электрическом поле.
- •Плазма во внешнем переменном электрическом поле.
- •Плазма во внешнем однородном магнитном поле.
- •Если частица движется перпендикулярно н, то .
- •Плазма в комбинированных полях.
- •Взаимодействие плазмы и полей.
- •Явление переноса частиц в плазме. Перенос под действием электрического поля.
- •1. Полностью ионизованная плазма.
- •2 Слабоионизованная плазма.
- •Перенос под действием градиента концентрации частиц.
- •Перенос под действием градиента температуры
- •Процессы переноса в магнитном поле.
- •Образование активных частиц плазмы.
- •Условные обозначения:
- •Элементарные процессы в плазме
- •Ионизация
- •Диссоциация
- •Тройная рекомбинация электронов и ионов.
- •Модель процесса плазмохимической обработки.
2 Слабоионизованная плазма.
В
этом случае
![]() ,
a
,
a
![]() т.к. Ni
=
min
и
т.к. Ni
=
min
и
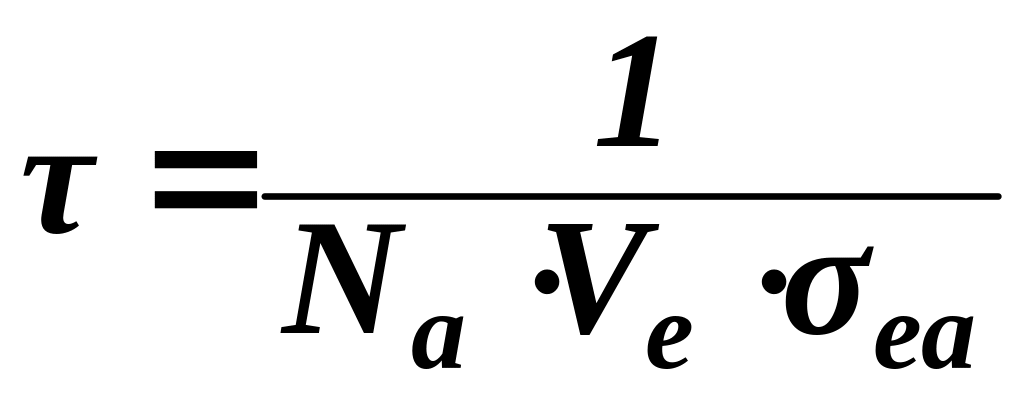 ,
где
,
где
![]() –
эффективное
сечение столкновения электронов с
атомами. Тогда:
–
эффективное
сечение столкновения электронов с
атомами. Тогда:
![]() ,
(19)
,
(19)
где
![]() - степень ионизации;
- степень ионизации;
![]() ‑ средние
значения с учетом распределения
электронов по скоростям и зависит
‑ средние
значения с учетом распределения
электронов по скоростям и зависит
![]() от
от
![]() .
.
Из
(19)
следует,
что добавление в плазму, в качестве
примеси, вещества с низким потенциалом
ионизации (щелочные металлы), степень
ионизации повысится
![]() ,
увеличиться проводимость, а, следовательно,
и ток. Резко снизить проводимость могут
галогены (хлор, фтор), вследсвие того,
что атомы хлора и фтора обладают
способностью захватывать свободные
электроны.
,
увеличиться проводимость, а, следовательно,
и ток. Резко снизить проводимость могут
галогены (хлор, фтор), вследсвие того,
что атомы хлора и фтора обладают
способностью захватывать свободные
электроны.
Перенос под действием градиента концентрации частиц.
В неоднородной плазме плотностью через сечение плазмы S устанавливается диффузионный поток частиц:
![]() ,
где
D
‑
коэффициент диффузии,
,
где
D
‑
коэффициент диффузии,
![]() ,
где V
– ско-рость,
,
где V
– ско-рость,
![]() –
длина свободного
пробега.
–
длина свободного
пробега.
Сила, действующая
на частицу
![]() .
Эта сила уравновешивается силой трения
mvVe
.
.
Эта сила уравновешивается силой трения
mvVe
.
Условие равновесия
имеет вид:
![]() ,
(20)
,
(20)
отсюда
![]() .
Здесь
.
Здесь
![]() ,
а
,
а
![]()
![]() ,
т.к.
,
т.к.
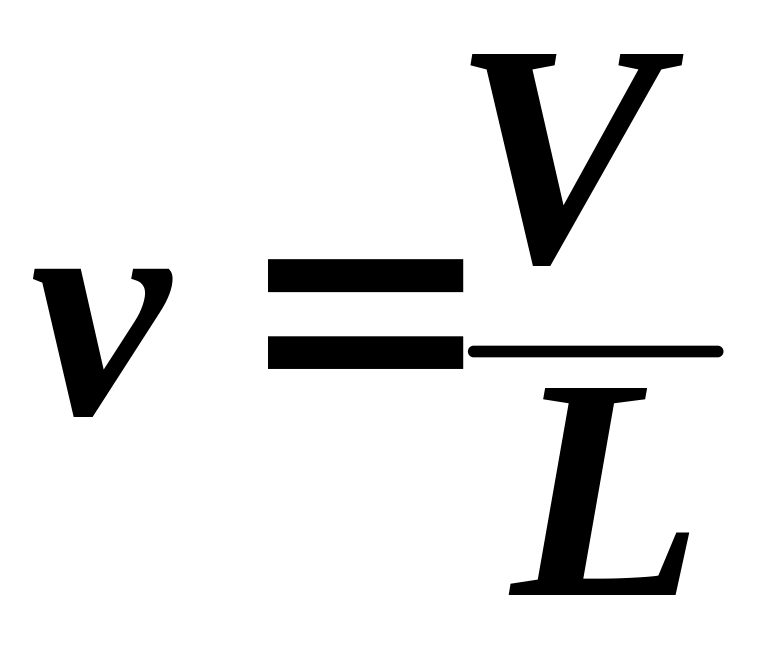 ,
,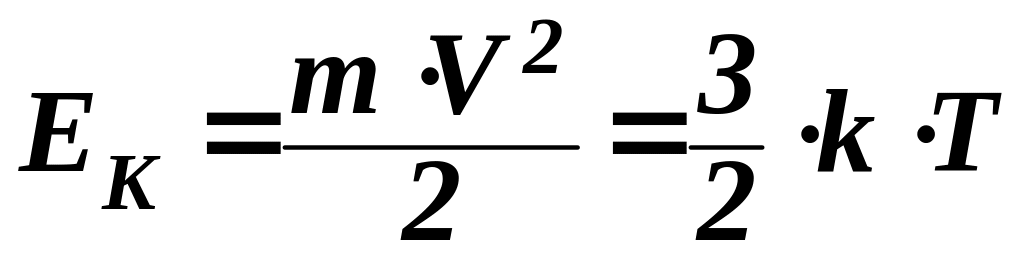 ,
то
,
то
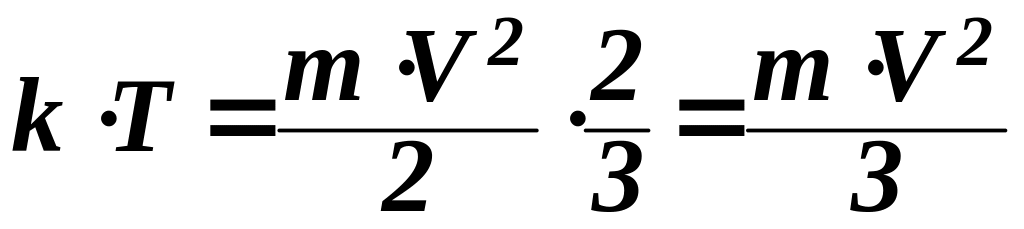 .
.
Подставляя
значение kT
в ( 20), получим
![]() .
.
Коэффициент диффузии в неоднородной плазме зависит от длины свободного пробега частиц, то есть от концентрации частиц.
Эти соотношения
справедливы лишь без учета столкновений
частиц. С повышением концентрации частиц
длина свободного пробега уменьшается
![]() ,
где
,
где
![]() -
характерное сечение столкновения.
Поэтому суммарный направленный поток
частиц равен
-
характерное сечение столкновения.
Поэтому суммарный направленный поток
частиц равен
![]() ,
где
,
где
![]() - разность концентрации частиц на
расстоянии порядка длины свободного
пробега L.
В этом случае коэффициент диффузии
частиц имеет вид:
- разность концентрации частиц на
расстоянии порядка длины свободного
пробега L.
В этом случае коэффициент диффузии
частиц имеет вид:
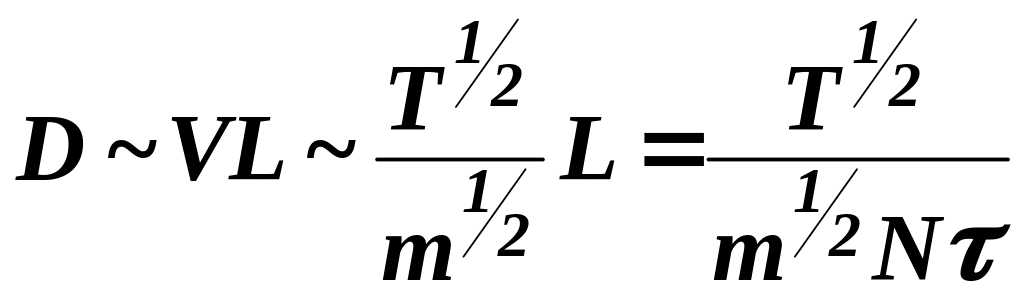 .
.
Характерное
время изменения плотности на расстоянии
![]()
![]()
Время между
столкновениями
![]()
Сравнение этих
времен дает
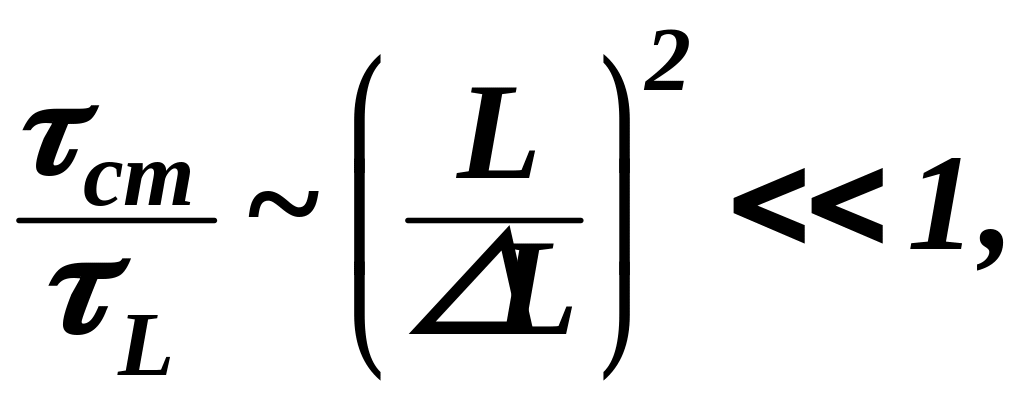 т.е. учет столкновений справедлив, если
концентрация частиц заметно изменяется
на расстоянии
т.е. учет столкновений справедлив, если
концентрация частиц заметно изменяется
на расстоянии
![]() .
.
Перенос под действием градиента температуры
Наличие градиента температуры в плазме вызывает тепловой поток:
![]() (21)
(21)
где f ‑ функция распределения электронов по скоростям.
![]() образующийся
тепловой поток направлен вдоль градиента
температуры
и пропорционален ему:
образующийся
тепловой поток направлен вдоль градиента
температуры
и пропорционален ему:
![]() (22)
(22)
Здесь величина CT называется коэффициентом теплопроводности. Согласно (22) получим тепловой поток:
![]() ,
где T
–
градиент температуры
на расстоянии
,
где T
–
градиент температуры
на расстоянии
![]() ,
то есть равен
,
то есть равен
![]() .
.
Тогда:
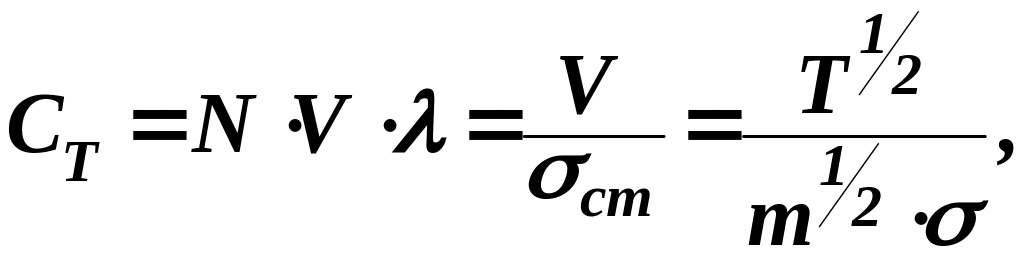 (23)
(23)
где ‑ сечение соударения частиц.
Коэффициент теплопроводности не зависит от концентрации частиц, по той же причине, что и удельная проводимость(слайд 28).
Выше рассмотренные случаи переноса являются переносом частиц. При направленном движении частиц, когда их средняя скорость непостоянна по сечению, возникает перенос импульса mVмежду областями с разными скоростями. Причем частицы с большими скоростями чаще испытывают столкновения – появляется сила трения, тормозящая частицы с высокими скоростями, стремящаяся выровнять среднюю скорость частиц плазмы.
Сила, препятствующая движению частиц (вследствие их взаимного столкновения):
![]() , (24)
, (24)
где
![]()
Коэффициент
![]() носит название коэффициента вязкости
плазмы.
носит название коэффициента вязкости
плазмы.
Сравнивая выражение (24) с (23) получим в конечном итоге:
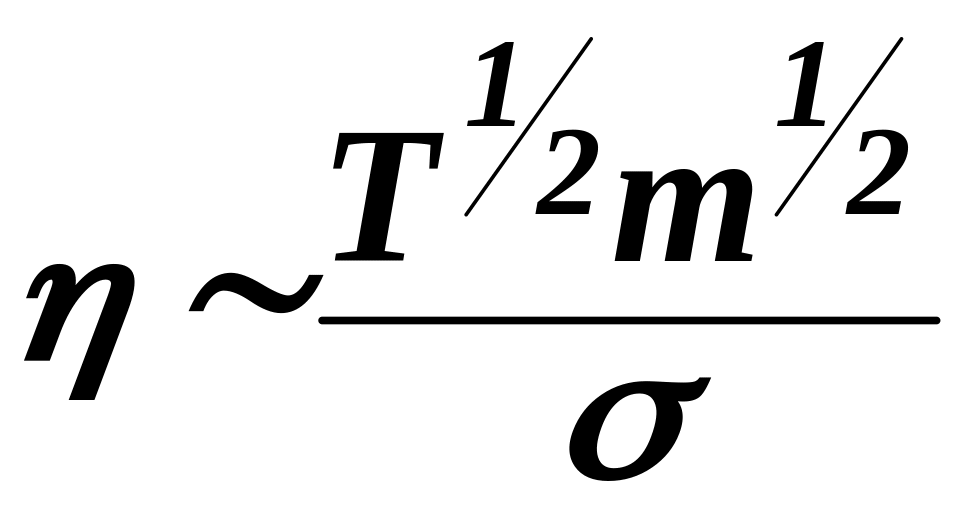
Коэффициент вязкости (как и коэффициент теплопроводности) не зависит от концентрации частиц в плазме. Действительно, с изменением концентрации частицпрямопропорционально изменяется число частиц, участвующих в переносе, но обратнопропорционально изменяется длина свободного пробега частиц. Эти два эффекта взаимно компенсируют друг друга.
- явления переноса имеют место при наличии градиентов макроскопических величин EП, N, T, V
- градиенты потенциала (EП) и плотности (N) вызывают поток частиц, градиент температуры – поток тепла, а градиент средней скорости частиц – поток импульса.
