
- •Тема 7. Теория графов
- •7.1. Основные понятия теория графов
- •7.2. Матричные способы задания графов
- •7.3. Изоморфизм графов
- •7.4. Маршруты и пути
- •7.5. Связность графа
- •7.6. Экстремальные пути в нагруженных ориентированных графах
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из в ( )
- •7.7. Эйлеровы и гамильтоновы графы
- •7.8. Деревья. Основные определения
- •7.9. Минимальные остовные деревья нагруженных графов
- •7.10. Задачи для самостоятельного решения
- •Литература
7.8. Деревья. Основные определения
Неориентированным деревом (или просто деревом) называется связный граф без циклов. Этому определению эквивалентны, следующие определения:
а) дерево есть
связный граф, содержащий
вершин и
![]() ребер;
ребер;
б) дерево есть граф, любые две вершины которого можно соединить простой цепью.
Пример. Графы, изображенные на рис. 34, являются деревьями.

Рис. 34
Если граф несвязный и не имеет циклов, то каждая его связная компонента будет деревом. Такой граф называется лесом.
Остовным деревом связного графа называется любой его подграф, содержащий все вершины графа и являющийся деревом.
Пример. Для графа, изображенного на рис. 35а), графы на рис. 35б) и 35в) являются остовными деревьями.

Рис. 35
Пусть граф
имеет n
вершин и
ребер. Так как всякое дерево с
вершинами по определению имеет
ребер, то любое остовное дерево графа
получается из этого графа в результате
удаления
![]() ребер. Число
ребер. Число
![]() называется цикломатическим
числом
графа.
называется цикломатическим
числом
графа.
7.9. Минимальные остовные деревья нагруженных графов
Пусть – связный нагруженный граф. Задача построения минимального остовного дерева заключается в том, чтобы из множества остовных деревьев найти дерево, у которого сумма длин ребер минимальна.
Приведем типичные случаи, когда возникает необходимость построения минимального остовного дерева графа.
а) Нужно соединить городов железнодорожными линиями (автомобильными дорогами, линиями электропередач, сетью трубопроводов и т.д.) так, чтобы суммарная длина линий или стоимость была бы минимальной.
б) Требуется построить схему электрической сети, в которой клеммы должны быть соединены с помощью проводов наименьшей общей длины.
Задачу построения минимального остовного дерева можно решить с помощью следующего алгоритма Краскала.
Алгоритм Краскала.
Шаг 1.
Установка начальных значений. Вводится
матрица длин ребер
![]() графа
.
графа
.
Шаг 2.
Выбрать в графе
ребро
минимальной длины. Построить граф
![]() ,
состоящий из данного ребра и инцидентных
ему вершин. Положить
,
состоящий из данного ребра и инцидентных
ему вершин. Положить
![]() .
.
Шаг 3.
Если
![]() ,
где
– число
ребер графа, то закончить работу (задача
решена), в противном случае перейти к
шагу 4.
,
где
– число
ребер графа, то закончить работу (задача
решена), в противном случае перейти к
шагу 4.
Шаг 4.
Построить граф
![]() ,
добавляя к графу
,
добавляя к графу
![]() новое ребро
минимальной длины, выбранное среди
всех ребер графа
,
каждое из которых инцидентно какой-нибудь
вершине графа
и одновременно инцидентно какой-нибудь
вершине графа
,
не содержащейся в
.
Вместе с этим
ребром включаем в
и инцидентную
ему вершину, не содержащуюся в
.
Присваиваем
новое ребро
минимальной длины, выбранное среди
всех ребер графа
,
каждое из которых инцидентно какой-нибудь
вершине графа
и одновременно инцидентно какой-нибудь
вершине графа
,
не содержащейся в
.
Вместе с этим
ребром включаем в
и инцидентную
ему вершину, не содержащуюся в
.
Присваиваем
![]() и переходим к шагу 3.
и переходим к шагу 3.
Пример. Найдем минимальное остовное дерево для графа, изображенного на рис. 36.
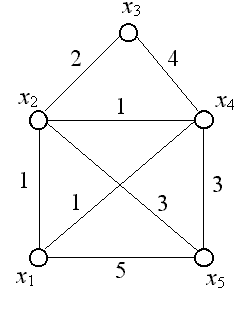
Рис. 36
Шаг 1. Установка начальных значений. Введем матрицу длин ребер :
С = .
.
Шаг 2.
Выберем ребро минимальной длины.
Минимальная длина ребра равна единице.
Таких ребер три:
![]() .
В этом случае можно взять любое. Возьмем
.
В этом случае можно взять любое. Возьмем
![]() .
Построим граф
.
Построим граф
![]() ,
состоящий из данного ребра и инцидентных
ему вершин
,
состоящий из данного ребра и инцидентных
ему вершин
![]() и
и
![]() .
Положим
.
Положим
![]() .
.
Шаг 3.
Так как
![]() ,
то
,
то
![]() ,
поэтому переходим к шагу 4.
,
поэтому переходим к шагу 4.
Шаг 4.
Строим граф
![]() ,
добавляя к графу
новое ребро
минимальной длины, выбранное среди всех
ребер графа
,
каждое из которых инцидентно одной из
вершин
,
и одновременно инцидентно какой-нибудь
вершине графа
,
не содержащейся в
т. е. одной из вершин
,
добавляя к графу
новое ребро
минимальной длины, выбранное среди всех
ребер графа
,
каждое из которых инцидентно одной из
вершин
,
и одновременно инцидентно какой-нибудь
вершине графа
,
не содержащейся в
т. е. одной из вершин
![]() ,
,
![]() ,
,
![]() .
Таким образом, нужно выбрать ребро
минимальной длины из ребер
.
Таким образом, нужно выбрать ребро
минимальной длины из ребер
![]() .
Таких ребер длины единица два:
.
Таких ребер длины единица два:
![]() и
и
![]() .
Можно выбрать любое. Возьмем
.
Вместе с этим ребром включаем в
вершину
,
не содержащуюся в
.
Полагаем
.
Можно выбрать любое. Возьмем
.
Вместе с этим ребром включаем в
вершину
,
не содержащуюся в
.
Полагаем
![]() и переходим к шагу 3.
и переходим к шагу 3.
Шаг 3. Так как , поэтому переходим к шагу 4.
Шаг 4.
Строим граф
![]() ,
добавляя к графу
новое ребро
минимальной длины из ребер
,
добавляя к графу
новое ребро
минимальной длины из ребер
![]() .
Такое ребро длины два одно:
.
Такое ребро длины два одно:
![]() .
Вместе с этим ребром включаем в
вершину
,
не содержащуюся в
.
Полагаем
.
Вместе с этим ребром включаем в
вершину
,
не содержащуюся в
.
Полагаем
![]() и переходим к шагу 3.
и переходим к шагу 3.
Шаг 3. Так как , поэтому переходим к шагу 4.
Шаг 4.
Строим граф
![]() ,
добавляя к графу
новое ребро
минимальной длины из ребер
,
добавляя к графу
новое ребро
минимальной длины из ребер
![]() .
Таких ребер длины три два:
.
Таких ребер длины три два:
![]() и
и
![]() .
Возьмем
.
Вместе с этим ребром включаем в
вершину
,
не содержащуюся в
.
Полагаем
.
Возьмем
.
Вместе с этим ребром включаем в
вершину
,
не содержащуюся в
.
Полагаем
![]() и переходим к шагу 3.
и переходим к шагу 3.
Шаг 3.
Так как
![]() ,
то граф
– искомое минимальное остовное дерево.
Суммарная длина ребер равна
,
то граф
– искомое минимальное остовное дерево.
Суммарная длина ребер равна
![]() .
.
Процесс построения минимального остовного дерева изображен ниже.

