Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе d из в ( )

1. Составляем таблицу , , . Если 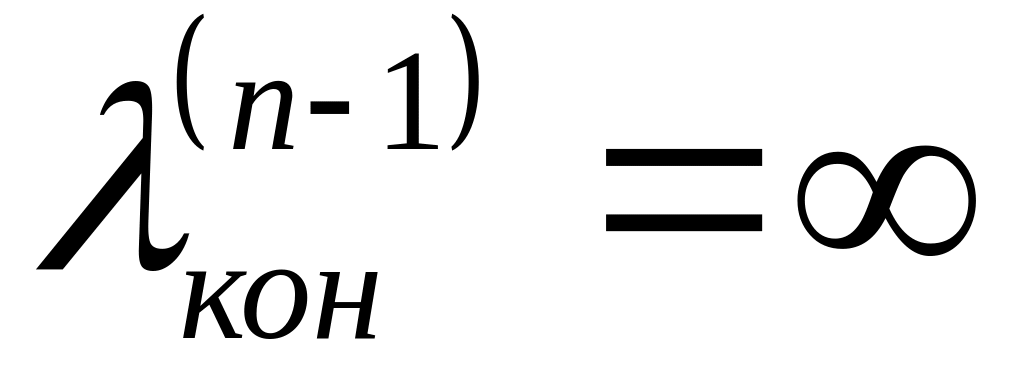, то пути из в нет. Конец алгоритма.

2. Если то это число выражает длину любого минимального пути из в . Найдем минимальное 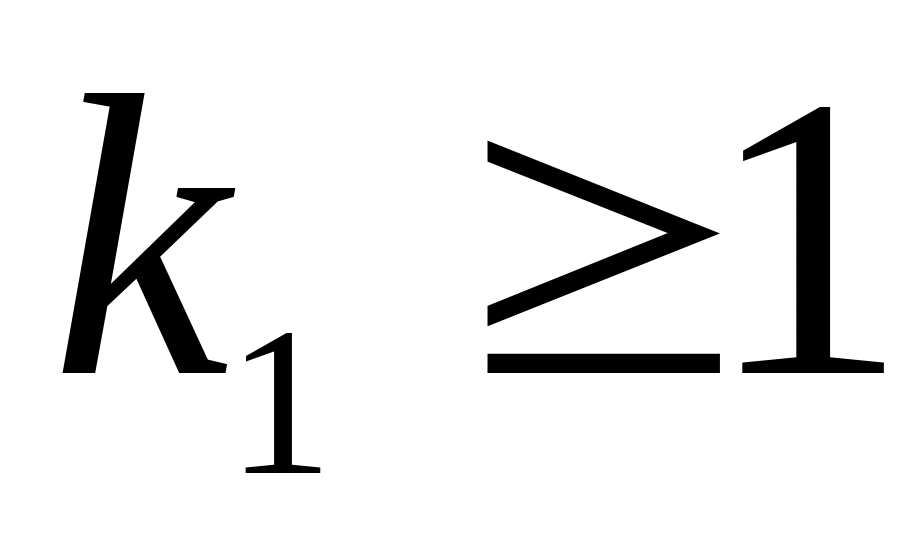, при котором . По определению получим, что 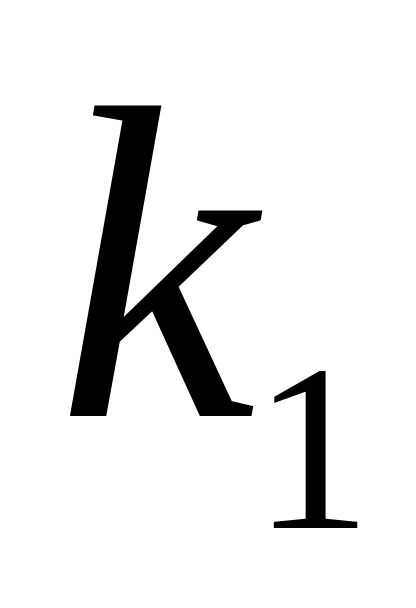 минимальное число дуг в пути среди всех минимальных путей из в .

3. Затем определяем номера 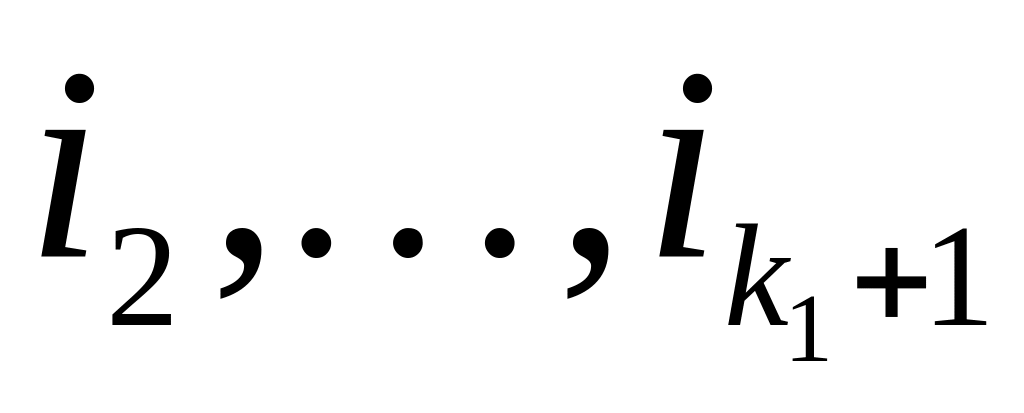такие, что

,

,

,

то есть, восстанавливаем по составленной таблице и матрице стоимости искомый минимальный путь из в .

Пример. Найдем минимальный путь из вершины в в ориентированном нагруженном графе , изображенном на рис. 28. В рассматриваемом графе количество вершин , следовательно, матрица длин дуг ориентированного графа будет иметь размерность .

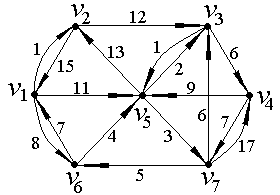
Рис. 28

Матрица длин дуг для рассматриваемого графа будет выглядеть следующим образом:

.

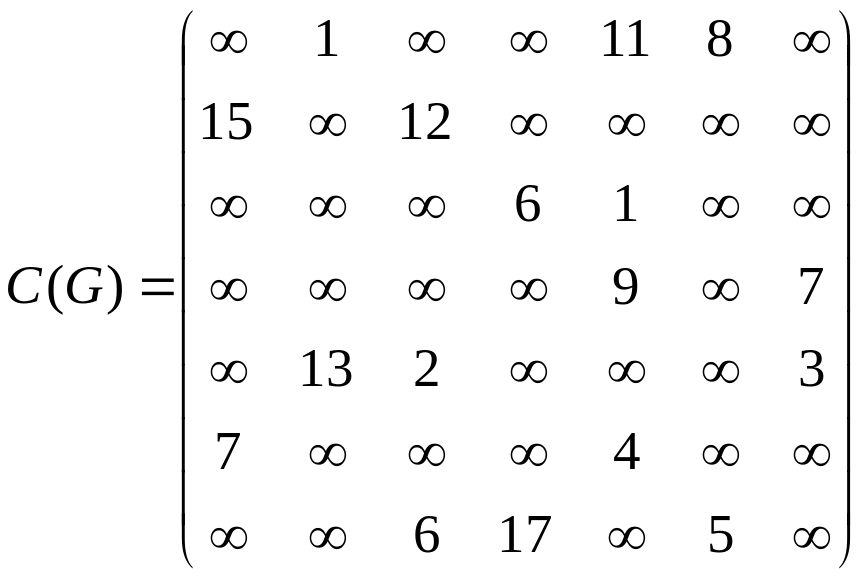Согласно алгоритму, составляем таблицу стоимости минимальных путей из вершины в вершину не более, чем за шагов, ( , следовательно, ). Как было определено выше, , и для всех остальных вершин , то есть первый столбец таблицы состоит из элементов, равных , кроме элемента . Второй столбец таблицы повторяет вторую строку матрицы стоимости, поскольку представляет собой стоимость возможных путей из вершины за один шаг. Далее находим по столбцам все оставшиеся элементы таблицы. Например, чтобы найти элемент , складываем элементы столбца и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел:

.

В конечном итоге получаем следующую таблицу:

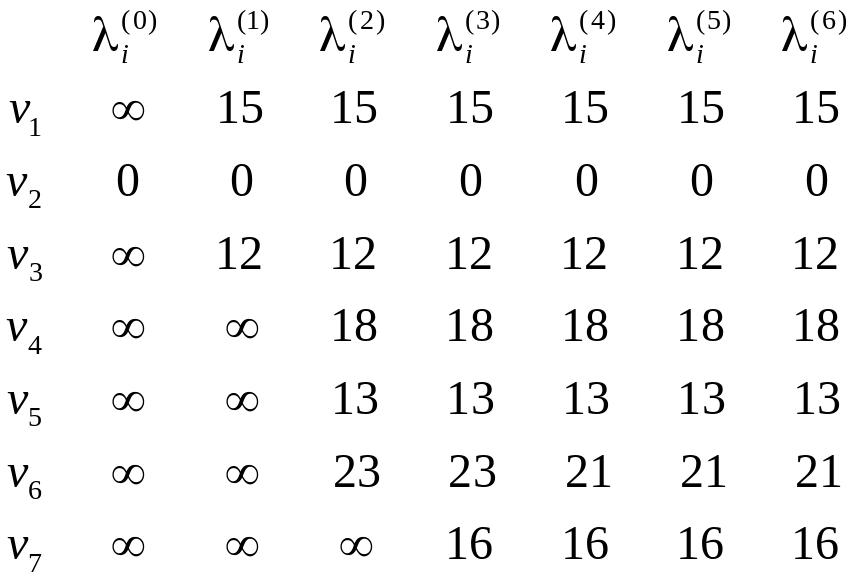
Теперь необходимо по построенной таблице и по матрице восстановить минимальный путь из вершины в , который будет строиться с конца, то есть, начиная с вершины . Для этого выбираем минимальное из чисел, стоящих в строке, соответствующей в таблице. Это число равно 21 и являеися длиной минимального искомого пути. В первый раз такая длина была получена при количестве шагов, равном 4. В вершину можно попасть за один шаг из вершин и (длина соответствующих дуг 8 и 5 соответственно – данные из матрицы ). Выбираем минимальную по длине из этих дуг. Далее, в вершину можно попасть из и (длина соответствующих дуг 7 и 3 соответственно). Продолжая аналогичным образом, найдем искомый путь за 4 шага минимальной длины из вершины в : .

7.7. Эйлеровы и гамильтоновы графы

Определение. Пусть – неориентированный граф. Цикл, который включает все ребра и вершины графа , называется эйлеровым циклом. Граф имеющий эйлеров цикл, называется эйлеровым.

Теорема Эйлера. Конечный граф с более чем одной вершиной имеет эйлеров цикл тогда и только тогда, когда он связанный и каждая его вершина имеет четную степень. Следствие. Связанный граф является эйлеровым тогда и только тогда, когда семейство его ребер можно разбить на непересекающиеся по ребрам циклы.

Определение. Простой связанный граф называется гамильтоновым, если в нем существует цикл, проходящий через все его вершины.

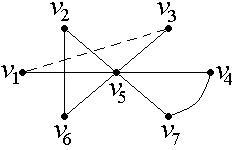
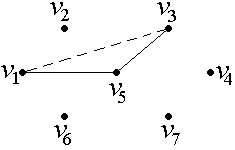
Пример. На рис. 29 графы не являются гамильтоновыми, а граф – гамильтонов граф.

Рис. 29. Гамильтоновы и не гамильтоновы графы

Алгоритм выделения эйлерова цикла в связном мультиграфе с четными степенями вершин:

1. Выделим из цикл 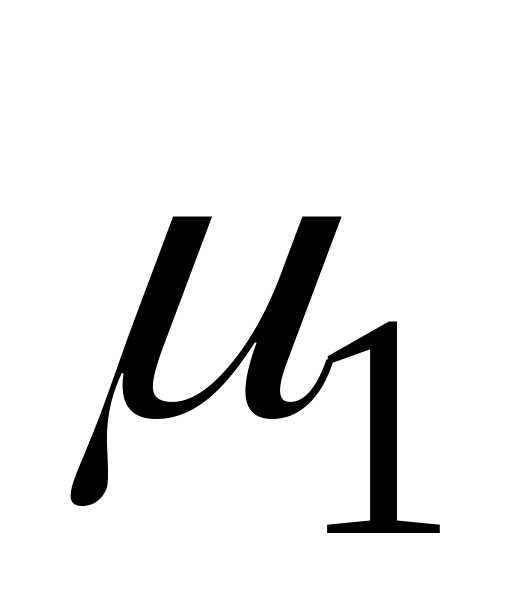(так как степени вершин четны, то висячие вершины отсутствуют). Положим .

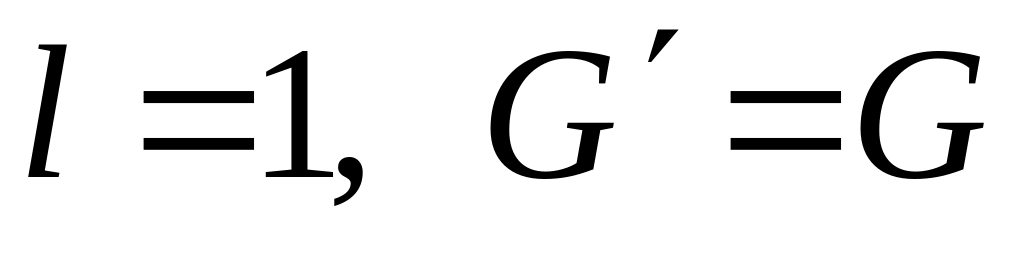2. Удаляем из 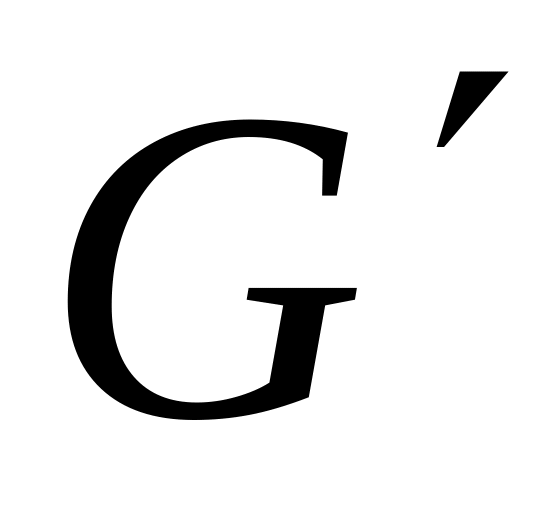ребра, принадлежащие выделенному циклу . Полученный псевдограф снова обозначаем как . Если в отсутствуют ребра, то переходим к шагу 4. Если ребра есть, то выделяем из цикл 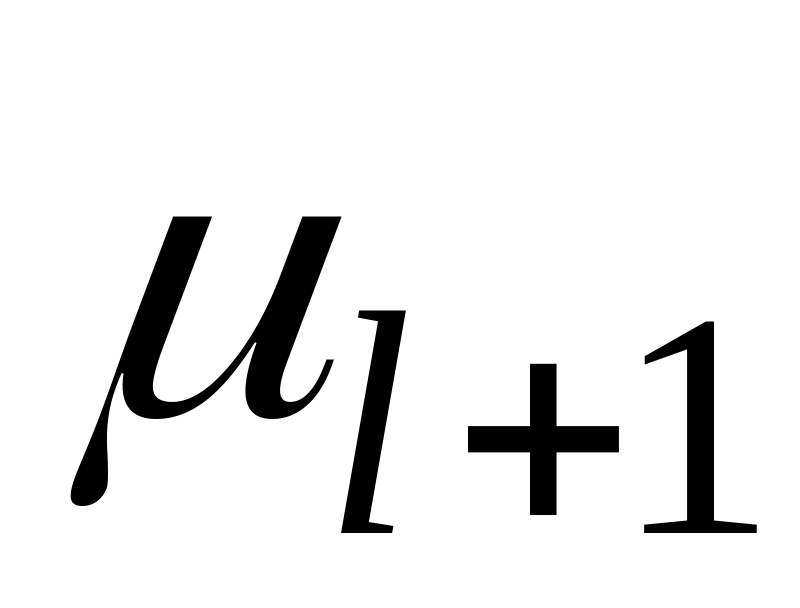и переходим к шагу 3.

3. Присваиваем 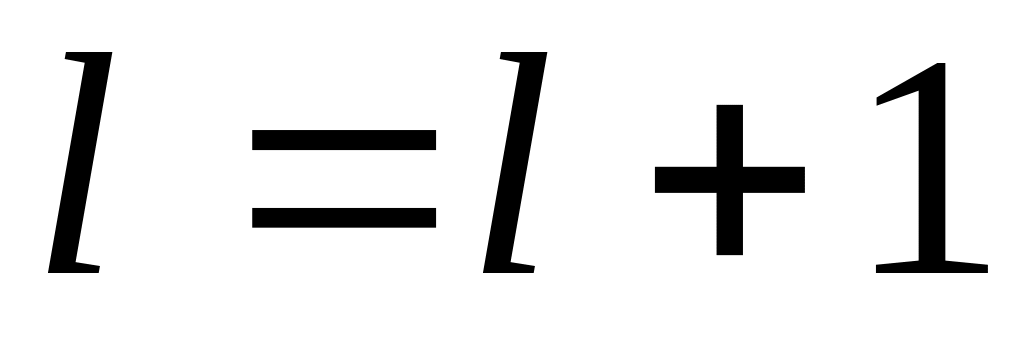и переходим к шагу 2.

4. По построению выделенные циклы содержат все ребра по одному разу. Если 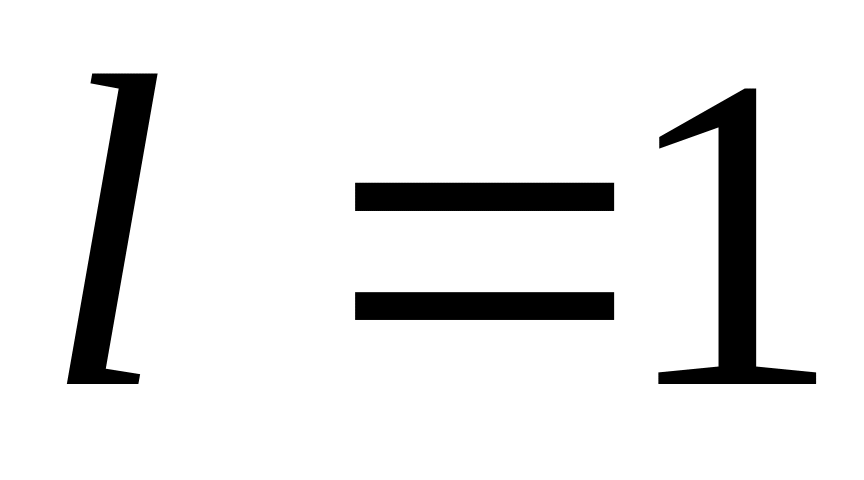, то искомый Эйлеров цикл найден (конец работы алгоритма). В противном случае находим циклы, содержащие хотя бы по одной общей вершине (в силу связности графа это всегда можно сделать). Склеиваем эти циклы. Повторяем эти операции, пока не останется один цикл, который является искомым.

Пример. Найдем эйлерову цепь в неориентированном графе , изображенном на рис. 30. Прежде, чем приступать к нахождению эйлеровой цепи, необходимо проверить степени вершин графа , для существования эйлеровой цепи, необходимо и достаточно, чтобы в графе ровно 2 вершины нечетной степени.

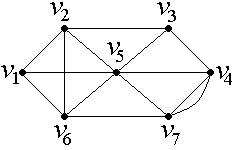
Рис. 30

В рассматриваемом графе нечетные степени имеют вершины и (степень этих вершин равна 3). Соединяя эти вершины фиктивным ребром так, как показано на рис. 31, получаем граф :

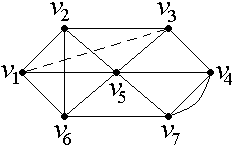
Рис. 31

Поскольку в конечном итоге будет получена цепь, то очевидно, что началом и концом этой цепи будут вершины с нечетными степенями. Поэтому, следуя описанному выше алгоритму, будем циклы так, чтобы хотя бы один из них начинался или кончался на вершинах или .

Пусть цикл составят ребра, проходящие через следующие вершины: . Согласно алгоритму, удаляем из все ребра, задействованные в цикле . Теперь граф будет таким, как показано на рис. 32.

Составляем следующий цикл : . Граф после удаления ребер, составляющих цикл , изображен на рис. 33.

Рис. 32	Рис. 33

Очевидно, что последний цикл будет состоять из , где последнее ребро, соединяющее вершины и – фиктивно. После удаления ребер, составляющих цикл , в графе не останется ни одного ребра.

Теперь по общим вершинам склеиваем полученные циклы. Поскольку и имеют общую вершину , то, объединяя их, получим следующий цикл: . Теперь склеим получившийся цикл с циклом : . Удаляя фиктивное ребро, получаем искомую эйлерову цепь:

.