Контрольная карта Шухарта по альтернативному признаку. P – карта.

Как уже было сказано выше, альтернативные данные не связаны с результатами измерений, представленными в виде числовых значений. Альтернативные данные представляют собой бинарный код, в котором, например, единице сопоставлено состояние годности контролируемого изделия, а нулю – состояние брака.  Такое кодирование  позволяет описывать ситуации, когда контроль производится по качественным признакам без применения измерительных приборов и вывод о состоянии изделия ограничивается выводом  типа годное-брак.  К альтернативному контролю приходим и при контроле изделий, имеющих несколько измеряемых разнотипных параметров качества, когда в конечном счете нас интересует годны ли все измеренные параметры или хотя бы один из них  не укладывается в допуск по техническим условиям и поэтому все изделие следует считать бракованным. И наконец еще один вариант контроля, когда он производится с использованием калибров, что характерно в особенности для механообрабатывающего производства.

Наиболее распространенной картой контроля по альтернативному признаку является  P- карта Шухарта. Алгоритм действия этой карты (ГОСТ Р 50.1.018-98) состоит в следующем. Определяется минимальное число контролируемых объектов  в выборках n (в качестве объекта  может выступать  отдельное изделие или совокупность  изделий, которым в результате контроля сопоставляется вывод  годное-брак). По каждой выборке (подгруппе) находится относительная доля брака  p=m/n, где m – число бракованных  объектов, зарегистрированных в выборке. Эти относительные  доли наносятся на КК и  сравниваются с имеющимися на карте контрольными границами.  Выход  очередной точки за верхнюю контрольную границу означает разладку процесса,  выход   за нижнюю границу КК сигнализирует об улучшении ТП и возможности зафиксировать процесс в этом новом состоянии.

Минимально необходимое число объектов в выборке n находится из условия, что ожидаемое среднее количество бракованных объектов в выборках (подгруппах) должно быть не меньше пяти (ГОСТ Р 50.1.018-98). Отсюда следует

 

                                                                   .                                                                (4.30)

 

Отметим, что выполнение этого условия может привести к необходимости использования весьма значительных  объемов выборок, для построения контрольной карты. Так, при ожидаемой вероятности брака процесса p=0,01  требуемый объем выборки n=500.

            Рассмотрим расчет границ  P-карты Шухарта. Предположим, что вероятность брака анализируемых объектов  известна  (известна точность оборудования, параметров комплектующих и материалов, имеется обширная статистика о случаях брака ТП). Предположим также, что объемы выборок одинаковы. В  этом случае центральная линия КК

 

                                                                 .                                                              (4.31)

 

Для нахождения верхней и нижней границ КК  положим, что число наблюдаемых случаев брака  m укладывается в схему независимых испытаний и  подчиняется биномиальному закону распределения (2.27)

 

                                                 .                                              (4.32)

 

Здесь  обозначает вероятность брака объекта контроля. В  соответствии с биномиальным законом распределения  среднее значение числа бракованных единиц продукции  вычисляется по формуле

 

                                                                  ,                                                               (4.33)

 

дисперсия – по формуле

 

                                                           .                                                        (4.34)

 

С учетом трех последних соотношений найдем среднее значение и дисперсию статистики m/n, используемой  в КК. Очевидно, что

 

                                            .                                         (4.35)

 

 

Из  (4.33) и  (4.34)

 

 

                                                                  ,                                                               (4.36)

 

 

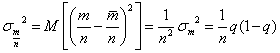                                     .                                  (4.37)

 

Отсюда следуют соотношения для расчета границ КК 

 

                                                    ,                                                 (4.38)

 

 

                                                    .                                                 (4.39)

 

            При неизвестной вероятности брака объектов контроля в выражениях для контрольных границ  (4.31), (4.38), (4.39). следует заменить точные значения вероятностей брака  на их оценки , полученные в результате анализа процесса на заведомо стабильном интервале работы. В остальном вид указанных соотношений остается без изменений. В результате формулы для расчета контрольных границ принимают вид

 

                                                                 ,                                                              (4.40)

 

 

                                                     ,                                                  (4.41)

 

 

                                                     .                                                  (4.42)

 

При выводе соотношений для расчета границ КК предполагалось, что объемы анализируемых выборок (подгрупп) одинаковы. В реальных условиях это не всегда достижимо. В связи с этим в ГОСТ 50779.42-99 приведен алгоритм P – карты, учитывающий, что объемы выборок в подгруппах могут быть разными. В этом случае правила формирования границ КК  (4.38),  (4.39),  (4.41), (4.42)  остаются прежними, но эти границы не остаются постоянными для всей КК, а вычисляются отдельно для каждой выборки (подгруппы). Если объем подгрупп меняется несущественно, то ограничиваются одним набором границ, основанном на среднем объеме подгруппы. Для практических целей достаточно, если объемы подгрупп находятся в пределах от целевого объема подгруппы. Альтернативный вариант для ситуаций, в которых объем группы меняется существенно, - использование нормированных переменных. Например, вместо значений P на карту наносят нормированные значения

 

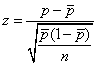                                                                                                                     (4.43)

 

или

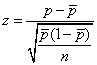                                                            .                                                         (4.44)

 

 

Очевидно, что для этих новых координат центральная линия и контрольные границы остаются постоянными и равными соответственно

 

                                                                  ,                                                               (4.45)

 

 

                                                                 ,                                                              (4.46)

 

 

                                                               .                                                            (4.47)

 

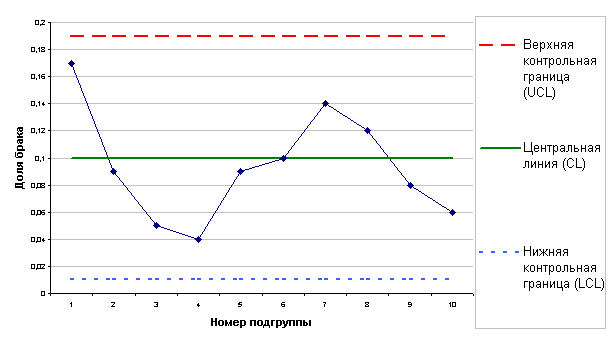
            На рис.4.3 приведен пример выполнения P карты для некоторого процесса, находящегося в статистически устойчивом состоянии.

 

Рисунок 4.3 P- карта Шухарта для альтернативных данных