2.5 Динамическая модель машинного агрегата

В движении входного звена исполнительного рычажного механизма имеют место колебания угловой скорости, основными причинами которых являются:

1) несовпадение законов изменения сил сопротивления и движущих сил в каждый момент времени;

2) непостоянство приведенного момента инерции звеньев исполнительного и некоторых вспомогательных механизмов.

Чтобы учесть влияние названных причин на закон движения входного звена исполнительного механизма, составляется упрощенная динамическая модель машинного агрегата и на ее основе - математическая модель, устанавливающая функциональную взаимосвязь исследуемых параметров.

Наиболее простой динамической моделью машинного агрегата может быть одномассовая модель, представленная на рис. 2.5.1.

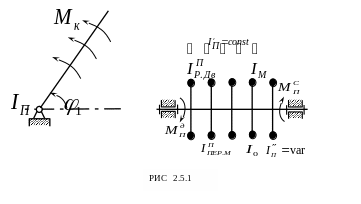
В качестве такой модели рассматривается условное вращающееся звено – звено приведения, которое имеет момент инерции относительно оси вращения (приведенный момент инерции) и находится под действием момента сил (приведенного момента сил). В свою очередь, , где - приведенный момент движущих сил; - приведенный момент сил сопротивления. Кроме того, , где - постоянная составляющая приведенного момента инерции; - переменная составляющая приведенного момента инерции. В величину входят собственный момент инерции кривошипа (I₀), приведенные моменты инерции ротора электродвигателя и передаточного механизма ( ), а также момент инерции I_м добавочной массы (маховика), причем необходимость установки маховика определяется на основании заданной степени неравномерности движения звена приведения.

Динамические характеристики М_П и I_П должны быть такими, чтобы закон вращения звена приведения был таким же, как и у главного вала машины (кривошипа 1 основного исполнительного рычажного механизма), т.е.

2.5.1 Определение приведенного момента движущих сил

Для двигателей приведенный момент сопротивления принимается постоянным ( ), а приведенный момент движущих сил определяется в результате приведения движущих сил и сил тяжести звеньев.

Как отмечено ранее, приведенный момент сил представляется в виде алгебраической суммы

Определение выполняется из условия равенства мгновенных мощностей

.

Откуда

где и - проекции силы на оси координат;

и - проекции аналога скорости точки приложения силы ;

- передаточная функция от -го звена, к которому приложен момент , к звену 1;

= +1 при направлении вращения звена 1 против часовой стрелки;

= -1 при направлении движения звена 1 по часовой стрелке.

В формуле силы , и моменты берутся со знаками, соответствующими правой системе координат (положительное направление движения – против часовой стрелки).

Для горизонтального механизма определяется из равенства

откуда

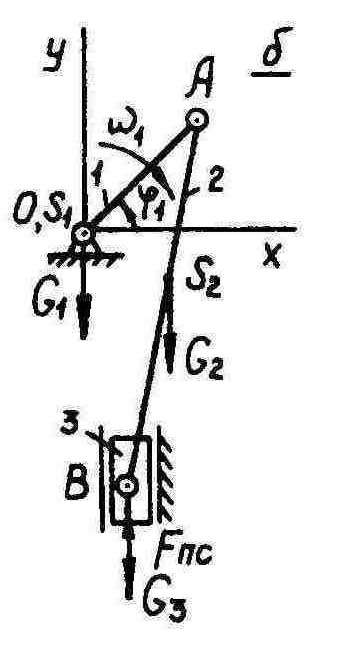
Рис. 2.5.2

Учитывая, что получим

В рассматриваемом положении сила имеет отрицательное значение, так как она направлена против положительного направления оси X.

Рассчитываем значение для второго положения механизма

Разделим на :