
Практическая работа №4.
Тема: Переключательные функции. Способы задания.
Задание №1.
Для f(x,y,z) заданной следующей таблицей истинности удалить несущественную переменную.
Решение:
|
x |
y |
z |
f(x,y,z) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Задание №2
Проверьте двумя
способами, будут ли эквивалентны
следующие формулы:
![]() .
а) составлением таблиц истинности; б) с
помощью эквивалентных преобразований.
.
а) составлением таблиц истинности; б) с
помощью эквивалентных преобразований.
Решение: а) составим сокращенные таблицы истинности обеих формул:
x |
|
(y |
|
z) |
(x |
|
y) |
|
(x |
|
z) |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Поскольку полученные столбцы не совпадают, формулы не эквивалентны.
б)
Преобразуем формулы
к виду СДНФ. Для этого воспользуемся
тождествами:
![]() и
и
![]() ,
где a и b
– произвольные формулы. Тогда
,
где a и b
– произвольные формулы. Тогда
![]()
![]()
![]() (по
закону де Моргана) =
(по
закону де Моргана) =
![]()
![]() (по закону дистрибутивности) =
(по закону дистрибутивности) =
![]() .
.
![]()
![]()
![]()
![]() .
.
Формулы (*) и (**) не совпадают, поэтому исходные формулы не эквивалентны.
Задания для самостоятельного решения
Задание №1
Для f(x,y,z) равной единице на указанных наборах удалить несущественные переменные.
Задание №2
Проверьте двумя способами а) составлением таблиц истинности; б) с помощью эквивалентных преобразований, будут ли эквивалентны формулы.
Варианты заданий:
Вариант №1
f(x,y,z)=(0,5,8,9,10,12,13,15)
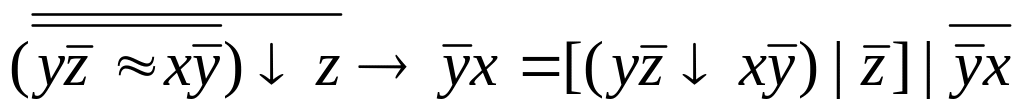
Вариант №2
f(x,y,z)=(0,8,,9,10,12,13,15)
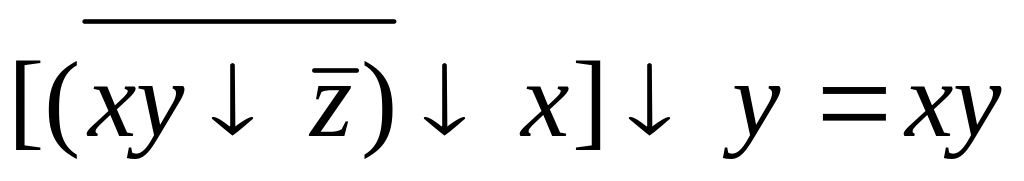
Вариант №3
f(x,y,z)=(1,2,3,12,13,14,15)
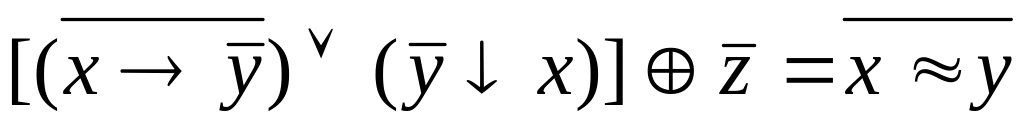
Вариант №4
f(x,y,z)=(2,3,7,8,10,11,12,15)

Вариант №5
f(x,y,z)=(0,4,6,7,8,10,13,15)
Вариант №6
f(x,y,z)=(0,4,5,7,8,10,11,13,15)
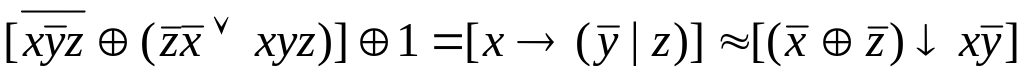
Вариант №7
f(x,y,z)=(0,4,5,6,7,14,15)
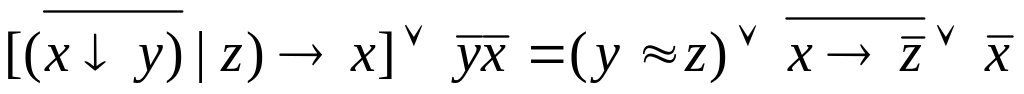
Вариант №8
f(x,y,z)=(2,4,7,9,10,14,15)
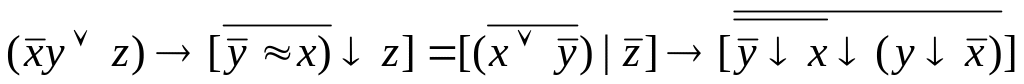
Вариант №9
f(x,y,z)(0,3,7,8,9,10,11,12,15)
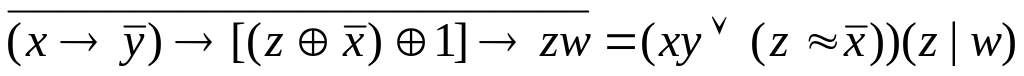
Вариант №10
f(x,y,z)=(0,2,4,7,8,10,13,15)
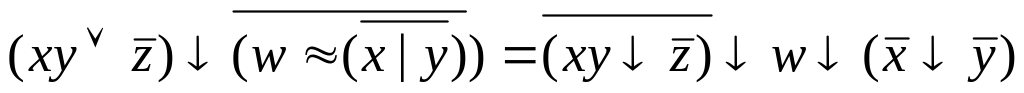
Вариант №11
f(x,y,z)=(0,2,4,7,8,10,13,15)
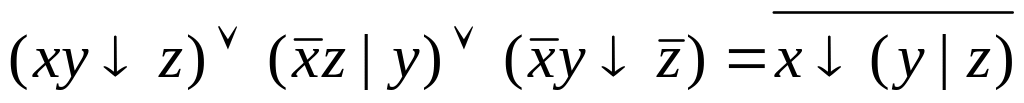
Вариант №12
f(x,y,z)=0,3,6,8,9,12,13,15)
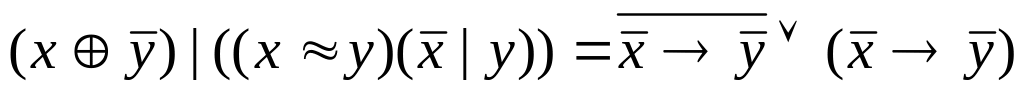
Вариант №13
f(x,y,z)=(2,4,7,9,10,11,13,15)
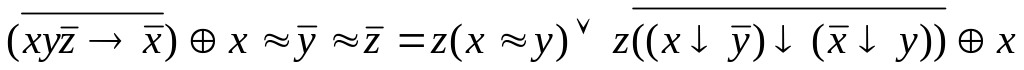
Вариант №14
f(x,y,z)=(2,3,4,5,9,10,11,15)
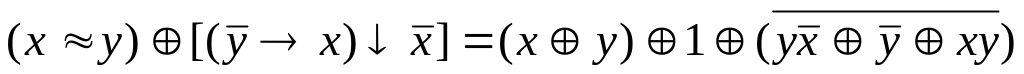
Вариант №15
f(x,y,z)=(5,7,8,9,10,11,15)
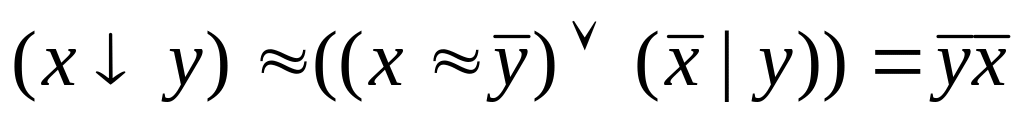
Вариант №16
f(x,y,z)=(2,3,4,9,10,11,14,15)
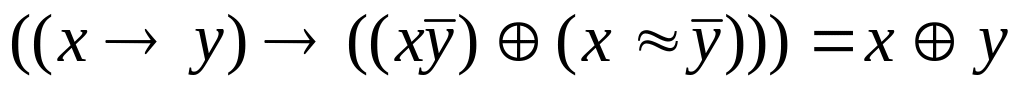
Вариант №17
f(x,y,z)=(0,2,4,8,12,14,15)
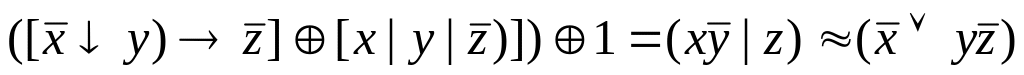
Вариант №18
f(x,y,z)=(2,3,4,6,8,9,11,12)
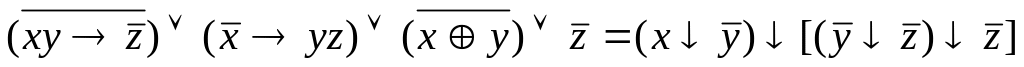
Вариант №19
f(x,y,z)=(5,6,7,8,9,10,11,12,13)
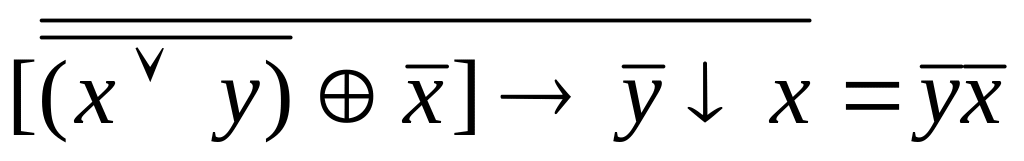
Вариант №20
f(x,y,z)=(3,5,7,10,11,12,13,14)
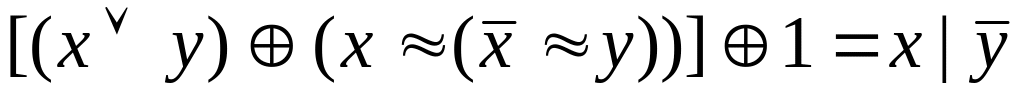
Практическая работа №5.
Тема: Специальные разложения ПФ.
Задание №1.
Для функции, заданной своими истинностными значениями, запишите: СДНФ, СКНФ и СПНФ.
f(x, y, z) = ( 1, 0, 1, 0, 0, 1, 1, 0 )
Решение: СКНФ
строится по нулевым наборам, СДНФ – по
единичным наборам, а СПНФ может быть
получена из СДНФ путем замены «»
на «» и «![]() »
на «x1».
См. таблицу .
»
на «x1».
См. таблицу .
Таблица
x |
y |
z |
f(x,y,z) |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
СКНФ(f(x,y,z))=![]() .
.
СДНФ(f(x,y,z))=![]() .
.
Используем тождество: aa=0.
СПНФ(f(x,y,z))=(x1)(y1)(z1) (x1)y(z1) x(y1)z xy(z1)= (xyzxyxzxyzyz1) (xyzxyyzy) (xyzxz) (xyzxy) = xzzx1.
Задание №2
С помощью эквивалентных преобразований приведите формулу к виду ДНФ, КНФ, СДНФ, СКНФ.
![]()
Решение:
используем тождества:
![]()
![]()
Для компактности записи вместо «a&b» , будем писать «ab».
ДНФ=![]()
![]()
![]()
![]()
КНФ=![]()
Совершенную
дизъюнктивную нормальную форму (СДНФ)
получим из ДНФ. Для этого к первой
элементарной конъюнкции добавим
единичный множитель
![]() ,
а ко второй –
,
а ко второй –![]() .
.
СДНФ=![]()
Совершенную
конъюнктивную нормальную форму (СКНФ)
получим из КНФ. Для этого к первой
элементарной дизъюнкции добавим нулевое
слагаемое
![]() ,
а ко второй –
,
а ко второй –
![]() .
.
СКНФ=![]()
СПНФ=xyz xy(z1) (x1)yz (x1)(y1)z x(y1)z = xyz xyz xy xyz yz xyz xz yz z xyz xz = xyzxyz
Задания для самостоятельного выполнения:
Задание №1
Для функции, заданной своими истинностными значениями, запишите: СДНФ, СКНФ и СПНФ.
Задание №2
С помощью эквивалентных преобразований приведите формулу к виду ДНФ, КНФ, СДНФ, СКНФ.
Варианты заданий:
Вариант №1
1. f(x,y,z)=(0,1,2,6,7,8,12,13,14)
2.
![]()
Вариант №2
1. f(x,y,z)=(4,6,8,9,11,12)
2.
![]()
Вариант №3
1. f(x,y,z)=(0,1,2,3,6,12)
2.![]()
Вариант №4
1. f(x,y,z)=(0,6,10,14)
2.![]()
Вариант №5
f(x,y,z)=(3,4,7)
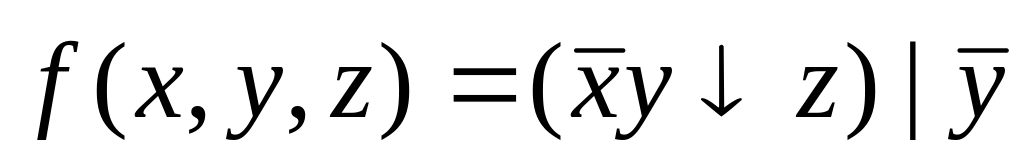
Вариант №6
f(x,y,z)=(0, 1, 2, 3, 4)
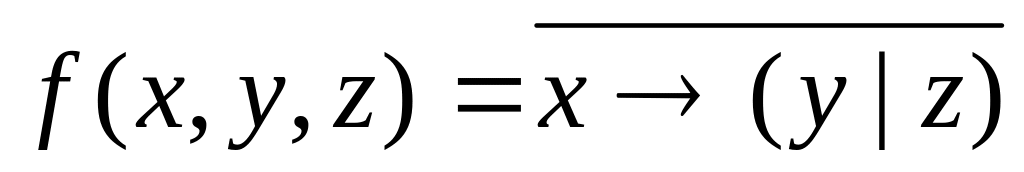
Вариант №7
f(x,y,z)=(1, 2, 5, ,7)
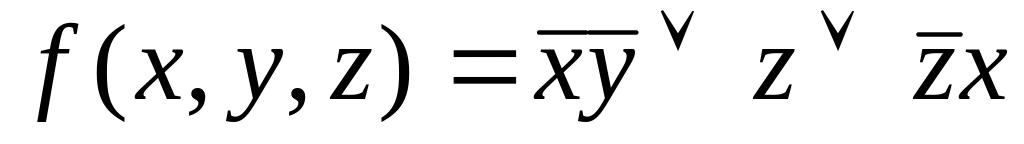
Вариант №8
f(x,y,z)=(1, 2, 4)
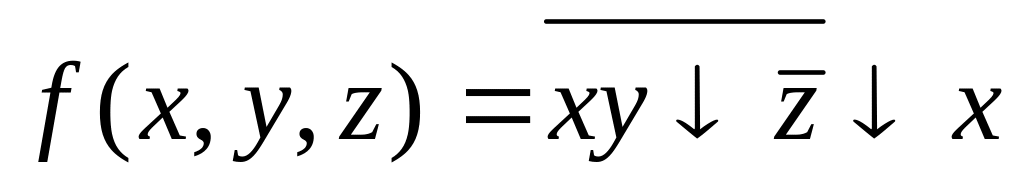
Вариант №9
f(x,y,z)=(0, 1, 2, 3, 4, 5, 6)
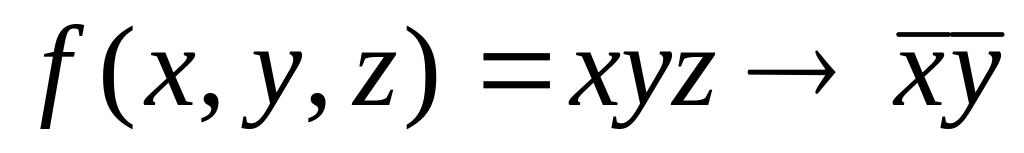
Вариант №10
f(x,y,z)=(1, 2, 3, 4, 5, 6)
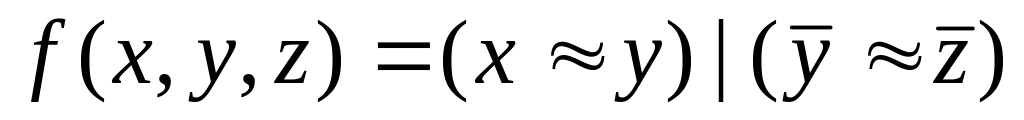
Вариант №11
f(x,y,z)=(2, 3, 4, 5)
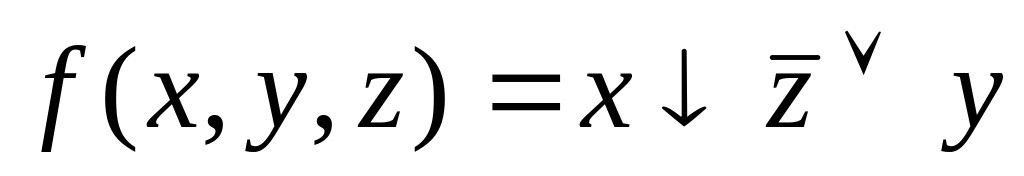
Вариант №12
f(x,y,z)=(0, 2, 3, 4, 7)
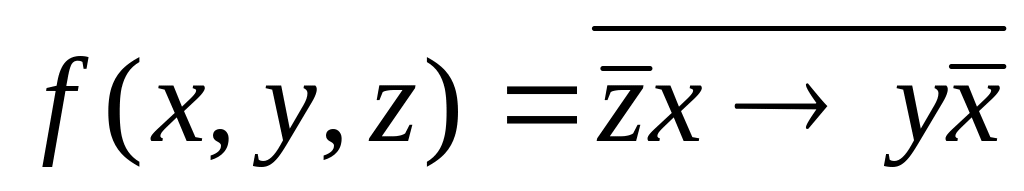
Вариант №13
f(x,y,z)=(0, 3, 4, 6, 7)
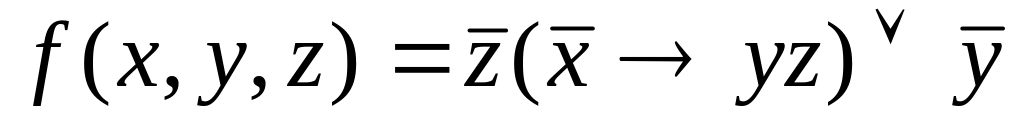
Вариант №14
f(x,y,z)=(1, 2, 3, 7)
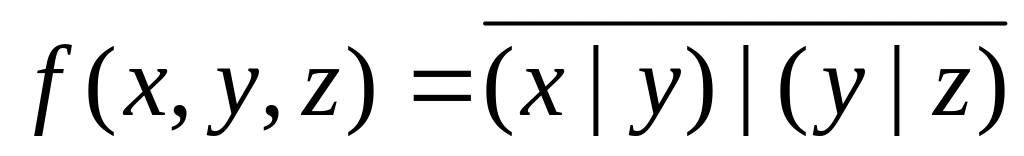
Вариант №15
f(x,y,z)=(0, 1, 2, 5)
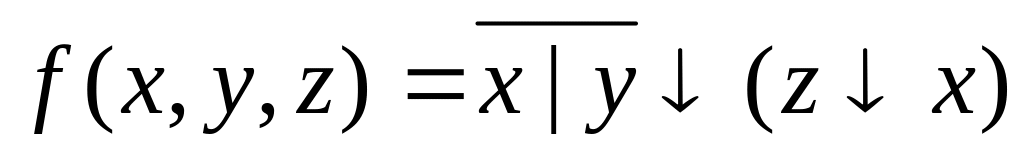
Вариант №16
f(x,y,z)=(1, 2, 4, 5)
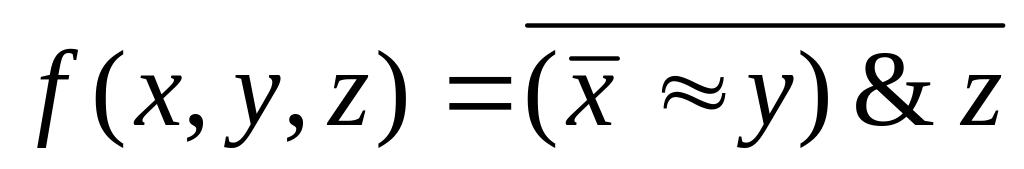
Вариант №17
f(x,y,z)=(0, 3, 4, 7)
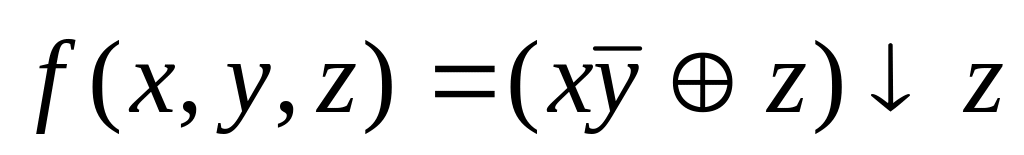
Вариант №18
f(x,y,z)=(1, 2, 4, 5, 6)
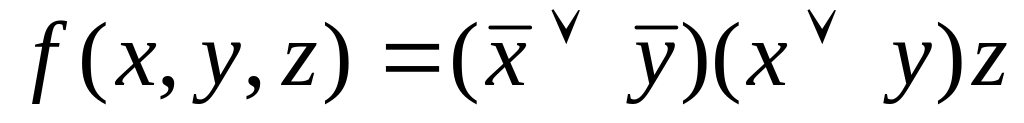
Вариант №19
f(x,y,z)=(1,2, 3, 6)
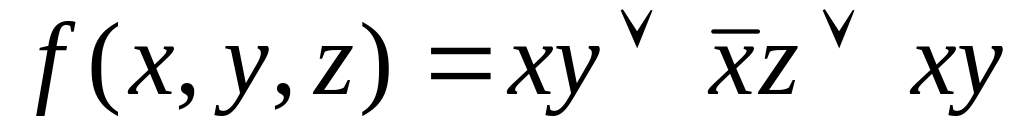
Вариант №20
f(x,y,z)=(0, 1, 3, 4, 6, 7)
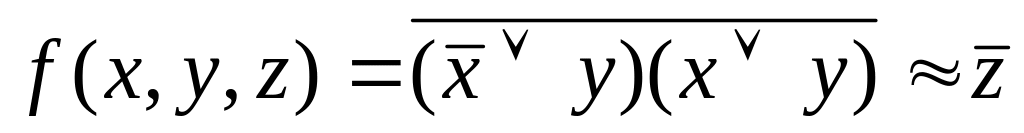
Практическая работа №6.
Тема: Теорема о функциональной полноте.
Задание №1.
Определите к каким классам относится функция следующего вида:
![]() (0,
1, 1, 0, 0, 1, 1, 1)
(0,
1, 1, 0, 0, 1, 1, 1)
x |
y |
z |
f(x,y,z) |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Запишем значения функции в таблицу истинности.
Т.к. f(0,0,0)=1, то f T0 (класс функций, сохраняющих ноль).
Т.к. f(1,1,1)=1, то f T1 (класс функций, сохраняющих единицу).
Т.к. f*(x,y,z)=(0, 0, 0, 1, 1, 0, 0, 1)f(x,y,z), то fS (класс самодвойственных функций).
Рассмотрим наборы: (0,0,1) и (0,1,1). Заметим, что f() =1, f() =0.
Т.к. , но f()f(), то f M (класс монотонных функций).
Найдем полином Жегалкина (СПНФ):
f(x,y,z)= xyz y x.
Т.к. в СПНФ имеются нелинейные слагаемые, то f L (класс линейных функций).
Задание №2
Определите, является ли полной система функций? Образует ли она базис?
F={![]() }.
}.
Решение: построим таблицы истинности для функций системы F .
x |
y |
|
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
СПНФ (
)
=
![]()
Оформим в виде принадлежность функций из F классам Поста:
|
T0 |
T1 |
S |
M |
L |
|
– |
– |
– |
– |
– |
|
- |
– |
+ |
– |
+ |
Задания для самостоятельного выполнения:
Задание №1.
Определите к каким классам относится функция следующего вида:
Задание №2
Определите, является ли полной система функций? Образует ли она базис?
Варианты заданий:
Вариант №1
f(x,y,z)=(7, 8, 9, 10, 12, 15)
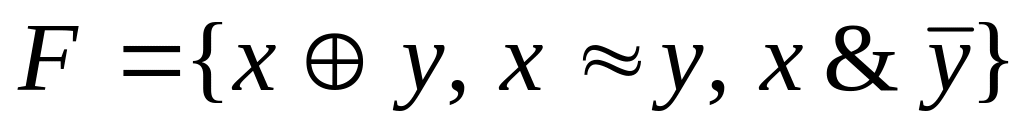
Вариант №2
f(x,y,z)=(7, 9, 11, 12, 14)
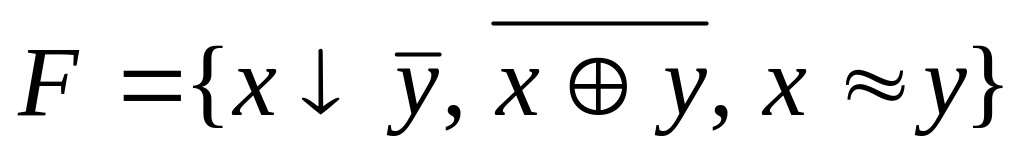
Вариант №3
f(x,y,z)=(1, 3, 5, 7, 8, 9, 11, 12, 14)
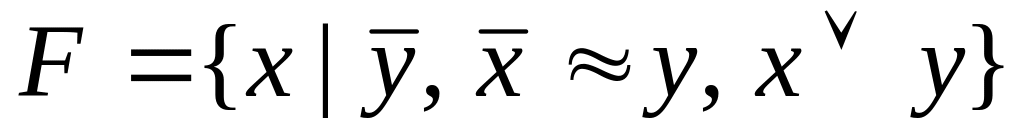
Вариант №4
f(x,y,z)=(7, 8, 9, 10, 11, 12, 15)
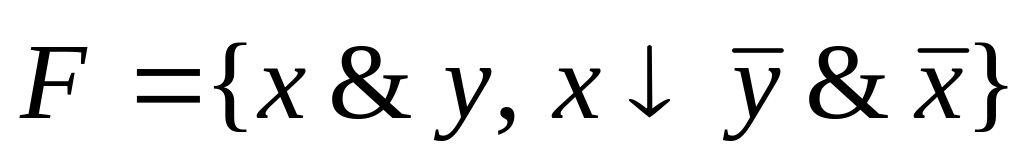
Вариант №5
f(x,y,z)=(7, 8, 9, 10, 12, 15)
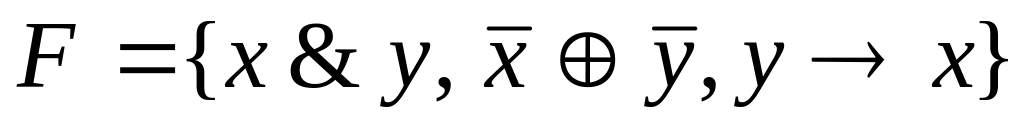
Вариант №6
f(x,y,z)=(0,4, 8, 9, 10, 14)
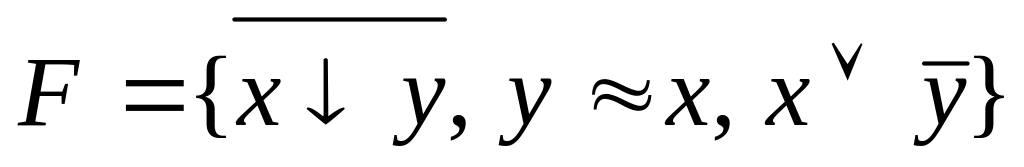
Вариант №7
f(x,y,z)=(1, 2, 7, 8, 12, 15)
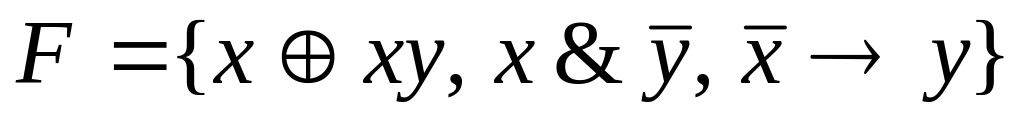
Вариант №8
f(x,y,z)=(2, 3, 4, 5, 7, 8, 12, 15)
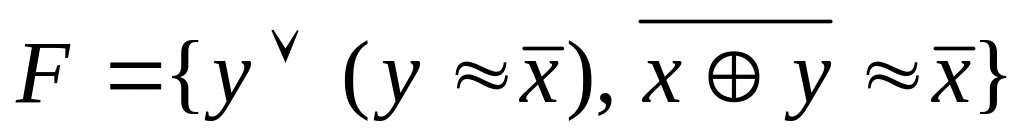
Вариант №9
f(x,y,z)=(0, 1, 3, 5, 7, 9, 11)
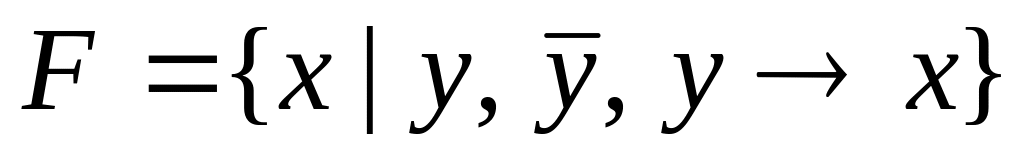
Вариант №10
f(x,y,z)=(4, 6, 8, 10, 12, 14)
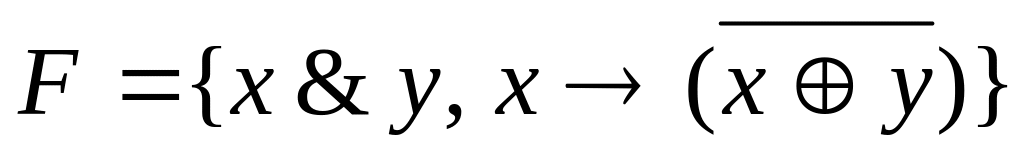
Вариант №11
f(x,y,z)=(3, 5, 7, 8, 11, 13, 14)
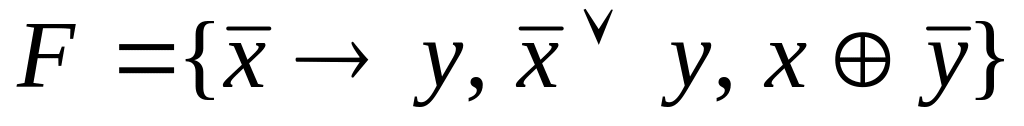
Вариант №12
f(x,y,z)=(3, 5, 6, 7, 9, 12, 13, 15)
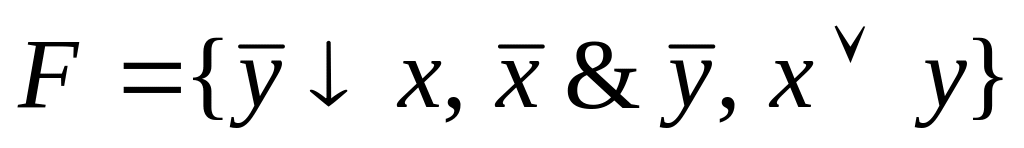
Вариант №13
f(x,y,z)=(4, 7, 8, 9, 11, 12, 15)
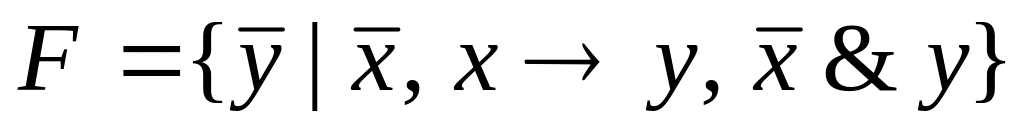
Вариант №14
f(x,y,z)=(2, 6, 8, 9, 10, 11, 12, 13, 14)
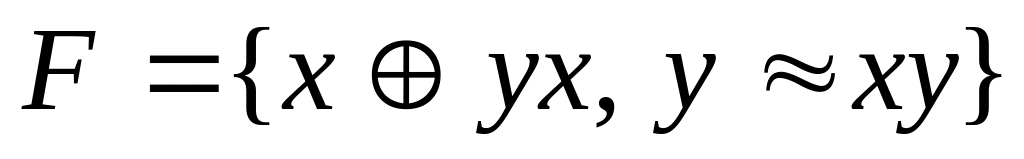
Вариант №15
f(x,y,z)=(0, 2, 3, 4, 5, 8, 9)
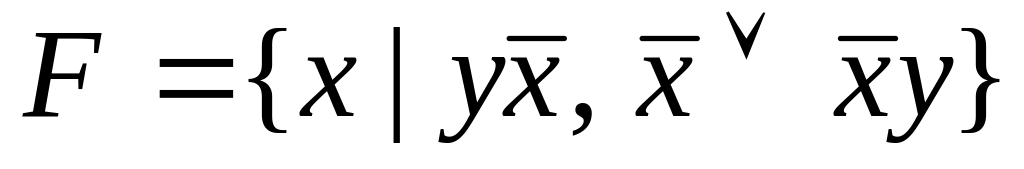
Вариант №16
f(x,y,z)=(3, 4, 5, 6, 7, 8, 9, 10, 12, 13)
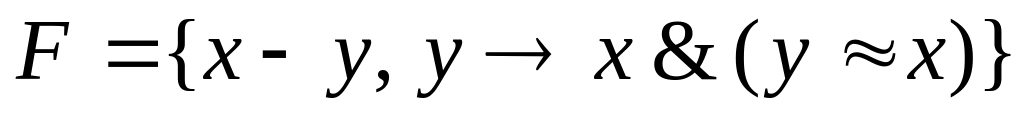
Вариант №17
f(x,y,z)=(0, 1, 2, 3, 4, 10, 11, 12, 15)
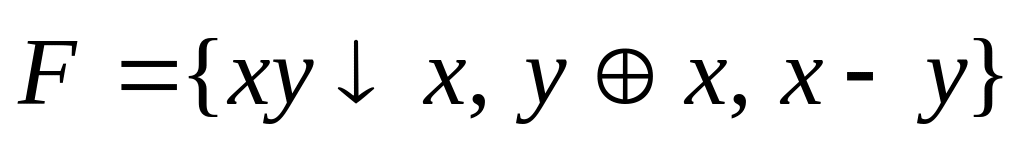
Вариант №18
f(x,y,z)=(0,3,7,8,11,13,14,15)

Вариант №19
f(x,y,z)=(0, 2, 4, 5, 6, 8, 10, 11)
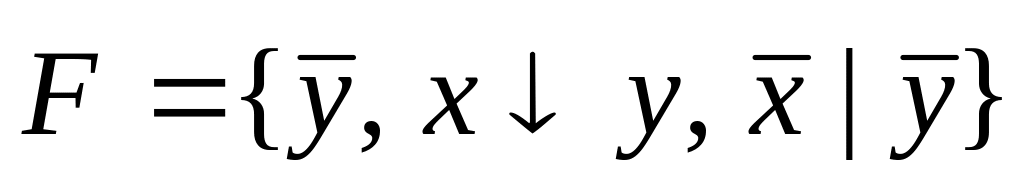
Вариант №20
f(x,y,z)=(5, 6, 8, 9, 12, 13, 14, 15)
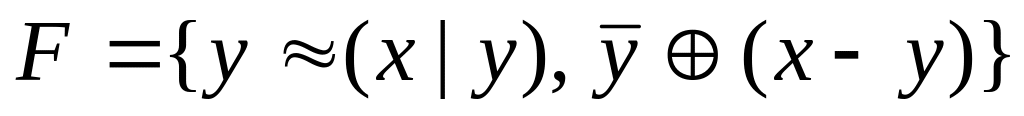
Практическая работа №7
Тема: Минимизация ПФ и не полностью определённых ПФ.
Задание №1
Пусть дана функция от трех переменных f(x, y, z)=(0,1,1,1,1,1.1,0). Найти её МДНФ методом неопределённых коэффициентов.
Решение:
Построим таблицу истинности для данной функции. Она будет иметь следующий вид:
x |
y |
z |
f(x,y,z) |
|
0 |
0 |
0 |
0 |
В ДНФ общего вида такой функции будет |
0 |
0 |
1 |
1 |
26 неопределенных коэффициентов. Для обо‑ |
0 |
1 |
0 |
1 |
значения этих коэффициентов будем |
0 |
1 |
1 |
1 |
использовать букву К с нижним индексом, |
1 |
0 |
0 |
1 |
указывающим конъюнкцию, перед которой |
1 |
0 |
1 |
1 |
стоит этот коэффициент. С учетом всех |
1 |
1 |
0 |
1 |
принятых обозначений ДНФ общего вида |
1 |
1 |
1 |
0 |
запишется так: |
ДНФ = k
 kx x k
kx x k ky y k
ky y k kz z k
k
y
y
kx
x
kx y x y k
kz z k
k
y
y
kx
x
kx y x y k
 k
z
z kx
x
kx z x z
k
k
z
z ky
y
ky z y z k
k
z
z
k
y
y
k
y z
y z kx
x
kx
z x
z kx y
x y
kx y z x y z
k
z
z kx
x
kx z x z
k
k
z
z ky
y
ky z y z k
k
z
z
k
y
y
k
y z
y z kx
x
kx
z x
z kx y
x y
kx y z x y zТеперь последовательно подставляя в ДНФ каждый набор значений переменных и приравнивая при этом получаемые выражения к значению функции на этом наборе, получим следующую систему уравнений: ДНФ(0,0,0): k k k k k k k =0; ДНФ(0,0,1): k k kz k k z k z k z =1; ДНФ(0,1,0): k ky k k y k ky k y =1; ДНФ(0,1,1): k ky kz k y k z ky z k y z =1; ДНФ(1,0,0): kx k k kx kx k kx =1; ДНФ(1,0,1): kx k kz kx kx z k z kx z =1; ДНФ(1,1,0): kx ky k kx y kx ky kx y =1; ДНФ(1,1,1): kx ky kz kx y kx z ky z kx y z =0;
Выполним шаг 3, приравнивая все коэффициенты первого и последнего уравнений к нулю.
Вычеркнув все нулевые коэффициенты, получим новую систему уравнений, в которой число неизвестных меньше, чем в исходной, но все же превышает число самих уравнений: k z k z k z =1; k y ky k y =1; k y k z k y z =1; kx kx kx =1; kx k z kx z =1; kx ky kx y =1;
В каждом уравнении полученной системы имеется по два коэффициента, которые могут быть приравнены к 1. Отсюда вытекает неоднозначность решения задачи. Учитывая то, что в каждом уравнении следует выбрать лишь один коэффициент, получим следующие два решения:
Первое: k z =1; ky =1; kx =1;
Второе: k z =1; k y =1; kx =1;
Остальные коэффициенты в обоих случаях приравниваем к нулю.
Подставляя найденные коэффициенты в исходную ДНФ, получим две минимальных ДНФ для заданной функции:
МДНФ1 = z y x ; и
МДНФ2 = z y x ;
Задание№2
Пусть функция от трех переменных f(x, y, z) задана в виде f(x,y,z)=(1,0,0,0,1,0,1,1). Построить её СокрДНФ.
Решение:
Для нахождения СокрДНФ необходимо построить СДНФ. Для данной функции СДНФ будет иметь вид: f(x, y, z) = x x y x y z
Используя законы склеивания ( x A B = x A B AB - склеивание; или x A A = A - полное склеивание или x A A = x A A A - неполное склеивание)
выполним всевозможные склеивания, т.е. будем склеивать первую конъюнкцию со второй, третьей, четвертой, затем вторую с третьей и четвертой, и наконец, третью с четвертой.
Тогда f(x, y, z) = x x y x y z y
y z x x x z x y = x x y x y z
x x y
Теперь выполняя всевозможные поглощения (A AB = A - поглощение, где A и B - элементарные конъюнкции), получим:
f(x, y, z) = x x y
Поскольку преобразования больше невозможны, последняя формула является СокрДНФ.
Задания для самостоятельного решения:
Задание №1
Пусть дана функция от трех переменных f(x, y, z). Найти её МДНФ методом неопределённых коэффициентов.
Задание№2
Пусть дана функция от четырёх переменных f(x, y, z, w). Построить её СокрДНФ.
Варианты заданий:
Вариант №1
f(x,y,z)=(2,3,5,6)
f(x,y,z)=(3,6,7,8,10,11,14)
Вариант №2
f(x,y,z)=(1,2,3,7)
f(x,y,z)=(2,3,4,5,10,12,13,15)
Вариант №3
f(x,y,z)=(0,3,4,5)
f(x,y,z)=(6,7,8,10,11,13)
Вариант №4
f(x,y,z)=(5,6,7)
f(x,y,z)=(2,4,6,9,10,11,12,13)
Вариант №5
f(x,y,z)=(1,2,4,5,6,7)
f(x,y,z)=(2,4,5,6,8,11,12,14)
Вариант №6
f(x,y,z)=(0,2,3,5,7)
f(x,y,z)=(2,3,5,6,7,8,10,12,14)
Вариант №7
f(x,y,z)=(0,3,5,7)
f(x,y,z)=(2,3,4,5,12,13,14)
Вариант №8
f(x,y,z)=(0,1,2,3)
f(x,y,z)=(1,2,5,7,8,12,13,14)
Вариант №9
f(x,y,z)=(1,2,4,6,7)
f(x,y,z)=(1,5,6,7,8,9,10,15)
Вариант №10
f(x,y,z)=(0,1,2,3,4)
f(x,y,z)=(2,3,9,10,13,14,15)
Вариант №11
f(x,y,z)=(1,3,4,6)
f(x,y,z)=(0,2,5,6,8,11,12,13)
Вариант №12
f(x,y,z)=(2,4,5,7)
f(x,y,z)=(1,4,6,7,10,11,12,14)
Вариант №13
f(x,y,z)=(1,2,3,6)
f(x,y,z)=(0,2,5,7,8,9,11,12)
Вариант №14
f(x,y,z)=(0,1,2,3,4)
f(x,y,z)=(1,2,5,7,8,9,10,11,15)
Вариант №15
f(x,y,z)=(0,1,2,6)
f(x,y,z)=(3,5,6,7,8,9,13,14)
Вариант №16
f(x,y,z)=(2,3,6,7)
f(x,y,z)=(0,1,2,7,8,9,10,13,14)
Вариант №17
f(x,y,z)=(3,4,5,6)
f(x,y,z)=(2,6,7,10,12,14,15)
Вариант №18
f(x,y,z)=(3,4,6,7)
f(x,y,z)=(1,2,4,5,8,9,11,12)
Вариант №19
f(x,y,z)=(3,5,6,7)
f(x,y,z)=(3,4,5,6,8,9,10,11)
Вариант №20
f(x,y,z)=(0,5,6,7)
f(x,y,z)=(1,3,5,8,9,10,11,12)
Практическая работа №8
Тема: Минимизация ПФ и не полностью определённых ПФ методами, основанными на геометрическом представлении функций алгебры логики
Задание№1
Пусть функция имеет следующие значения: f(x, y, z)=(1, 0, 0, 1, 1, 0,1, 1). Найти МДНФ функции методом Куайна.
Решение:
Для
данной функции запишем её СДНФ:
![]() .
.
Построим СокрДНФ:
![]()
|
|
|
|
|
xyz |
|
1 |
|
1 |
|
|
yz |
|
1 |
|
|
1 |
|
|
|
1 |
1 |
|
xy |
|
|
|
1 |
1 |
Задание №2
Для функции заданной следующим образом f(x,y,z,w)=(1,1,1,1,0,1,0,0,1,0,0,1,1,0,1,1) построить МДНФ с помощью карт Карно.
z w
00
01
11
10
00
1
1
1
1
x
01
1
y
11
1
1
1
10
1
1
Рисунок
1

Значения функции перечислены в порядке естественного увеличения наборов значений переменных, рассматриваемых как четырехразрядные двоичные числа.
Изобразим карту Карно для данной функции, проставляя в ней только единичные значения.
Разобьем единицы по группам, как показано на рисунке1. Тогда соответствующая этому разбиению
МДНФ1 =
w x
![]() x z w x y z
x z w x y z
z w
00
01
11
10
00
1
1
1
1
x
01
1
y
11
1
1
1
10
1
1
Рисунок
2
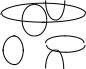
Соответствующая этому разбиению
МДНФ2 = w x z w x y z
z w
00
01
11
10
00
1
1
1
1
x
01
1
11
1
1
1
10
1
1
Рисунок
3
 y
y
МДНФ3 = w x x z w x y
z w
00
01
11
10
0
1
1
1
1
x
01
1
y
11
1
1
1
10
1
1
Рисунок
4
 0
0
МДНФ4 = w x z w x y
Другие варианты разбиения не приведут к более коротким ДНФ. Таким образом для данной функции получено четыре минимальных ДНФ.
Задания для самостоятельного решения:
Задание №1
Пусть дана функция от четырёх переменных f(x, y, z, w). Найти МДНФ функции методом Куайна.
Задание №2
Для функции от четырёх переменных f(x,y,z,w) построить МДНФ с помощью карт Карно.
Варианты заданий:
Вариант №1
f(x,y,z)=(0,5,8,9,10,12,13)
f(x,y,z)=(0,8,10,11,13,15)
Вариант №2
f(x,y,z)=(1,2,3,12,13,14,15)
f(x,y,z)=(2,3,7,8,10,11,12,15)
Вариант №3
f(x,y,z)=(0,4,6,7,8,10,13,15)
f(x,y,z)=(2,3,7,8,10,11,13,15)
Вариант №4
f(x,y,z)=(0,4,5,6,7,14,15)
f(x,y,z)=(0,3,7,8,9,10,11,12,15)
Вариант №5
f(x,y,z)=(2,4,7,9,10,14,15)
f(x,y,z)=(0,2,3,5,11,12,15)
Вариант №6
f(x,y,z)=(0,2,4,7,8,10,13,15)
f(x,y,z)=(3,6,8,9,12,13,15)
Вариант №7
f(x,y,z)=(2,4,7,9,10,11,13,15)
f(x,y,z)=(0,2,3,4,5,9,10,12)
Вариант №8
f(x,y,z)=(5,7,8,9,10,11,15)
f(x,y,z)=(2,3,4,9,10,11,14,15)
Вариант №9
f(x,y,z)=(0,2,4,8,12,14,15)
f(x,y,z)=(2,3,4,6,7,9,11,12)
Вариант №10
f(x,y,z)=(5,6,7,8,9,10,11,12,13)
f(x,y,z)=(3,5,7,10,11,12,13,14)
Вариант №11
f(x,y,z)=(1,2,3,4,9,11,12,14)
f(x,y,z)=(3,4,5,6,11,13,15)
Вариант №12
f(x,y,z)=(0,1,2,6,10,12,13,14)
f(x,y,z)=(2,3,4,8,12,14,15)
Вариант №13
f(x,y,z)=(1,2,4,5,9,10,13,14)
f(x,y,z)=(0,3,4,6,7,11,12,15)
Вариант №14
f(x,y,z)=(0,1,5,6,8,11,12)
f(x,y,z)=(2,3,7,8,10,13,14,15)
Вариант №15
f(x,y,z)=(1,2,3,4,9,11,12,14)
f(x,y,z)=(3,4,6,11,13,15)
Вариант №16
f(x,y,z)=(0,2,3,4,10,11,12,15)
f(x,y,z)=(3,4,5,9,11,13,15)
Вариант №17
f(x,y,z)=(1,2,3,4,7,8,9,11,12,14)
f(x,y,z)=(1,2,3,4,6,11,13,15)
Вариант №18
f(x,y,z)=(2,3,7,9,11,12,14)
f(x,y,z)=(2,4,5,8,11,13,15)
Вариант №19
f(x,y,z)=(1,2,3,4,5,11,13,14)
f(x,y,z)=(2,4,5,6,7,10,15)
Вариант №20
f(x,y,z)=(6,7,8,9,10,14,15)
f(x,y,z)=(0,3,5,6,7,11,12,13)
Практическая работа №9
Тема: Основные понятия теории графов.
Задание №1
Дан граф T:
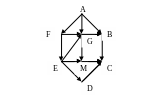
Задать данный граф матрицей смежности и инцидентности.
Решение:
Матрица инцидентности – это прямоугольная матрица, число строк которой равно числу вершин, количество столбцов – числу дуг (рёбер) графа. На пересечении строки и столбца ставится 1, если вершина является началом дуги, -1 – если концом дуги, 0 – если вершина и дуга не инцидентны.
-
AB
AG
AF
FE
FG
GB
GM
EG
EM
ED
DC
MC
BC
A
1
1
1
0
0
0
0
0
0
0
0
0
0
B
-1
0
0
0
0
-1
0
0
0
0
0
0
1
C
0
0
0
0
0
0
0
0
0
0
-1
-1
-1
D
0
0
0
0
0
0
0
0
0
-1
1
0
0
E
0
0
0
-1
0
0
0
1
1
1
0
0
0
F
0
0
-1
1
1
0
0
0
0
0
0
0
0
G
0
-1
0
0
-1
1
1
-1
0
0
0
0
0
M
0
0
0
0
0
0
-1
0
-1
0
0
1
0
Матрица смежности – это квадратная матрица, размер которой определяется числом вершин в графе. На пересечении строки и столбца ставится 1, если вершины инцидентны и 0 в противном случае.
-
A
B
C
D
E
F
G
M
A
0
1
0
0
0
1
1
0
B
1
0
1
0
0
0
1
0
C
0
1
0
1
0
0
0
1
D
0
0
1
0
1
0
0
0
E
0
0
0
1
0
1
0
1
F
1
0
0
0
1
0
1
0
G
1
1
0
0
1
1
0
1
M
0
0
1
0
1
0
1
0
Задание №2
Для данного графа (см. задание №1) вычислить хроматическое число h(T).
Решение:
Выделяем вершинно пустые подграфы графа, т.е. подмножества не инцидентных вершин:
E1={F, B, M, D}, E2={A, E, C}, E3={F, C}, E4={A, M, D}, E5={G, D}, E6={G, C},
E6={F, M}, E8={B, E}.
Строим двумерную таблицу,число строк которой равно числу подграфов, а число столбцов – числу вершин. На пересечении столбца и строки ставим единицу, если вершин содержится в подграфе.
Определяем покрытие столбцов строками, т.е. в каждом столбце должна быть хотя бы одна единица. Каждое покрытие порождает раскраску. Покрытие минимальной мощности определяет хроматическое число графа.
-
A
B
C
D
E
F
G
M
E1
1
1
1
1
E2
1
1
1
E3
1
1
E4
1
1
1
E5
1
1
E6
1
1
E7
1
1
E8
1
1
Минимальное покрытие столбцов строками является множество {E1, E2, E5}. Следовательно, хроматическое число графа h(T)=3

