Оглавление:

1. Множества и их спецификация……………………………………………………3

2. Функции и отображения…………………………………………………………...12

3. Отношения………………………………………………………………………….20

4. Переключательные функции. Способы задания…………………………………25

5. Специальные разложения ПФ……………………………………………………..29

6. Теорема о функциональной полноте………………………………………………32

7. Минимизация ПФ и неполностью определённых ПФ……………………………36

8. Минимизация ПФ и неполностью определённых ПФ методами, основанными на геометрическом представлении функций алгебры логики……………………40

9. Основные понятия теории графов………………………………………………….44

10. Маршруты, циклы, связность………………………………………………………49

Практическая работа №1.

Тема: Множества и их спецификация.

Задание №1.

Даны множества:

А = –1; 0; 1,

В = –2; 0) – полуинтервал на числовой оси,

С = –0.5; 2 - отрезок на числовой оси.

Найти:

АВ, АВС, АВ, ВС, АВС, A \ B, B \ A, A \ C, C \ A, (А \ В) \ С, А \ (В \ С), А  B, A  B  C.

Изобразить на плоскости: А  В, А  С, В  С. Найти , считая универсальным множеством множество всех вещественных чисел.

Решение:

Объединением двух множеств A и B называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B, поэтому:

АВ = –2; 0; 1

АВС = –2; 2

Пересечением двух множеств A и B называется множество элементов, принадлежащих одновременно и A, и B, поэтому:

АВ = –1

ВС = –0.5; 0)

АВС =  – пустое множество

Относительным дополнением множества B до множества A называется множество тех элементов A, которые не являются элементами B, поэтому

А \ В = 0; 1

В \ А = –2; –1); (–1; 0)

А \ С = –1

С \ А = –0.5; 0); (0; 1); (1; 2

(A \ B) \ C = 

A \ (B \ C) = {0; 1}

Симметрической разностью двух множеств A и B называется объединение двух разностей A \ B и B \ A, а абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, поэтому:

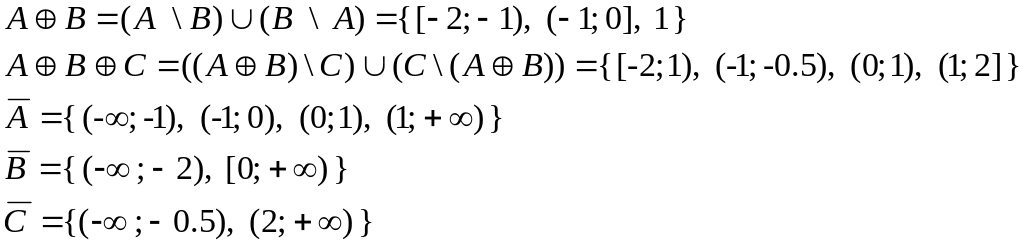
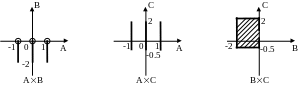Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b) таких, что и , поэтому:

Задание№2

Для заданного семейства множеств где Г – заданное индексное множество, найдите объединение и пересечение всех множеств семейства, т.е. и (по всем возможным индексам ).

{A_k}_kℝ, где для всякого вещественного индекса k множество

А_k={ (x, y):  |x|+|y| ≤ |γ| и x, yℝ }.

Решение: рассмотрим множества А_k для некоторых фиксированных индексов k.

При k=0 множество А₀={ (x, y): |x|+|y| ≤ 0}={(0;0)} – центр вещественной плоскости.

При k=0.5 и k= –0.5 А_0.5=А_‑0.5={ (x, y): |x|+|y| ≤ 0.5} – ромб в центре вещественной плоскости с диагоналями, равными 1 и направленными вдоль осей координат.

При k=2 и k= –2 А₂=А_‑2={ (x, y): |x|+|y| ≤ 2} – ромб с диагоналями, равными 4 и т. д..

При увеличении абсолютной величины индекса k диагонали ромба, расположенного в центре вещественной плоскости, увеличиваются и при |k|→+ ромб А занимает всю вещественную плоскость. Таким образом, объединение по всем вещественным индексам k равно = ℝ  ℝ = ℝ² – вся вещественная плоскость, а пересечение по всем вещественным индексам k равно – центр вещественной плоскости.

Задание№3

Докажите тождество, используя только определения операций над множествами:

Решение: (1) Пусть , тогда . Отсюда следует, что 1)  и или 2)  и . В первом случае из того, что следует, что х принадлежит также объединению множества А с любым другим множеством, в том числе и множеством В, т.е. . Но в то же время и, следовательно, х принадлежит также объединению с любым другим множеством, в том числе и множеством , т.е. . Таким образом, , т.е. . Аналогично во втором случае: из того, что следует, что х принадлежит также и . И в то же время, поскольку , то х принадлежит также объединению , с любым другим множеством, в том числе и множеством , т.е. . И также как в первом случае имеем: , тем самым .

(2) Пусть теперь . Тогда , отсюда . Следовательно, если , то , т.е. . Если же , то и значит . Таким образом, , что равносильно тому, что . Из (1) и (2) следует справедливость тождества.

Задание№4

Докажите тождество, используя диаграммы Эйлера-Венна.

Р ешение: Изобразим диаграмму для левой части тождества по шагам:

Теперь диаграмму правой части по шагам:

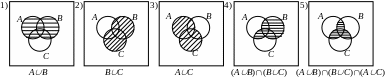
Ввиду того, что заштрихованные области, полученные на последнем шаге для левой и правой части тождества, одинаковы, можно заключить, что исходное выражение верно.

Задания для самостоятельного решения:

Задание №1

Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

Задание №2

Для заданного семейства множеств где Г – заданное индексное множество, найдите объединение и пересечение всех множеств семейства, т.е. и (по всем возможным индексам ).

Задание №3

Докажите тождества, используя только определения операций над множествами.

Задание №4

Докажите тождество, используя диаграммы Эйлера – Венна.

Варианты заданий:

Вариант№1

1. А = (0; 2] – полуинтервал на числовой оси

В = [1; 5] – отрезок числовой оси

С = (–1; 2) – интервал на числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4. . (А \ В) (В \ С) (В \ А) (С \ В) = А С

Вариант№2

1. А = {0, 1, 2, 3}– четырехэлементное множество

В = [–3; 3] – отрезок числовой оси

С = (-2; 2) – интервал на числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4. (А \ В) (В \ С) (С \ А) = (В \ А) (С \ В) (А \ С)

Вариант №3

1. А = (–1; +∞)– интервал на числовой оси

В = (–∞; 10] – полуинтервал на числовой оси

С = [–5; +15] – отрезок числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4. (А В) (С D) = В С, если А В = D и C D = A

Вариант №4

1. А = (–∞; 2]– полуинтервал на числовой оси

В = [–3; 3] – отрезок числовой оси

С = (0; 4) – интервал на числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4.

Вариант №5

1. А = (–2; 3) – интервал на числовой оси

В = [0; 4] – отрезок числовой оси

С = {2; 3} – двухэлементное множество

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

Если

4.

Вариант №6

1. А = [–5; 4]– отрезок числовой оси

В = (-∞; ∞)– интервал на числовой оси

С = (–1; 0] – полуинтервал на числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4.

Вариант №7

1. А = (2; 5]– полуинтервал на числовой оси

В = (0; 1)– интервал на числовой оси

С = {–2; -1; 0} – трехэлементное множество

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

где U – универсальное множество

4.

Вариант №8

1. А = (–1; 1)– интервал на числовой оси

В = [1; 2] – отрезок числовой оси

С = (–∞; 1] - полуинтервал на числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4.

Вариант №9

1. А = (5; 15] – полуинтервал на числовой оси

В = [5; 10] – отрезок числовой оси

С = {4; 5; 6} – трехэлементное множество

2. , где ℕ – множество всех натуральных чисел и  kℕ

3. если 

если

4.

Вариант №10

1. А = (0; 3) – интервал на числовой оси

В = [–1; 3] – отрезок числовой оси

С = (–1; 0] - полуинтервал на числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4.

Вариант №11

1. А = [–5; 2) – полуинтервал на числовой оси

В = [–5; 5] – отрезок числовой оси

С = (–1; 1) - интервал на числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

Если

4.

Вариант №12

1. А = (0; 5) – интервал на числовой оси

В = {-2, 0; 1; 2} – четырехэлементное множество

С = [–1; 1] - отрезок числовой оси

2. , где ℕ – множество всех натуральных чисел и  kℕ

3.

4.

Вариант №13

1. А = (–∞; ∞) – интервал на числовой оси

В = [0; +∞) – полуинтервал на числовой оси

С = (–∞; 5) - интервал на числовой оси

2. , где ℕ– множество всех натуральных чисел и  kℕ

3.

4.

Вариант №14

1. А=[– ; 3) – полуинтервал на числовой оси

В=[3; 10] – отрезок числовой оси

С=(3; + ) – интервал на числовой оси

2. {А_k}_kℝ, где ℝ – множество всех вещественных чисел и k ℝ

3. (A B) \ C=(A \ C) (B \ C)

(A  B)  (C  D)    (A  C)  (B  D)

4. (A  (A \ B))   = 

Вариант № 15

1. А=[–11; 1] –отрезок числовой оси

В=[–1; 3) – полуинтервал на числовой оси

С=(-2; 2) – интервал на числовой оси

2. {А_k}_{k ℝ}, где ℝ – множество всех вещественных чисел и k ℝ

3. A \ (B  C) = (A \ B)  (A \ C); (A \ B)  C = (A  C) \ (B  C)

4. ((A  C)  (B  D)) 

Вариант №16

1. А = (–0; 1) –интервал на числовой оси

В = {–1; 0; 1} – трехэлементное множество

С = [5; 10] – отрезок числовой оси

2. {А_k}_{k ℝ}, где ℝ – множество всех вещественных чисел и k  ℝ

3.

4.

Вариант №17

1. А=(-1; 0] – полуинтервал на числовой оси

В=(0; 1) – интервал на числовой оси

С={-5;- 1; 1} – трехэлементное множество

2. {А_k}_{k ℝ}, где ℝ – множество всех вещественных чисел и k ℝ

3.

4.

Вариант №18

1. А= {–1; 0; 1} – трехэлементное множество

В=(–1; 0.5) – интервал на числовой оси

С=[0; 1] – отрезок числовой оси

2. {А_k}_kℝ, где ℝ – множество всех вещественных чисел и k ℝ

A_k = {xℝ : x² ≥ k² + 1 }

3.

4.

Вариант №19

1. А= [–6; +6) – полуинтервал на числовой оси

В=[–10; 2] –отрезок на числовой оси

С={-1} – одноэлементное множнство

2. {А_k}_kℝ, где ℝ – множество всех вещественных чисел и k ℝ

A_k = {x ℝ: x² +1< k² }

3.

4.

Вариант № 20

1. А= (–1; 4) – интервал на числовой оси

В=[0; 1] – отрезок числовой оси

С=(-2; 0] – полуинтервал на числовой оси

2. {А_k}_kℝ, где ℝ – множество всех вещественных чисел и  k ℝ

A_k = { (x, y): |x| + |y|  ≥  |k|, где x, y ℝ }

3.

4.