
ЛИСТ ДЛЯ ЗАМЕЧАНИЙ
ОГЛАВЛЕНИЕ
1 ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 4
2 ДВОЙСТВЕННАЯ ЗАДАЧА 7
3 ЗАДАЧА О РАСПРЕДЕЛЕНИИ КАПИТАЛОВЛОЖЕНИЙ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 9
4 ЗАДАЧА О ЗАМЕНЕ ОБОРУДОВАНИЯ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 13
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 18
1 Задача линейного программирования
Задача о выпуске продукции при ограниченных ресурсах (11 вариант).
Мебельная фабрика выпускает два вида изделий: шкафы и столы. В производстве применяется оборудование трех видов: фрезерные, сверлильные и шлифовальные станки. Нормы времени работы каждого вида оборудования в час, необходимые для изготовления одного изделия каждого вида, а также ресурсы рабочего времени для каждого вида оборудования приведены в таблице 1:
Таблица 1
Изделие |
Станки
|
Прибыль |
||
Фрезерные |
Сверлильные |
Шлифовальные |
||
Шкафы |
a1 = 3 |
a2 = 1 |
a3 = 2 |
С1 = 10 |
Столы |
b1 = 5 |
b2 = 3 |
b3 = 1 |
С2 = 27 |
Ресурс времени |
Т1 = 238
|
Т2 = 118
|
Т3 = 123
|
|
Фабрика получает прибыль от изготовления одного шкафа в размере С1 и одного стула С2.
Требуется определить план выпуска изделий каждого вида, при котором время работы оборудования не превышало бы допустимого ресурса и была получена наибольшая общая прибыль.
Решение:
Целевая функция, обеспечивающая максимальную прибыль, будет выглядеть следующим образом:

где x1 – количество шкафов в плане выпуска, а x2 – стульев.
Система ограничений будет выглядеть так:
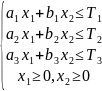
Для решения приведём задачу к каноническому виду путем введения дополнительных неотрицательных переменных x3, x4, x5. После этого система ограничений примет следующий вид:
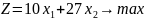
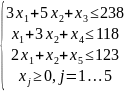
Решим задачу симплексным методом (табл.2).
Таблица 2
БП |
СБj |
10 |
27 |
0 |
0 |
0 |
bi |
bi/aip |
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
||||
x3 |
0 |
3 |
5 |
1 |
0 |
0 |
238 |
238/5 |
|
x4 |
0 |
1 |
3 |
0 |
1 |
0 |
118 |
118/3 |
Q |
x5 |
0 |
2 |
1 |
0 |
0 |
1 |
123 |
123 |
|
|
|
|
P |
|
|
|
|
|
|
|
Δ |
-10 |
-27 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
БП |
СБj |
10 |
27 |
0 |
0 |
0 |
bi |
bi/aip |
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
||||
x3 |
0 |
4/3 |
0 |
1 |
-5/3 |
0 |
124/3 |
31 |
Q |
x2 |
27 |
1/3 |
1 |
0 |
1/3 |
0 |
118/3 |
118 |
|
x5 |
0 |
5/3 |
0 |
0 |
-1/3 |
1 |
251/3 |
251/5 |
|
|
|
P |
|
|
|
|
|
|
|
|
Δ |
-1 |
0 |
0 |
9 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
БП |
СБj |
10 |
27 |
0 |
0 |
0 |
bi |
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
|||
x1 |
10 |
1 |
0 |
3/4 |
-5/4 |
0 |
31 |
|
|
x2 |
27 |
0 |
1 |
-1/4 |
3/4 |
0 |
29 |
|
|
x5 |
0 |
0 |
0 |
-5/4 |
7/4 |
1 |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Δ |
0 |
0 |
3/4 |
31/4 |
0 |
|
|
|
Проверка:
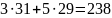
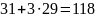
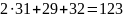
Решением задачи будет:
x1=31, x2=29, x3=0, x4=0, x5=32.
Z=1093.
