2.2. Донное сопротивление

Рис. 3. Течение в донной области при сверхзвуковых скоростях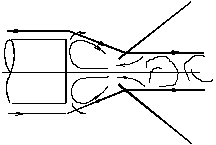

Донное сопротивление обусловлено разрежением в донной области тела. Коэффициент донного сопротивления численно равен коэффициенту донного давления, взятому с противоположным знаком. Донное разрежение зависит от скорости полета, состояния поверхности тела, его длины, т.е. от состояния пограничного слоя в области донного среза, и сужения кормовой части. Чем толще пограничный слой у донного среза (длинное тело или большая шероховатость), тем больше донное давление и меньше донное сопротивление. При сверхзвуковых скоростях с ростом числа разрежение в донной области тела увеличивается и при достаточно больших числах за дном возникает абсолютный вакуум.

Донное сопротивление для некоторых тел вращения может достигать 30% полного сопротивления. У тел вращения большого удлинения увеличение угла атаки до   5^ практически не влияет на величину донного давления. Более подробно с донным сопротивлением можно ознакомиться по книгам [1, 3].

Величину коэффициента донного сопротивления можно рассчитать по формуле:

,

где – относительная площадь донного среза.

Поправочный коэффициент , учитывающий отличие донного давления от абсолютного вакуума, зависит от числа и геометрических характеристик тела вращения и в общем случае рассчитывается по формуле (при k₁ 1), а при k₁ 1 . Здесь ( – удлинение корпуса ЛА).

При возрастании скорости полета и определенном сочетании параметров, входящих в формулу для расчета , расчетная схема предлагаемой программы расчета автоматически переходит от расчета величины по формуле, к постоянному значению . В этом случае на графике зависимости наблюдается нарушение плавности изменения коэффициента донного сопротивления.

2.3. Сопротивление трения

Проекцию главного вектора приложенных к ЛА касательных сил на направление невозмущенного потока называют сопротивлением трения. Наибольший вклад в сопротивление трения тел вращения дает его средняя цилиндрическая часть. Величина коэффициента сопротивления трения зависит от состояния пограничного слоя.

При сверхзвуковых скоростях полета длинного тела, ламинарный пограничный слой имеет место только в небольшой области, примыкающей к носовой оконечности тела, то есть практически на всей поверхности ЛА реализуется турбулентный режим течения. Место перехода пограничного слоя из одного состояния в другое может быть приближенно определено через отношение критического числа Рейнольдса к числу Рейнольдса в данной точке траектории ЛА. В расчетной схеме, принятой в программе расчета, за критическое число Рейнольдса принято значение .

Используя распространенный в аэродинамике прием, когда криволинейная внешняя поверхность реального ЛА заменяется плоской пластиной, эквивалентной по площади и той же протяженности по потоку, что и рассматриваемая поверхность тела вращения, расчетную формулу для определения сопротивления трения можно записать в виде:

,

где – коэффициент сопротивления трения плоской пластины в пограничном слое несжимаемой жидкости; – коэффициент, учитывающий отличие тела вращения от плоской пластины; – коэффициент, учитывающий сжимаемость среды; – относительная площадь боковой поверхности ЛА ( – полная площадь боковой поверхности и площадь миделевого сечения ).

При на поверхности ЛА существует смешанный пограничный слой. Поэтому среднее для ЛА значение местного коэффициента трения рассчитываем по следующей формуле:

,

в которой коэффициенты трения для ламинарного и турбулентного пограничных слоев определяются как:

, ;

Значение коэффициента зависит от удлинения тела вращения. Приведенная в книге [2] графическая зависимость аппроксимирована несколькими простейшими аналитическими формулами и использована в программе расчета. При расчете коэффициента также учитывается смешанный характер течения на поверхности ЛА:

,

где .

При имеет место чисто ламинарное обтекание всей поверхности ЛА, поэтому , .

Во всех расчетных формулах – число Рейнольдса, рассчитанное по параметрам атмосферы на заданной высоте

,

где – скорость звука на данной высоте; _н, Т_н – кинематический коэффициент вязкости и температура воздуха на заданной высоте (определяются с помощью таблицы стандартной атмосферы [1], в программе расчета параметры стандартной атмосферы заданы в виде аналитических выражений); l – полная длина ЛА.

С увеличением высоты полета коэффициент кинематической вязкости  непрерывно возрастает ввиду опережающего влияния уменьшения плотности, что приводит к росту толщины пограничного слоя и к увеличению . При постоянной высоте полета с ростом числа М_ коэффициент сопротивления трения убывает в связи с уменьшением толщины пограничного слоя.

Высота и скорость полета оказывают противоположное влияние на величины и скоростного напора . Поэтому при анализе их влияния на силу сопротивления трения следует учитывать интенсивность и направление (увеличение или уменьшение) изменения как , так и .

Число при увеличении H уменьшается и может стать даже меньше , то есть доля поверхности обтекаемой турбулентным пограничным слоем с ростом высоты полета уменьшается и на некоторой высоте пограничный слой на всей поверхности ЛА становится ламинарным. Характер влияния высоты полета на довольно сложный и необходимо быть особенно внимательным при анализе графиков, построенных для переменной высоты полета при одновременном увеличении скорости движения ЛА.