3.3. Общее решение дифференциальных уравнений длинной линии

Задача анализа цепей с распределенными параметрами обычно сводится к определению законов изменения токов и напряжений вдоль цепи, а также к исследованию частотных или временных характеристик цепи относительно внешних зажимов. С этой целью необходимо найти частные решения дифференциальных уравнений линии (1.44), (1.45) при соответствующих начальных и граничных условиях. Мы ограничимся рассмотрением однородной линии длиной l (рис.3), поскольку решение данных уравнений для неоднородных линий может быть получено только при некоторых частных видах зависимостей погонных параметров от координаты.

Рис.3. Схема замещения однородной длинной линии

Для решения дифференциальных уравнений линии используют операторный метод, который позволяет перейти от решения дифференциальных уравнений в частных производных для мгновенных значений токов и напряжений линии к решению обыкновенных дифференциальных уравнений, составленных относительно операторных изображений соответствующих токов и напряжений .

В курсе ОТЦ показано, что при нулевых начальных условиях, т.е. при и , задача сводится к решению двух дифференциальных уравнений:

уравнения, составленного относительно напряжения:

и уравнения, связывающего напряжение и ток:

Входящие в эти уравнения величины

называется операторным коэффициентом распространения, а параметры

Z₁(p) = R₁ + pL₁, Y₁(p) = G₁ + pC₁

называется операторным погонным сопротивлением и погонной проводимостью линии.

Таким образом, распределение операторных изображений токов и напряжений в линейной однородной инвариантной во времени цепи с распределенными параметрами описывается решениями линейного дифференциального уравнения второго порядка с постоянными коэффициентами, общее решение которого имеет вид

где А₁(р), А₂(р) — постоянные интегрирования, определяемые граничными условиями задачи, т.е. значениями неизвестных функций и в начале (x = 0) или в конце (x = l) линии.

Выражение для операторного изображения тока линии

где величина

называется операторным волновым сопротивлением линии.

Определяя значения постоянных интегрирования А₁(р), А₂(р), соответствующие тем или иным граничным условиям, и подставляя их в выражения для и , можно получить операторные изображения тока и напряжения в любом сечении линии при произвольном внешнем воздействии, а также найти любые частотные и временные характеристики исследуемой цепи.

3.4. Однородная длинная линия при гармоническом внешнем воздействии

Рассмотрим волновые процессы, происходящие в однородной длинной линии.

Распределение комплексных действующих значений напряжения и тока в однородной длинной линии, находящейся под гармоническим внешним воздействием, определяется выражениями

Эти выражения получаются из выражений для и путем замены комплексной частоты р на jω.

Входящие в выражения для и коэффициент распространения

и волновое сопротивление

являются комплексными величинами и зависят от частоты и погонных параметров линии.

Представим коэффициент распространения линии в алгебраической форме записи

а волновое сопротивление линии и постоянные интегрирования в показательной форме записи

и преобразуем каждое из входящих в выражения (8.10), (8.11) слагаемых в показательную форму:

Перейдем от комплексных действующих значений напряжения и тока к мгновенным значениям:

Отсюда следует, что установившиеся значения напряжения и тока в произвольном сечении линии, находящейся под гармоническим внешним воздействием, можно представить в виде алгебраической суммы двух подобных по структуре, но отличающихся знаками перед коэффициентами α и β составляющих:

где

При фиксированном x, т.е. в любой фиксированной точке линии, каждая из составляющих тока и напряжения представляет собой гармоническую функцию времени t.

Сумма двух гармонических функций времени, имеющих одинаковую частоту, является гармонической функцией времени той же частоты. Поэтому напряжение и ток во всех сечениях линии изменяются по гармоническому закону с частотой внешнего воздействия ω. Как видно из рис.4, а, для каждого фиксированного момента времени напряжение u_пад(x,t) изменяется вдоль линии по гармоническому закону, причем амплитуда напряжения экспоненциально уменьшается с ростом x. При увеличении t точки функции u_пад(x,t), имеющие одинаковую фазу, смещаются вправо, т.к.

, т.е. с ростом координата растет.

Аналогичный вид имеют зависимости i_пад(x,t). Следовательно, u_пад(x,t) и i_пад(x,t) представляют собой волны напряжения и тока, распространяющиеся в направлении увеличения x. Эти волны называют падающими волнами напряжения и тока.

Из рассмотрения зависимостей u_отр(x,t) и i_отр(x,t) следует, что u_отр(x,t) и i_отр(x,t) представляют собой волны напряжения и тока, распространяющиеся в направлении уменьшения x, т.е. от конца линии к ее началу (рис.4, б). Эта волны называются отраженными волнами напряжения и тока.

Таким образом, мгновенное значение напряжения в любой точке линии определяется суммой падающей и отраженной волн напряжения (8.17), а мгновенное значение тока — разностью падающей и отраженной волн тока (8.18). Положительные направления u_пад и u_отр выбраны одинаково (от верхнего проводника к нижнему), поэтому напряжения u_пад и u_отр суммируются; положительные направления токов i_пад и i_отр противоположны (падающая волна тока направлена от начала линии к концу, а отраженная от конца линии к началу), поэтому ток i_отр вычитается из тока i_пад.

Рис.4. Распределение напряжения падающей (а) и отраженной (б)

волн вдоль линии (t₃>t₂>t₁)

Совокупность падающей волны напряжения и падающей волны тока для краткости называют падающей волной, а совокупность отраженной волны напряжения и отраженной волны тока — отраженной волной.

Мы видим, что амплитуды напряжения и тока падающей и отраженной волн уменьшаются в направлении распространения волн. Величина α, характеризующая уменьшение амплитуды (действующего значения) падающей или отраженной волны на единицу длины линии,

называется коэффициентом ослабления. Убывание амплитуды волны связано с потерями энергии, поэтому для линии без потерь (R₁ = 0, G₁= 0) коэффициент ослабления α = 0, а коэффициент распространения является чисто мнимым: . Амплитуды падающей и отраженной волн напряжения и тока в линиях без потерь не зависят от координаты x и не изменяются вдоль линии.

Мнимая часть комплексного коэффициента передачи линии

характеризующая изменение фазы прямой и обратной волн на единицу длины линии, называется коэффициентом фазы. Для линии без потерь коэффициент фазы прямо пропорционален частоте:

Расстояние между двумя точками волны, фазы которых различаются на 2π, называется длиной волны в линии. Длина волны в линии λ определяется значением коэффициента фазы. Действительно, изменение фазы падающей или отраженной волны на участке линии длиной λ

откуда

Для линии без потерь .

Скорость перемещения вдоль линии точки волны, фаза колебания в которой остается неизменной, называется фазовой скоростью волны. Для падающей волны условие постоянства фазы записывается в виде

откуда фазовая скорость

Для линии без потерь фазовая скорость падающей и отраженной волн не зависит от частоты:

Используя выражения (8.21) и (8.22), получаем соотношения между фазовой скоростью и длиной волны в линии:

Из выражения (8.24) следует, что за время, равное периоду внешнего воздействия Т, падающая и отраженная волны перемещаются на расстояние, равное длине волны λ.

В связи с тем, что напряжение и ток в любом сечении линии можно рассматривать как результат наложения двух волн — падающей и отраженной, нетрудно прийти к заключению, что первое и второе слагаемые, входящие в выражения (8.10), (8.11), представляют собой комплексные действующие значения напряжения или тока падающей и отраженной волн:

где

Из выражений (8.25) и (8.26) следует, что волновое сопротивление однородной линии Z_в является коэффициентом пропорциональности между комплексными напряжением и током падающей или отраженной волны:

Таким образом, волновое сопротивление однородной линии можно рассматривать как комплексное сопротивление линии падающей или отраженной волнам в отдельности.

Волновое сопротивление линии без потерь имеет чисто резистивный характер:

Используя выражения (8.25), (8.26), можно установить физический смысл коэффициента γ. С этой целью найдем комплексные действующие значения напряжений падающей волны в точках, отстоящих одна от другой на расстоянии Δх:

Определяя натуральный логарифм отношения этих величин , получаем

Аналогичным образом можно записать

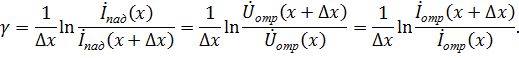
Таким образом, коэффициент распространения однородной длинной линии характеризует изменение комплексного действующего значения напряжения или тока падающей и отраженной волн, приходящееся на единицу длины линии.

Представляя комплексное действующее значение напряжения падающей волны в показательной форме

и используя выражения (8.14), (8.29), устанавливаем, что коэффициент ослабления линии α численно равен натуральному логарифму отношения действующих значений напряжения падающей волны, взятых в точках, отстоящих одна от другой на единицу длины линии:

а коэффициент фазы — разности фаз напряжений, измеренных в тех же точках:

Волновое сопротивление и коэффициент распространения называются волновыми параметрами линии. В общем случае коэффициент распространения и волновое сопротивление линии для падающей и отраженной волн могут иметь различные значения, поэтому линия произвольного вида характеризуется четырьмя волновыми параметрами. У однородной линии коэффициенты распространения и волновые сопротивления для падающей и отраженной волн, соответственно, имеют одинаковые значения, поэтому однородная линия характеризуется двумя волновыми параметрами.