
- •Теорема 1 (свойства счетных множеств).
- •4. Несчетные множества.
- •7. Иррациональность числа корень квадратный из 2.
- •8. Десятичные дроби, рациональные и иррациональные числа, свойство полноты действительных чисел.
- •Доказательство:
- •Предел подпоследовательности. Частичные пределы. Лемма Больцано-Вейерштрасса.
- •Свойства
- •Принцип математической индукции.
- •Второй замечательный предел
- •В. Предел функции, непрерывные функции.
- •Расширенное свойство предела суммы
В. Предел функции, непрерывные функции.
Определение предела функции по Коши и по Гейне. Односторонние пределы.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Определение
предела по Гейне. Число A называется пределом
функции f (x) в
точке a,
если эта функция определена в некоторой
окрестности точки a за
исключением, быть может, самой точки a,
и для любой последовательности ![]() такой,
что
такой,
что ![]() сходящейся
к числу a,
соответствующая последовательность
значений функции
сходящейся
к числу a,
соответствующая последовательность
значений функции ![]() сходится
к числу A.
сходится
к числу A.
Если функция f (x) имеет предел в точке a, то этот предел единственный.
Число A1 называется пределом
функции f (x) слева в
точке a,
если для каждого ε > 0 существует
δ > 0 такое, что для всех ![]() выполняется
неравенство
выполняется
неравенство ![]()
Число A2 называется пределом
функции f (x) справа в
точке a,
если для каждого ε > 0 существует
δ > 0 такое, что для всех ![]() выполняется
неравенство
выполняется
неравенство ![]()
Предел слева
обозначается  предел
справа –
предел
справа –  Эти
пределы характеризуют поведение функции
слева и справа от точки a.
Их часто называют односторонними
пределами.
Эти
пределы характеризуют поведение функции
слева и справа от точки a.
Их часто называют односторонними
пределами.
Свойства предела функции.

1. Предел постоянной величины равен самой постоянной величине:
![]()
2. Предел суммы двух функций равен сумме пределов этих функций:
![]() А
А
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы
Предел суммы нескольких функций равен сумме пределов этих функций:
![]()
Аналогично предел разности нескольких функций равен разности пределов этих функций.
3. Предел произведения функции на постоянную величину. Постоянный коэффициент можно выносить за знак предела:
![]()
4. Предел произведения двух функций равен произведению пределов этих функций:
![]()
Расширенное свойство предела произведения Предел произведения нескольких функций равен произведению пределов этих функций:
![]()
5. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Критерий Коши существования предела.
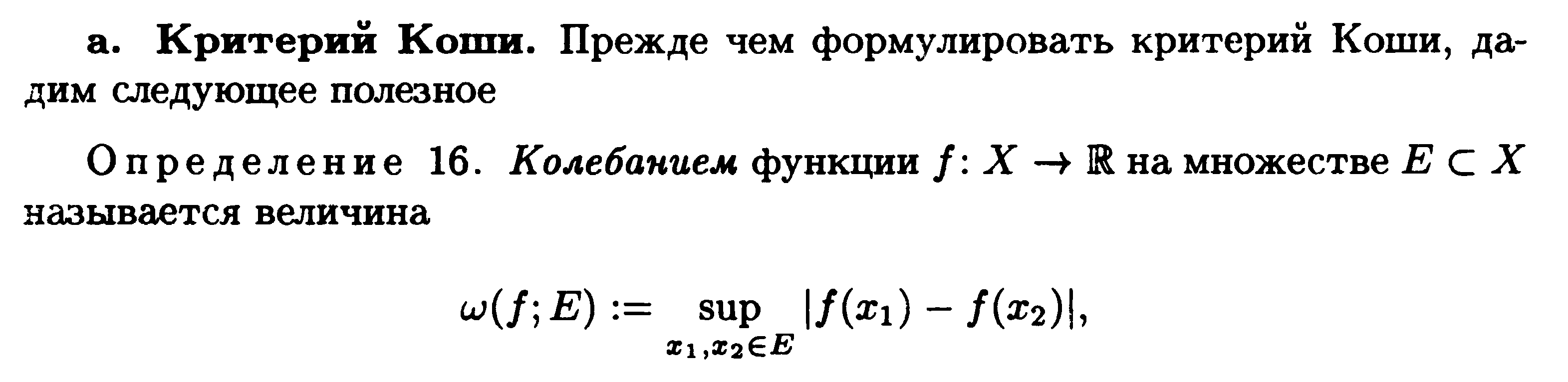


Монотонные функции и их пределы.

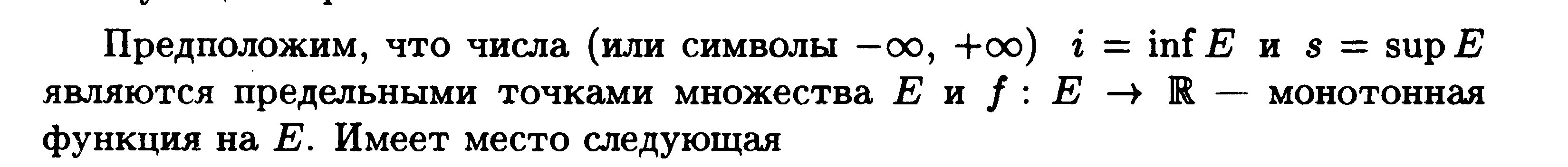


Сравнение бесконечно малых функций.

Непрерывность функции в точке (различные определения и их эквивалентность). Непрерывность функции на множестве, примеры.
точке окрестности





Арифметические операции над непрерывными функциями.
 Пусть
функции f (x)
и g (x)
непрерывны в точке х0.
Тогда функции f (x)
± g (x), f (x)·g (x)
и f (x)
: g (x)
также непрерывны в этой точке (в последнем
случае предполагается g (х0)
≠ 0).
Пусть
функции f (x)
и g (x)
непрерывны в точке х0.
Тогда функции f (x)
± g (x), f (x)·g (x)
и f (x)
: g (x)
также непрерывны в этой точке (в последнем
случае предполагается g (х0)
≠ 0).

Локальные свойства непрерывной функции (ограниченность, отделимость от нуля).


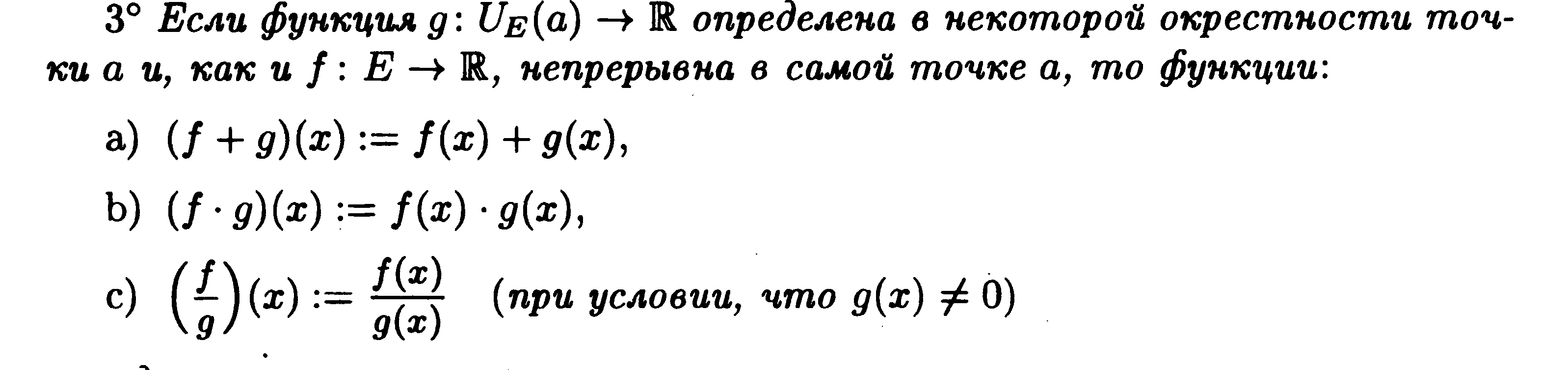


Глобальные свойства непрерывной функции. 1-ая теорема Больцано - Коши (о нуле функции).


2-ая теорема Больцано - Коши (о промежуточном значении).


1-ая теорема Вейерштрасса (об ограниченности функции).


2-ая теорема Вейерштрасса (о достижении экстремумов).

Равномерная непрерывность функции. Теорема Кантора.


Точки разрыва и их классификация.


Точки разрыва монотонной функции.
Обратная функция и ее свойства.
Непрерывность сложной функции.
