Свойства

-Ограниченность.

-Всякая неубывающая последовательность ограничена снизу.

-Всякая невозрастающая последовательность ограничена сверху.

-Всякая монотонная последовательность ограничена по крайней мере с одной стороны.

-Монотонная последовательность сходится тогда и только тогда, когда она ограничена с обеих сторон.

-Сходящаяся неубывающая последовательность ограничена сверху своим пределом.

-Сходящаяся невозрастающая последовательность ограничена снизу своим пределом.

8. Принцип математической индукции.

в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что, если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.

Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку. Тогда, если мы толкнём первую косточку, то все косточки в ряду упадут.

Формулировка : Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:  .

Пусть имеется семейство утверждений  . Пусть известно, что:

1.(база индукции)   справедливо;

2.(индукционный переход) из справедливости   вытекает справедливость  .

Тогда все утверждения   справедливы.

9. Число е.

Второй замечательный предел

Рассмотрим числовую последовательность  , где  ,   С ростом   основание степени уменьшается до единицы, а показатель растет до бесконечности, поэтому ничего конкретного о поведении   сказать нельзя. Для вычисления   воспользуемся выражением для бинома Ньютона:

.     (0.0.1)

В нашем случае

.

Из полученного выражения следует, что с увеличением   величина   растет. Действительно, перейдем от   к  . Это приведет к тому, что число слагаемых возрастет на одно. Кроме того, величина множителей, заключенных в скобки, тоже возрастет, так как  . Но если увеличивается число слагаемых и сами слагаемые растут, то  . Значит, числовая последовательность   монотонно возрастает.

Докажем теперь, что данная последовательность ограничена сверху. Заменим все скобки вида   единицей. Так как  , то

.

Кроме того  ,  ,...,  . Значит,

.

В правой части неравенства после цифры 2 стоит убывающая геометрическая прогрессия. Как известно, сумма   первых членов такой прогрессии равна: 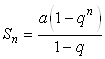 . В нашем случае  . С ростом   величина   будет, очевидно, стремится к единице. Значит,  , то есть, ограничено сверху.

Итак, мы получили, что  . Но так как   монотонно возрастающая последовательность ограниченная сверху, то она имеет предел:

Можно доказать, что данный предел справедлив не только для натуральных чисел, но и для любых значений  :

.

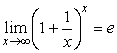Полученное выражение и называется вторым замечательным пределом.

 Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, т.е. докажем, что  . Рассмотрим два случая:

1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:  , где n = [x] - это целая часть x.

Отсюда следует:  , поэтому

.

Если  , то  . Поэтому, согласно пределу  , имеем:

.

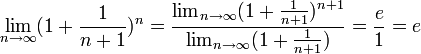
По признаку (о пределе промежуточной функции) существования пределов  .

2. Пусть  . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что   для любого x.