12. Интервальные оценки неизвестных параметров распределений (математического ожидания и дисперсии нормальнораспределенной генеральной совокупности)
На
практике ограничиться нахождением
«хороших» точечных оценок бывает обычно
недостаточно. Приближенное равенство
лишь указывает на то, что вместо
неизвестного параметра
можно использовать известное значение
оценки
.
Однако важно знать (хотя бы в вероятностном
смысле) величину совершаемой при этом
ошибки. Для этого прибегают к построению
интервальных оценок неизвестных
параметров.
Пусть
наблюдаемая величина
имеет функцию распределения
,
зависящую от неизвестного параметра
.
При интервальном оценивании параметра
ищут две такие статистики
и
(
и
- случайные величины!), для которых при
заданном
выполняется соотношение
.
В этом
случае интервал
называют
-доверительньм
интервалом
для
параметра
,
число
- доверительной
вероятностью
(надежностью, коэффициентом доверия),
и
- нижней и верхней доверительными
границами
соответственно.
Таким образом, -доверительный интервал — это случайный интервал, зависящий от выборки (но не от ), который содержит (накрывает) истинное значение неизвестного параметра с вероятностью . На практике обычно используют значения доверительной вероятности из небольшого набора близких к 1 значений (0,9; 0,95; 0,98; 0,99 и т. д.) и строят соответствующие им доверительные интервалы.
Построение доверительных интервалов для отдельных параметров распределения генеральной совокупности зависит как от вида закона распределения, так и от того, являются известными значения остальных параметров распределения или нет.
Если наблюдаемая случайная величина имеет нормальный закон распределения
с неизвестным математическим ожиданием
и известной
дисперсией
,
то доверительный
интервал для математического ожидания
имеет
вид:
,
где
- выборочное среднее;
- объем выборки; число
- такое значение аргумента функции
Лапласа
при
котором
.
Находят число
по заданной доверительной вероятности
из табл. П2.
Квантилью,
соответствующей вероятности
,
называется такое значение
,
при котором выполняется соотношение
,
где
– плотность вероятностей соответствующего
закона распределения (слово квантиль
– женского рода). Геометрическое
пояснение смысла квантили, отвечающей
вероятности
,
приведено на рис. 2.
Рис. 2. Геометрическое пояснение смысла
квантили
,
отвечающей вероятности
В этой терминологии число есть (1+)/2 - квантиль стандартного нормального N(0,1) закона распределения.
Если наблюдаемая случайная величина имеет нормальный закон распределения
с неизвестным математическим ожиданием
и неизвестной
дисперсией
,
то доверительный
интервал для математического ожидания
имеет вид:
где
- выборочная
дисперсия;
;
- объем
выборки; число
–
- квантиль распределения Стьюдента
с
(n—1)
степенью свободы. Находят квантиль
по заданным
и
из табл. ПЗ.
При
больших
(практически
при
)
распределение Стьюдента приближается
(в смысле слабой сходимости) к стандартному
нормальному закону распределения,
поэтому в этом случае
.
Доверительный интервал для дисперсии
наблюдаемой случайной величины
,
распределенной по нормальному закону
,
при известном
математическом
ожидании
имеет вид:
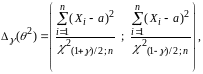
где
числа
есть
квантили распределения хи - квадрат
с n
степенями свободы соответственно.
Квантили распределения хи - квадрат
находят по заданным
и
из табл.П4.
Доверительный интервал для дисперсии наблюдаемой случайной величины , распределенной по нормальному закону , при неизвестном математическом ожидании
имеет вид:
где
- выборочная дисперсия, а
– соответствующие квантили распределения
.
При больших (практически при ) с использованием центральной предельной теоремы можно показать, что приближенным (асимптотическим) доверительным интервалом для дисперсии нормально распределенной случайной величины с неизвестным математическим ожиданием является интервал
Фактически
это означает, что для квантилей
распределения хи - квадрат
и
при
имеют место приближенные формулы:
Если
распределение наблюдаемой случайной
величины
произвольное (не обязательно нормальное),
то, используя асимптотическую нормальность
выборочных моментов, можно показать,
что при больших объемах выборки
приближенными
(асимптотическими) доверительными
интервалами для математического ожидания
и
дисперсии
являются:
где
- выборочное
среднее;
- выборочная дисперсия;
;
- выборочный центральный момент четвертого
порядка.
Замечание:
Все приведенные доверительные интервалы,
рассчитанные для заданной выборки
,
являются обычными числовыми интервалами,
внутри которых неизвестный параметр
находится в
100%
случаев.