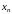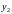1. Классическое определение вероятности Если события и несовместны , то

.

Размещением из N элементов некоторого множества по M элементов называется любой упорядоченный набор из M элементов данного множества. Число всех размещений равно .

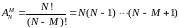Если в упорядоченном наборе элементы могут повторяться, то этот набор называется размещением с повторениями. Число размещений с повторениями: равно .

Перестановкой из N элементов некоторого множества называется размещение из N элементов по N. Число всех перестановок равно .

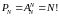Сочетанием из N элементов некоторого множества по M элементов называется любое подмножество мощности M. Число всех сочетаний равно .

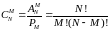2. Вероятности случайных событий (теоремы сложения и умножения вероятностей)

5°. Теорема сложения вероятностей.

Для любых событий (не обязательно несовместных)

.

Теорема (умножения вероятностей).

Пусть  некоторые события, определенные на одном и том же вероятностном пространстве , для которых . Тогда

.

3. Формула Бернулли

формула полной вероятности

. формула Байеса

. формула Бернулли.

4. Функция распределения случайных величин и ее свойства

Функцией распределения случайной величины называется функция , определенная при каждом равенством:

.

F0). для любого .

F1). Функция распределения является функцией неубывающей: .

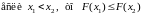F2). .

F3). Функция распределения является функцией непрерывной слева, то есть для любого

,

где - предел слева функции распределения в точке х.

F4). Для любого

,

где - предел справа функции распределения в точке х, - величина скачка функции распределения в точке .

F5). Для любого

.

F6). Вероятность попадания случайной величины в интервал 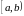определяется как приращение функции распределения на этом интервале:

для любых

.

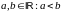
F7). .

F8). .

F9). .

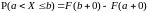5. Дискретные случайные величины и их числовые характеристики

						(2.1)

закон распределения

,

.

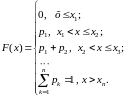
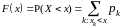
6. Плотность вероятности случайных величин и ее свойства (равномерный и нормальный законы распределения)

. (2.3)

При этом функция называется плотностью вероятностей

Свойства плотности вероятностей

f1). Плотность вероятностей является функцией неотрицательной:

для любого .

f2). Площадь под графиком плотности вероятностей равна единице:

- условие нормировки.

f3). Вероятность попадания непрерывной случайной величины в интервал определяется как интеграл от плотности вероятностей по этому интервалу: для любых

. (2.6)

7. Непрерывные случайные величины и их числовые характеристики

,

1. Равномерная случайная величина.

,

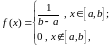
3. Нормальная (гауссовская) случайная величина.

.

,

8. Дискретные случайные векторы и их числовые характеристики (теорема сложения дисперсий)

Функцией распределения случайного вектора 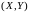называется функция двух действительных переменных и , определяемая при каждом равенством:

. (3.1)

			…		(3.2)
			…
			…
			…

.

где в соответствии с (3.3) вероятность получается суммированием в -ой строке таблицы (3.2) вероятностей , .

.

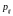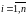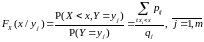Основными числовыми характеристиками двумерного случайного вектора являются:

• математическое ожидание - вектор, координатами которого являются математические ожидания случайных величин и ;

• дисперсия 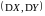- вектор, координатами которого являются дисперсии случайных величин и ;

• корреляционный момент

. (3.17)

• корреляционную матрицу .

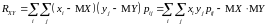
Теорема 3 (теорема сложения дисперсий).

Для любых действительных чисел и любых случайных величин и , имеющих конечную дисперсию

.

В частности, если и случайные величины и являются некоррелированными, то имеет место свойство аддитивности дисперсии: