
Пример использования нечетких множеств в иис
Рассмотрим задачу вычисления перспективного ассортимента продукции склада. Под перспективным ассортиментом в данном случае понимается набор товаров, которые заведомо будут иметь спрос среди потребителей.
Успешное решение задачи нахождения перспективного ассортимента позволяет повысить обоснованность принятия решений при закупках продукции.
В качестве исходной информации для решения задачи потребуется:
![]() — множество
товаров.
— множество
товаров.
![]() — множество
признаков
товаров.
— множество
признаков
товаров.
![]() — множество
магазинов в которые осуществляются
поставки продукции со склада.
— множество
магазинов в которые осуществляются
поставки продукции со склада.
Требуется определить перспективный ассортимент склада, то есть набор хj для удовлетворения предполагаемых запросов из Z.
Модель строится при следующих допущениях:
на рынке действуют поставщик и потребители — соответственно склад и магазины.
коммерческие запросы от потребителей
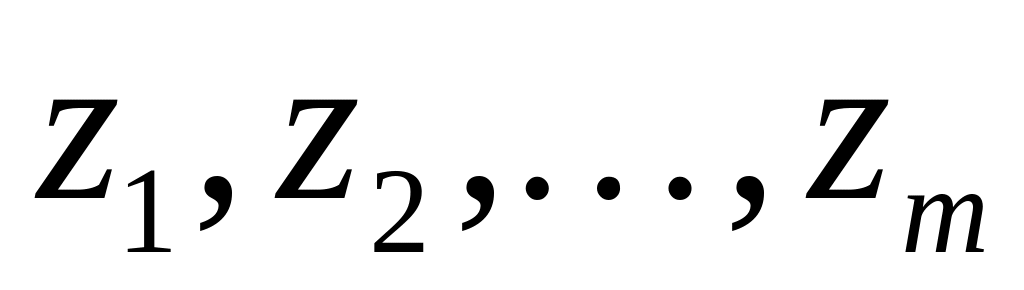 рассматриваются и по возможности
удовлетворяются независимо от времени
их поступления.
рассматриваются и по возможности
удовлетворяются независимо от времени
их поступления.обслуживание потребителей определяется весовой функцией розничных организаций с помощью экспертной оценки по итогам предыдущей коммерческой деятельности.
товары
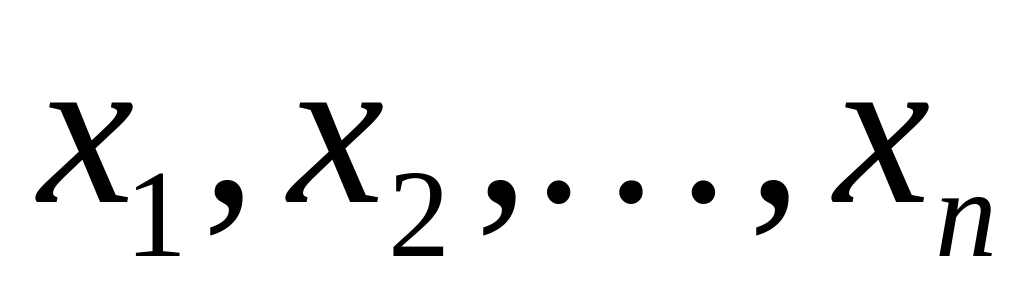 характеризуются р
признаками.
характеризуются р
признаками.степени принадлежности признаков
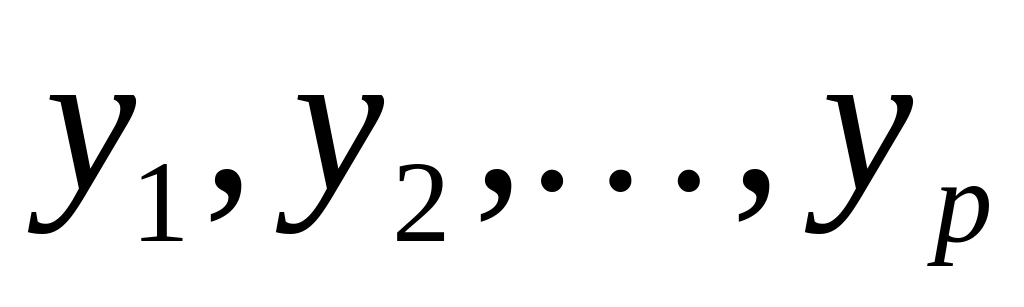 товарам варьируются между отдельными
товарами
.
товарам варьируются между отдельными
товарами
.один товар предпочитается другому всякий раз, когда его признаки уi по степени важности более близки к оценке потребителя zi.
Пусть
![]() — функция принадлежности нечеткого
бинарного отношения R,
определяемая с помощью эксперта.
— функция принадлежности нечеткого
бинарного отношения R,
определяемая с помощью эксперта.
Отношение R представляется в матричной форме следующим образом:
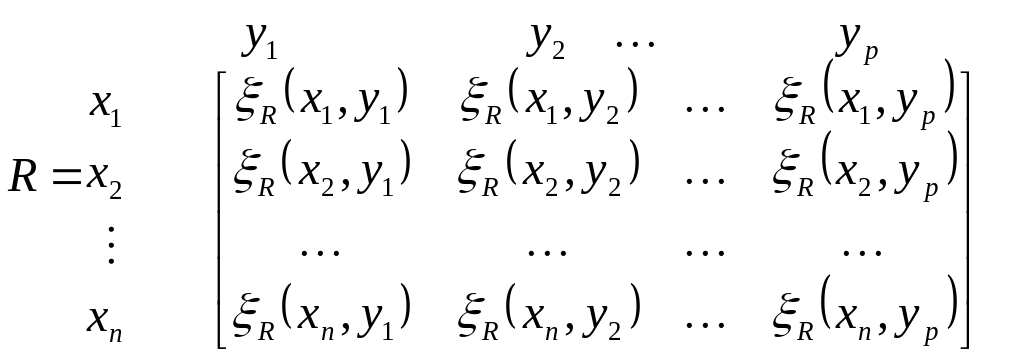
В этой матрице элементы каждой строки выражают относительные степени принадлежности признаков определенным товарам. Чем выше значения, тем более важен признак.
Пусть
![]() — функция принадлежности нечеткого
бинарного отношения S.
Для всех
— функция принадлежности нечеткого
бинарного отношения S.
Для всех
![]() и всех
и всех
![]()
![]() равна степени совместимости потребителей
с признаком у.
Чем выше значения функции, тем более
данный признак совместим с конкретным
потребителем.
равна степени совместимости потребителей
с признаком у.
Чем выше значения функции, тем более
данный признак совместим с конкретным
потребителем.
В матричной форме это отношение имеет вид:
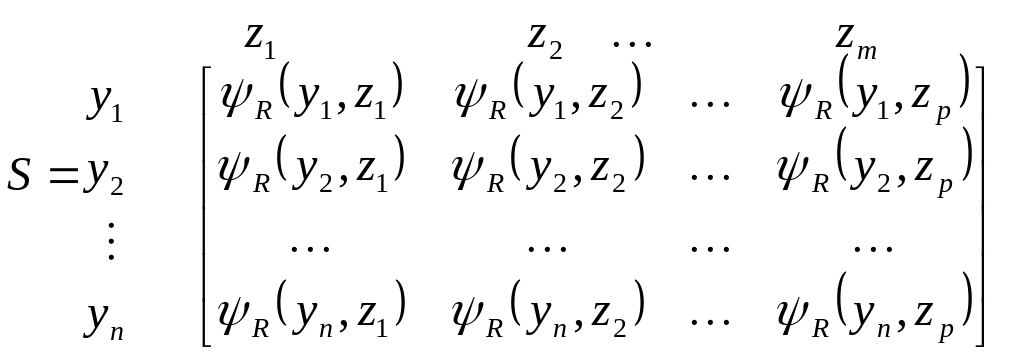
Значение матрицы S отражают относительные степени важности признаков yi при принятии магазином zj решения о закупке товара.
Из матриц R и S получаем матрицу Т:
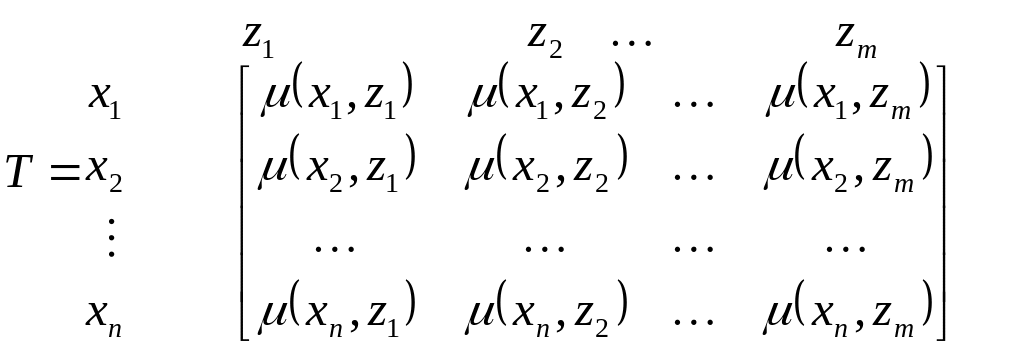
элементы, которой определяются функцией принадлежности:
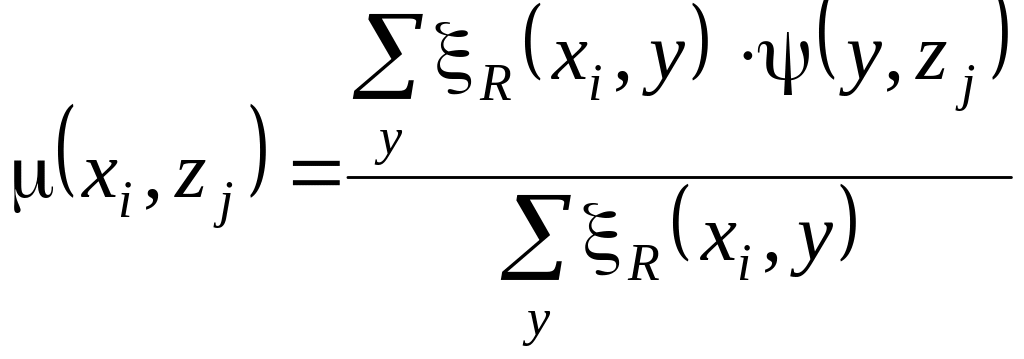 ,
,
для
всех
![]() ,
,
![]() ,
,
![]() .
.
Сумма
![]() равна степени нечеткого подмножества,
указывающей число важнейших признаков
у,
которое присуще товару х
с точки зрения
клиентов.
равна степени нечеткого подмножества,
указывающей число важнейших признаков
у,
которое присуще товару х
с точки зрения
клиентов.
Далее строится матрица:
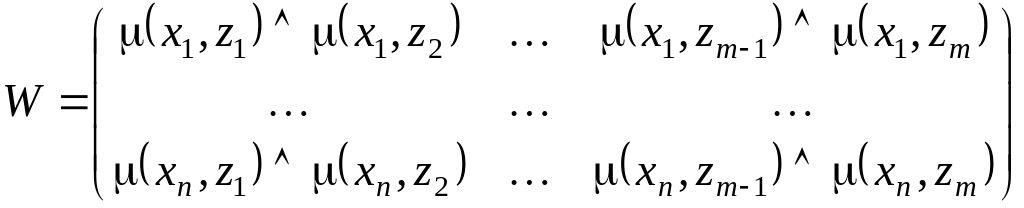 ,
,
где конъюнкция означает операцию попарного минимума.
Порог разделения l ассортимента ограничивается условием:
![]() .
.
После того как порог l выбран, можно для любого z определить уровневое множество:
![]() ,
,
![]() .
.
Пусть
![]() — весовая функция, задающая для каждого
магазина его вес по итогам предыдущей
деятельности.
— весовая функция, задающая для каждого
магазина его вес по итогам предыдущей
деятельности.
Ассортимент предприятия оптовой торговли описывается объединением уровневых множеств:
![]() .
.
Вычисление перспективного ассортимента помогает определить:
как оптимизировать товарный ассортимент (какие товары обязательно следует иметь при сохранении сложившейся структуры потребителей);
как изменить ассортиментную концепцию при заданном изменении зоны обслуживания, т.е. какие стратегические действия предпринять в случае выхода из числа обслуживаемых потребителей отдельных магазинов.
