ЛАБОРАТОРНА РОБОТА №3

3. Визначення геометричних характеристик поперечного перерізу

Мета роботи: визначення геометричних характеристик складного поперечного перерізу.

3.1 Загальні теоретичні положення

Для стандартних поперечних перерізів (кутника рівнобокого, швелера, двотавра) геометричні характеристики наведено в таблицях сортаментів. Для експериментального визначення геометричних характеристик профілі розбиваємо на декілька прямокутників, для кожного з яких відомі площа положення центра ваги, моменти інерції.

Д ля прямокутника статичний момент площі відносно даної осі:

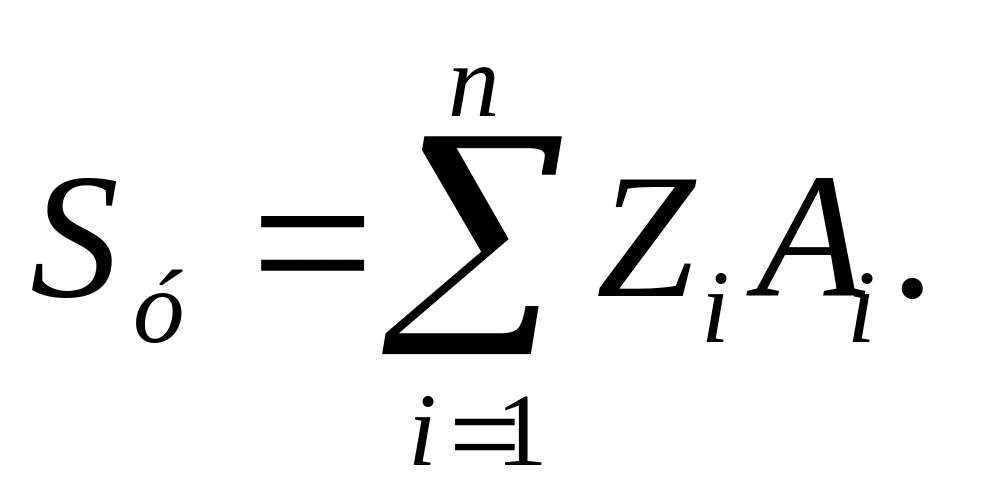
Осьові і відцентровий моменти інерції відносно головних центральних осей інерції:

Моменти опору:

Координати центра ваги складної плоскої фігури визначаємо за формулами:

де і – координати центра ваги простих профілів;

– площі поперечного перерізу простих профілів.

_{При цьому треба враховувати знаки переносу αi, bi відносно центральних осей простих профілів. Зазначимо, що осьові моменти інерції можуть набирати лише додатніх значень. Відцентрові моменти інерції в залежності від положення осей можуть бути додатніми, від’ємними або дорівнювати нулю. Відцентровий момент інерції відносно головних осех інерції (а осі симетрії є завжди головними) дорівнює нулю.}

_{Д ля кутника рівнобокого}

Для визначення положення головних центральних осей неси метричної фігури визначаємо за формулою:

_{при цьому від’ємні кути α0 відкладаються від осі z за годинниковою стрілкою.}

_{Головні осі інерції позначаються U (початкова вісь z) i V (початкова вісь у), а головні моменти інерції визначаються за формулою:}

_{О чевидно, що при Iz>Iy, момент}

_{де Vmax– відстань від осі U до найбільш віддаленої точки від осі U.}

Таблиця 3.1 Координати центра ваги складного перерізу

Профіль	Номер частини фігури	Площа	Координати центра ваги профілей системи ,	Статичні моменти площі відносно осей ,	,
	I
	II
	∑

Таблиця 3.2 Моменти інерції відносно центральних осей

Номер частини фігури

Пло-ща ,

Моменти інерції відносно центральних осей простих профілів

Моменти інерції відносно центральних осей складного поперечного переріза

І

ІІ

∑