3.3 Пример задачи прогнозирования с предварительной
обработкой данных
Задана выборка из 32 поквартальных значений за 1995-2002 годы, сформированных на основе бухгалтерской отчетности ООО «Вавилон». Требуется решить задачу построения математической модели типа «Инфляция-производство», анализирующую данные и формирующую связь между показателями экономического роста данного предприятия (входы модели) и уровнем инфляции (выход модели), который оценивается через поквартальный индекс потребительских цен (ИПЦ). Модель будет использоваться для прогнозирования развития данного предприятия на будущие периоды времени (кварталы). Данные приведены в приложении.
Решение задачи прогнозирования нейронными сетями
Сценарий обработки данных примера приведен на рис. 2.1. Результаты факторного анализа приведены на рисунке 2.3.
Рисунок 3.1 – Сценарий Deductor
На третьем шаге создадим простую двухслойную сеть (с двумя скрытыми слоями) и архитектурой «2-4-1-1». Структура сети:
число слоев – 2;
число входов – 2;
число нейронов в первом скрытом слое – 4;
тип выходной функции первого слоя – tanh;
число нейронов во втором скрытом слое – 1;
тип выходной функции 2-ого слоя – linear.
При создании нейросети следует учитывать, что общее число связей сети (весов) должно быть в несколько раз меньше объема обучающей выборки. Это обеспечит достаточно гладкую аппроксимацию данных.
В противном случае нейросеть просто «переобучится», т.е. запомнит данные, потеряв возможность делать статистически значимые предсказания новых данных.
В нашем примере имеется 12 связей, а объем выборки – 32. Таким образом, необходимое условие успешного обучения формально выполняется, но для получения заведомо более качественного результата имеется 2 варианта - увеличение числа примеров до 150 (и более) или уменьшение числа связей до 3-5.
Первый путь реализуется легко введением достаточного числа дополнительных обучающих примеров. Второй вариант интереснее, и он может быть реализован разными способами. Например, уменьшением числа нейронов в промежуточном слое до 2. Тогда получится сеть типа «2-2-1» с пятью связями и т.д. Однако, продолжим работу с сетью «2-4-1-1».
Запустим процесс обучения сети. Точность обучения зададим 0.1, а число эпох 20000. Обучим сеть на 32 примерах, указав последние 4 примера как тестирующее множество.
На рис. 3.2 приведен граф нейронной сети, а на рис. 3.3 и 3.4 – результаты обучения и тестирования нейронной сети (график построен в MatLab).
В приведенных результатах ошибка обучения, а также ошибка на тестирующем множестве не так велика. Однако, это имеет место не всегда. Стоит попытаться обучить сеть несколько раз и проверить ее на тестирующем множестве, запоминая всякий раз лучший результат.
Рисунок 3.2 – Нейронная сеть, созданная программой Deductor
Рисунок 3.3 – Результаты обучения и тестирования нейронной сети
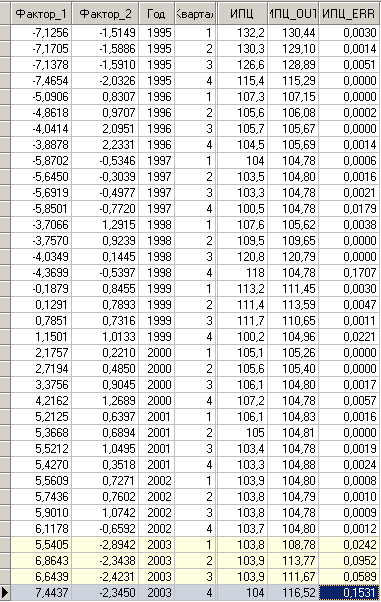
Рисунок 3.4 – Результаты обучения и тестирования нейронной сети
3.4 Задания к лабораторной работе
Задание 3.1. Для заданных исходных данных выполнить все этапы решения задачи прогнозирования с помощью нейронных сетей в системе MatLab:
Решение задачи разбейте на несколько этапов.
Предварительная обработка данных: нормировка и сокращение размерности методом главных компонент (в качестве входных параметров берем последние 7 из таблицы данных).
Построение нейронной сети на основе архитектуры многослойного персептрона.
Построение прогноза по обученной нейронной сети показателя ИПЦ на следующие 4 квартала на основе имеющихся экономических показателей предприятия, сравнение прогноза с известными показателями и оценка качества прогноза.
Задание 3.2. Сравнить результаты нейросетевого прогнозирования и прогнозирования с помощью линейной регрессионной модели.