
- •Возможные решения задач
- •8 Класс. Задача 1. Движение автомобилей.
- •Задача 2. Подъем тел.
- •Задача 3. Эксперимент по нагреванию воды.
- •Задача 4. Плавание льдины.
- •Xlvi Всероссийская олимпиада школьников по физике. Муниципальный этап. Возможные решения задач
- •9 Класс.
- •Xlvi Всероссийская олимпиада школьников по физике. Муниципальный этап. Возможные решения задач
- •10 Класс
- •Задача 1. Падение с отскоком.
- •Задача 2. Кресло на льду.
- •Xlvi Всероссийская олимпиада школьников по физике. Муниципальный этап. Возможные решения задач
- •11 Класс.
- •Задача 1. Движение по наклонной плоскости.
- •Задача 2 . Колебания грузика.
- •Задача 3. Растекание газа.
- •Задача 4. Движение электронов.
- •Задача 5. Выделение тепла в цепи.
Xlvi Всероссийская олимпиада школьников по физике. Муниципальный этап. Возможные решения задач
10 Класс
Задача 1. Падение с отскоком.
Первую часть полета тело преодолеет за время
![]() . (1)
. (1)
В момент отскока тело приобретает горизонтальную составляющую скорости, но зато полностью теряет вертикальную компоненту. С высоты h тело падает уже без начальной скорости. Таким образом, время падения на втором участке:
![]() . (2)
. (2)
Тогда общее время падения:
![]() . (3)
. (3)
Обозначим
![]() .
После возведения уравнения (3) в квадрат,
вычисление максимума функции (3) сводится
к нахождению максимального значения
квадратичной функции (подкоренного
выражения.):
.
После возведения уравнения (3) в квадрат,
вычисление максимума функции (3) сводится
к нахождению максимального значения
квадратичной функции (подкоренного
выражения.):
![]() , (4)
, (4)
которое, очевидно,
лежит ровно посередине между корнями
уравнения
![]() и
и
![]() .
Таким образом, получим искомый ответ
.
Таким образом, получим искомый ответ
![]() .
.
Критерии оценивания решения:
Обоснование потери вертикальной составляющей скорости
при отскоке - 2 балла.
Получение формулы для времени падения тела (3) - 4 балла.
Нахождение максимального значения функции (3)
и получение окончательного результата - 4 балла.
Задача 2. Кресло на льду.
Поскольку
кинетическая энергия кресла при ударе
не теряется, то для того, чтобы кресло
перевернулось, его кинетическая энергия
перед ударом о препятствие должна быть
не меньше
![]() ,
где
,
где
![]() и
и
![]() - высота центра тяжести кресла до и во
время переворачивания. Запишем закон
сохранения энергии:
- высота центра тяжести кресла до и во
время переворачивания. Запишем закон
сохранения энергии:
![]()
или расписывая слагаемые подробно:
![]() . (1)
. (1)
Выразим из формулы (1) начальную скорость кресла:
![]() . (2)
. (2)
Найдём далее
разность высот во время и до переворачивания.
Удобно рассматривать кресло в виде двух
тел – квадрата со стороной 0.5 м
и прямоугольника со сторонами 1
м и 0.1
м (см. рисунок
в условии задачи). Для расчета центра
тяжести кресла расположим начало
координат в правом нижнем углу фигуры.
Тогда координаты
![]() и
и
![]() центра масс определятся из следующих
формул:
центра масс определятся из следующих
формул:
![]() м2,
м2, ![]() м2, (3)
м2, (3)
где
![]() и
и
![]() - площади фигур. Тогда
- площади фигур. Тогда
![]() . (4)
. (4)
Конечная формула для расчета скорости принимает вид:
![]() м/с (5)
м/с (5)
Критерии оценивания решения:
Запись закона сохранения энергии (1) - 2 балла.
Получение расчетной формулы для начальной скорости кресла (2) - 2 балла.
Разбиение формы кресла на два тела и расчет точки центра масс (3) - 4 балла.
Получение численого результата для начальной скорости кресла (5) - 2 балла.
Задача 3. Как измерить длину нити маятника?
Прикрепим груз к веревке и подвесим получившийся маятник так, чтобы точки подвеса маятников находились примерно на одной вертикальной линии. Отклоним наш маятник и отпустим в момент, когда исходный маятник находится в точке максимального отклонения от положения равновесия. Таким образом, начальная фаза колебаний обоих маятников будет совпадать. Со временем маятник с меньшим периодом колебаний будет обгонять другой маятник по фазе. Однако, в какой-то момент колебания снова совпадут по фазе. Пусть, для определенности, маятником с большим периодом оказался маятник, который мы сделали сами. Очевидно, что к моменту повторного совпадения фаз первый маятник совершит N колебаний, а второй – на единицу меньше. Поэтому можем записать:
![]() , (1)
, (1)
где
![]() и
и
![]() - периоды колебаний исходного и второго
маятников. Из полученного выражения
видно, что, зная период тестового
маятников, а также число N
, которое определяется экспериментально,
можно определить период исходного
маятника. Используя формулу для
математического маятника, длина нити
исходного маятника может быть рассчитана
по следующей формуле:
- периоды колебаний исходного и второго
маятников. Из полученного выражения
видно, что, зная период тестового
маятников, а также число N
, которое определяется экспериментально,
можно определить период исходного
маятника. Используя формулу для
математического маятника, длина нити
исходного маятника может быть рассчитана
по следующей формуле:
![]() . (2)
. (2)
Здесь
![]() - длина нити второго маятника.
- длина нити второго маятника.
Критерии оценивания решения:
Идея сделать второй маятник и совместить начальные
фазы колебаний - 4 балла.
Получение соотношения периодов колебаний (1) - 4 балла.
Получение расчетной формулы (2) - 2 балла.
Задача 4. Опасный осколок.
Предположим, что порох сгорает полностью и происходит это достаточно быстро, чтобы пренебречь теплообменом между порохом и банкой. В этом случае можно полагать, что вся внутренняя энергия пороха переходит в механическую энергию осколков. Энергия, выделяющаяся при сгорании пороха, равна:
![]() , (1)
, (1)
где Q
– калорийность пороха. Энергия (1)
является источником для кинетической
энергии осколков банки. Считая, что
энергия равномерно распределяется по
поверхности банки, осколку массой
![]() достанется соответствующая часть
энергии. Скорость осколка в этом случае
можно оценить как
достанется соответствующая часть
энергии. Скорость осколка в этом случае
можно оценить как
![]() м/c (2)
м/c (2)
Данная оценка получена в предположении о мгновенном сгорании пороха, о полном сгорании пороха, об отсутствии теплообмена между порохом и банкой, о равномерном распределении кинетической энергии по поверхности стеклянной банки.
Критерии оценивания решения:
Запись формулы для энергии сгорания пороха - 2 балла.
Получение расчетной формулы и численного результата - 4 балла.
Обоснование сделанных допущений - 4 балла.
Задача 5. Чему равно сопротивление цепи?
Д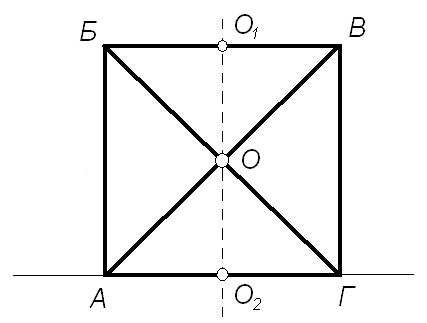
 ля
решения задачи необходимо найти точки
с одинаковым потенциалом. Эти точки
находятся на оси симметрии системы
(смотри рисунок, на котором ось обозначена
штриховой линией). Таким образом,
потенциалы точек О,
О1
и О2
равны друг другу. В соответсвии с правилом
эти точки с равными потенциалами могут
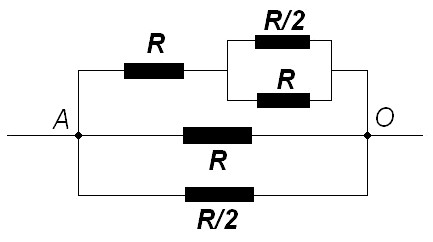
быть совмещены друг с другом. В результате
рассматриваемая комбинация разобьется
на два последовательно соединенных
одинаковых участка, один из которых
приведен на следующем рисунке.
Сопротивление такого участка определяется
уже без проблем:
ля
решения задачи необходимо найти точки
с одинаковым потенциалом. Эти точки
находятся на оси симметрии системы
(смотри рисунок, на котором ось обозначена
штриховой линией). Таким образом,
потенциалы точек О,
О1
и О2
равны друг другу. В соответсвии с правилом
эти точки с равными потенциалами могут
быть совмещены друг с другом. В результате
рассматриваемая комбинация разобьется
на два последовательно соединенных
одинаковых участка, один из которых
приведен на следующем рисунке.
Сопротивление такого участка определяется
уже без проблем:
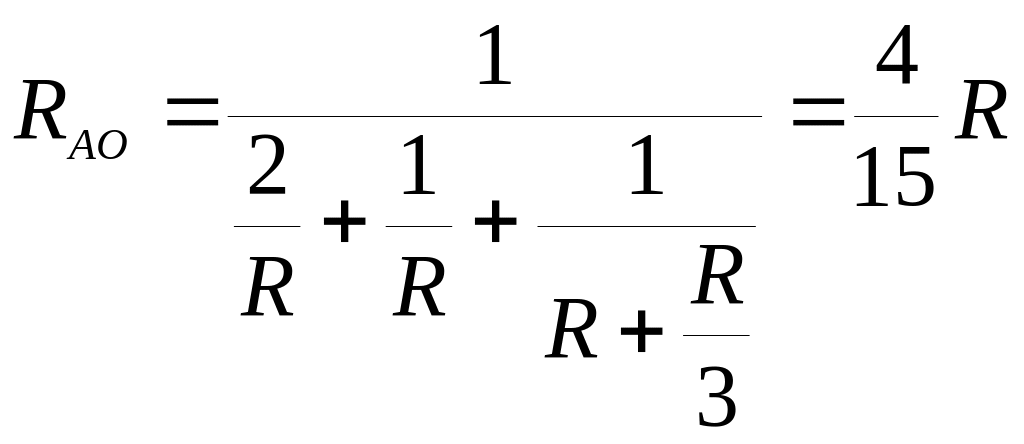 (1)
(1)
Таким образом, искомое сопротивление всего квадрата есть
![]() (2)
(2)
Критерии оценивания решения:
Построение эквивалентной схемы - 6 баллов.
Получение расчетной формулы (1) - 2 балла.
Получение численного результата (2) - 2 балла.
