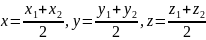- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота № 1 Властивості визначників. Обчислення визначників за допомогою їх властивостей.
- •Вправи для самостійної роботи
- •Індивідуальні завдання №1
- •Самостійна робота № 2 Ранг матриці та способи його обчислення.
- •Приклади розв’язання типових задач.
- •Самостійна робота № 3 Обернена матриця
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання №3
- •Самостійна робота № 4
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 4
- •Самостійна робота № 5
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 5
- •Самостійна робота № 6
- •Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 6
- •Самостійна робота № 7 вектори
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота № 8
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 7
- •Індивідуальні завдання №8
- •Основні теоретичні відомості
- •Приклади розв’язання типових задач.
Вправи для аудиторної роботи.
1. Розв’яжіть системи рівнянь методом Гаусса:
1)
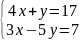 .
2)
.
2)
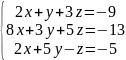 .
.
3)
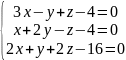 .
4)
.
4)
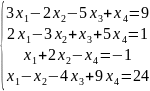 .
.
5)
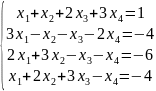 .
6)
.
6)
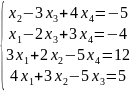 .
.
Індивідуальні завдання № 6
7.1. Розв’яжіть систему лінійних рівнянь методом Гаусса:
1) . 2) .
3) . 4) .
5) . 6) .
7) . 8) .
9) . 10) .
11) . 12) .
13) . 14) .
15) . 16)
17) . 18) .
19) . 20) .
21) . 22)
23) . 24) .
25) .
Самостійна робота № 7 вектори
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Векторна величина на відміну від скалярної задається не лише своїм чисельним значенням, а й напрямом (швидкість, прискорення, сила та ін.).
Геометрично
вектор являє собою напрямлений
відрізок і позначається
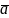 ,
або
,
або
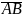 ,
де точка А – початок вектора, а В – його
кінець.
,
де точка А – початок вектора, а В – його
кінець.

Рис.1
Відстань
між початком вектора і його кінцем
називають довжиною
(або модулем)
вектора і позначають
 ,
або
,
або
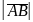 .
.
Вектори, які лежать на одній прямій або паралельних прямих, називають колінеарними.
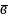
Рис.2
В ектори і рівні, якщо вони колінеарні, мають однакові модулі і однакові напрями.
Рис.3
Два вектори називають протилежними, якщо вони колінеарні, мають однакові модулі і протилежні напрями.
Рис.4
Вектор, початок і кінець якого збігаються, називають нуль-вектором. Напрям його не визначений.
Вектор, довжина якого дорівнює одиниці, називають одиничним вектором.
Одиничний
вектор, напрям якого збігається з
напрямом вектора
,
називають ортом вектора
і позначають
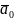 .
.
Вектори можна вільно переміщувати по площині (у просторі). Тому в аналітичній геометрії їх називають вільними.
Кутом між векторами і , зведеними до спільного початку, називають найменший кут, на який треба повернути вектор навколо спільного початку, щоб він збігся з вектором .
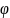
Рис.5
Три вектори називають компланарними, якщо вони лежать в одній або паралельних площинах.
Зокрема, три вектори компланарні, якщо два з них або всі три колінеарні, або хоча б один з них – нуль-вектор.
Лінійні операції над векторами.
До лінійних операцій над векторами належать:
1) додавання (віднімання) векторів;
2) множення вектора на число (скаляр).
Сумою
векторів
і
називають вектор
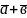 ,
який сполучає початок вектора
з кінцем вектора
за умови, що вектор
прикладений до кінця вектора
.
,
який сполучає початок вектора
з кінцем вектора
за умови, що вектор
прикладений до кінця вектора
.
правило
трикутника Рис.6
Суму двох векторів можна будувати також за правилом паралелограма.
Рис.7
Віднімання векторів визначається як дія, обернена додаванню.
Різницею
векторів
і
називають вектор
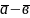 ,
який у сумі з вектором
складає вектор
,
або, іншими словами, це вектор, що сполучає
кінець вектора
з кінцем вектора
за умови, що
і
прикладені до спільного початку.
,
який у сумі з вектором
складає вектор
,
або, іншими словами, це вектор, що сполучає
кінець вектора
з кінцем вектора
за умови, що
і
прикладені до спільного початку.
Рис.8
Добутком
вектора
на скаляр
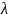 називають вектор
називають вектор
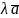 такий, що
такий, що
 =
=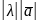 і напрям якого збігається з напрямом
вектора
,
якщо
і напрям якого збігається з напрямом
вектора
,
якщо
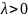 ,
або протилежний до напряму вектора
,
якщо
,
або протилежний до напряму вектора
,
якщо
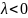 .
Так на рис.9 зображено вектори
,
4
,
-2
.
.
Так на рис.9 зображено вектори
,
4
,
-2
.
Рис.9 4 -2
З означення множення вектора на число випливає, що коли вектори колінеарні, то існує єдине число таке, що = , і навпаки, якщо = , то
і колінеарні.
Сформулюємо властивості лінійних операцій над векторами:
1.
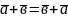 .
.
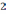 .
.
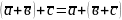 .
.
3.
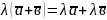 .
.
4.
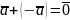 .
.
5.
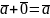 .
.
6.
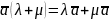 .
.
7.
 .
.
Проекція вектора на вісь.
Віссю називають напрямлену пряму, на якій вибрано початок відліку, додатний напрям і одиницю довжини.
Проекцією точки А на вісь l називають основу перпендикуляра АА1 (точка А1), опущеного з точки А на вісь l (рис.10).
В В
А Рис.10 А Рис.11
 А1
В1
l
В1
А1
l
А1
В1
l
В1
А1
l
Нехай
задано вісь l
і вектор
.
Позначимо через А1
та В1
проекції на вісь l
відповідно початку А і кінця В вектора
і розглянемо вектор
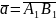 .
.
Проекцією
вектора
на вісь l називають
додатне число
 ,
якщо вісь l
і вектор
,
якщо вісь l
і вектор
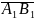 однаково напрямлені (рис.10), і від’ємне
число
однаково напрямлені (рис.10), і від’ємне
число
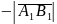 ,
якщо вісь l
і вектор
протилежно напрямлені (рис.11).
,
якщо вісь l
і вектор
протилежно напрямлені (рис.11).
Проекцією
вектора
на вісь l
позначають так:
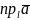 (або
(або
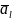 ).
).
Кутом
між вектором
і віссю l називають
менший з кутів, на який треба повернути
вектор
або вісь l,
щоб він збігався за напрямом з другим
вектором або віссю. Цей кут міститься
у межах від 0 до
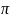 .
.
Проекцію вектора на вісь l обчислюють за формулою
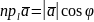
де - кут між напрямом осі l і напрямом вектора .
При
цьому
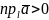 ,
якщо кут
-
гострий,
,
якщо кут
-
гострий,
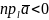 ,
якщо кут
-
тупий,
,
якщо кут
-
тупий,
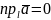 ,
якщо
,
якщо
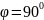 .
.
Сформулюємо деякі властивості проекцій.
1. Проекція суми кількох векторів на ту саму вісь дорівнює сумі їх проекцій на цю вісь, тобто
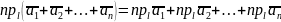 .
.
2. При множенні вектора на число його проекція також помножиться на це число:
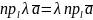 .
.
Лінійна залежність і незалежність векторів. Базис.
Застосовуючи лінійні операції над векторами, можна знаходити вирази вигляду
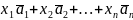 ,
,
Які
називають лінійними
комбінаціями векторів
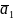 ,
,
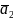 ,…,
,…,
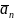 ;
числа
,
;
числа
,
,…, - коефіцієнти.
Вектори
,
,…,
називають лінійно
залежними, якщо існують
такі числа
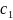 ,
,
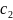 ,…,
,…,
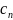 не всі рівні нулю, що лінійна комбінація
не всі рівні нулю, що лінійна комбінація
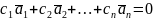 ,
,
і лінійно незалежними, якщо ця рівність виконується лише за умови, коли всі числа , ,…, рівні нулю.
Сукупність
лінійно незалежних векторів
,
,…,
називають базисом
простору
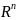 ,
якщо для кожного вектора з
існують такі дійсні числа
,
,
якщо для кожного вектора з
існують такі дійсні числа
,
,…, , що виконується рівність
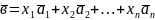 .
.
Цю рівність називають розкладом вектора у базисі , ,…, .
Базисом на прямій називають довільний ненульовий вектор на цій прямій.
Якщо
вектор
- базис, то існує єдиний розклад вектора
:
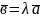 ,
де
- координата вектора
за базисом
.
,
де
- координата вектора
за базисом
.
Базисом на площині називають довільну упорядковану пару неколінеарних векторів.
Базисом у просторі називають довільну упорядковану трійку некомпланарних векторів.
Якщо
вектори
та
- базис на площині і
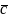 - довільний ненульовий вектор площини,
то існують сталі
- довільний ненульовий вектор площини,
то існують сталі
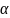 та
та
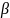 такі, що
такі, що
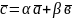 (рис.12)
(рис.12)
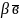 Рис.12
Рис.12
Коефіцієнти , називають координатами вектора в даному базисі.
Якщо
вектори
,
і
- базис у просторі і вектор
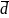 розкладений за базисом, тобто
розкладений за базисом, тобто
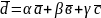 ,
то числа
,
то числа
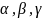 називають координатами вектора
в даному базисі.
називають координатами вектора
в даному базисі.
Таким чином, базис у просторі дає змогу кожний вектор одночасно зіставити з упорядкованою трійкою чисел (координатами цього вектора) і, навпаки, кожну упорядковану трійку чисел за допомогою базису можна зіставити з єдиним вектором
.
Координати вектора. Дії над векторами.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Точку
О й упорядковану трійку некомпланарних
векторів
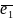 ,
,
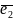 ,
,
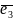 (базису) називають декартовою
системою координат у просторі.
(базису) називають декартовою
системою координат у просторі.
Точка О – початок координат, а осі, які проходять через початок координат у напрямі базисних векторів, називають осями координат.
Упорядковану
трійку одиничних попарно ортогональних
векторів
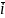 ,
,
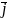 ,
,
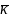 (
(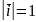 ,
,
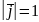 ,
,
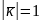 )
називають ортонормованим
базисом.
)
називають ортонормованим
базисом.
Прямокутною
декартовою системою координат (ПДСК) у
просторі називають декартову систему,
базис якої ортонормований, і позначають
її через
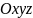 (
(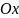 - вісь абсцис,
- вісь абсцис,
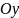 - вісь ординат,
- вісь ординат,
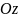 - вісь аплікат (рис.1)).
- вісь аплікат (рис.1)).
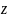
М3
М
М2
О
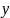
Рис.1
 М1
М0
М1
М0
Розклад вектора за ортами координатних осей.
Нехай
- довільний ненульовий вектор простору,
сумістимо його початок з початком
координат:
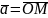 (рис.1).
(рис.1).
Проведемо
через точку М площини, паралельні
координатним площинам. Точки перетину
цих площин з осями координат позначимо
через М1,
М2 та
М3.
Дістанемо прямокутний паралелепіпед,
однією з діагоналей якого є вектор
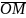 .
Тоді
.
Тоді
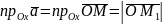 ,
,
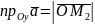 ,
,
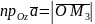 .
.
Позначимо
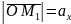 ,
,
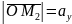 ,
,
 .
.
Враховуючи векторні рівності
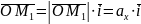 ,
,
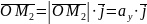 ,
,
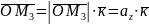 ,
,
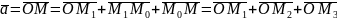 ,
,
дістанемо
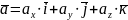 (1)
(1)
Ця формула є основною у векторній алгебрі і називається розкладом вектора за ортонормованим базисом , , .
Векторну рівність (1) у символічній формі ще записують так:
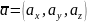 ,
або
,
або
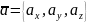 .
.
Довжина вектора. Напрямні косинуси.
Довжину (модуль) вектора обчислюють за формулою
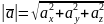
Ця формула безпосередньо випливає з того факту, що квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів його ребер.
Оскільки
координати вектора
- це проекції вектора
на координатні осі, то
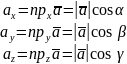
д
е
,
,
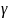 - кути, які вектор
утворює з осями координат
,
,
відповідно (рис.2)
- кути, які вектор
утворює з осями координат
,
,
відповідно (рис.2)
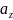

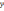
Рис.2
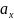
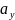
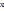
Тоді
 (2)
(2)
Косинуси
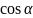 ,
,
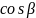 ,
,
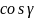 кутів
,
,
називають напрямними
косинусами
вектора
;
вони визначають напрям вектора
в системі
і задовольняють рівність
кутів
,
,
називають напрямними
косинусами
вектора
;
вони визначають напрям вектора
в системі
і задовольняють рівність
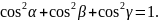
Звідси випливає, що орт вектора має вигляд
 ,
,
де напрямні косинуси визначають за формулою (2).
Дії над векторами.
Нехай вектори задані своїми координатами, тобто
,
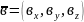 ,
,
тоді
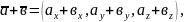

Іншими словами, при додаванні векторів їхні відповідні координати додають; при множенні вектора на скаляр координати вектора множать на цей скаляр.
Вектори і рівні тоді і тільки тоді, коли рівні їхні відповідні координати:
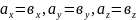 .
.
Колінеарність векторів.
З’ясуємо
умови колінеарності векторів
і
,
заданих своїми координатами. Нехай
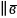 ,
тоді
=
,
де
,
тоді
=
,
де
 - деяке число. Тоді
- деяке число. Тоді
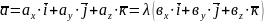 .
.
Звідси
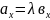 ,
,
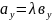 ,
,
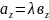
тобто
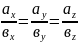 (3)
(3)
Отже, координати колінеарних векторів пропорційні. І навпаки, якщо координати двох векторів пропорційні, то ці вектори колінеарні.
Координати точки.
Довільній
точці М простору можна зіставити у ПДСК
вектор
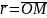 ,
який називають радіус-вектором точки
М. Тоді існує єдина трійка чисел (х, у,
z) така, що
,
який називають радіус-вектором точки
М. Тоді існує єдина трійка чисел (х, у,
z) така, що
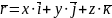 .
.
Координати х, у, z радіус-вектора називають координатами точки М і пишуть М(х, у, z).
Якщо
відомі координати початку
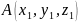 та кінця
та кінця
 вектора
,
то його координати знаходять за формулою
вектора
,
то його координати знаходять за формулою

Довжину вектора (або відстань між точками А та В) записують так:
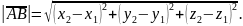
Поділ відрізка у даному відношенні.
Нехай
задано відрізок
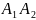 точками
точками
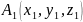 і
і
 .
Тоді координати точки
М(х, у, z), яка ділить
цей відрізок у відношенні
,
тобто
.
Тоді координати точки
М(х, у, z), яка ділить
цей відрізок у відношенні
,
тобто
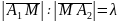 ,
знаходять за формулами
,
знаходять за формулами
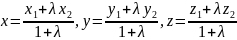 (4)
(4)
Зокрема,
координати точки, яка ділить відрізок
навпіл (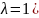 ,
такі:
,
такі: