
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота № 1 Властивості визначників. Обчислення визначників за допомогою їх властивостей.
- •Вправи для самостійної роботи
- •Індивідуальні завдання №1
- •Самостійна робота № 2 Ранг матриці та способи його обчислення.
- •Приклади розв’язання типових задач.
- •Самостійна робота № 3 Обернена матриця
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання №3
- •Самостійна робота № 4
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 4
- •Самостійна робота № 5
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 5
- •Самостійна робота № 6
- •Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 6
- •Самостійна робота № 7 вектори
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота № 8
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 7
- •Індивідуальні завдання №8
- •Основні теоретичні відомості
- •Приклади розв’язання типових задач.
Приклади розв’язання типових задач.
Користуючись методом Крамера, розв’язати систему рівнянь:
1.

Розв'язання. Обчислимо визначник системи
 .
.
Оскільки
 ,
то задана система рівнянь сумісна і має
єдиний розв’язок. Обчислимо визначники
,
то задана система рівнянь сумісна і має
єдиний розв’язок. Обчислимо визначники
 ;
;
 ;
;
 .
.
Значить, за формулами Крамера
 ;
;
 ;
;
 .
.
Таким
чином,
 ,
,
 ,
,
 - єдиний розв’язок системи.
- єдиний розв’язок системи.
2.

Розв'язання. Основна матриця системи має вигляд
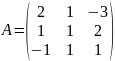
Використовуючи властивості визначників, обчислюємо визначник основної матриці:


Використаємо тепер формули Крамера:
 ,
,
 ,
,
 ;
;
 ,
,
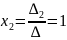 ,
,
 .
.
Зауваження.
Визначник
 можна не обчислювати, оскільки, знаючи
та
,
невідоме
можна не обчислювати, оскільки, знаючи
та
,
невідоме
 можна визначити з будь-якого рівняння
системи після підстановки в нього
значень
та
.
можна визначити з будь-якого рівняння
системи після підстановки в нього
значень
та
.
Вправи для аудиторної роботи.
Розв’яжіть системи рівнянь методом Крамера:
1)
 .
2)
.
2)
 .
3)
.
3)
 .
.
4)
 .
5)
.
5)
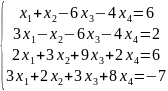 .
.
6)
 .
7)
.
7)

Індивідуальні завдання № 4
1. Розв’яжіть систему лінійних рівнянь за формулами Крамера:
1)
 .
2)
.
2)
 .
.
3)
 .
4)
.
4)
 .
.
5)
 .
6)
.
6)
 .
.
7)
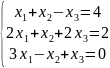 .
8)
.
8)
 .
.
9)
 .
10)
.
10)
 .
.
11)
 .
12)
.
12)
 .
.
13)
 .
14)
.
14)
 .
.
15)
 .
16)
.
16)
 .
.
17)
 .
18)
.
18)
 .
.
19)
 .
20)
.
20)
 .
.
21)
 .
22)
.
22)
 .
.
23)
 .
24)
.
24)

25)
 .
.
---------------------------------------------------------------------------------------------------
Самостійна робота № 5
Розв’язання систем лінійних алгебраїчних рівнянь матричним методом.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Розглянемо систему n лінійних рівнянь з n невідомими:
(1)
Позначимо через А матрицю, складену із коефіцієнтів при невідомих (так звану основну матрицю системи); Х – матрицю-стовпець із невідомих; В – матрицю-стовпець із вільних елементів, тобто
,
 ,
,
 .
(2)
.
(2)
Тоді систему рівнянь (1) можна переписати у вигляді матричного рівняння: . Його розв’язок Х=А-1В називається матричним розв’язком системи лінійних рівнянь з n невідомими. Знаходження матричного розв’язку називається матричним способом розв’язування системи лінійних рівнянь.
Приклади розв’язання типових задач.
1. Записати і розв’язати в матричній формі систему рівнянь

Розв'язання.
Позначимо через
 ,
,
 ,
,
 .
.
Система лінійних рівнянь запишеться у матричній формі . Матричний розв’язок системи буде Х=А-1В.
Для знаходження оберненої матриці А-1 обчислимо визначник

Оскільки , то для матриці А існує обернена А-1 , а значить, можна знайти єдиний розв’язок вихідної системи.
Знаходимо алгебраїчні доповнення:
 ,
,
 ,
,
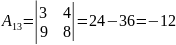 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Отже,
 .
Транспонуємо
.
Транспонуємо
 ,
тоді
,
тоді
 .
.
Обернена матриця має вигляд:
 .
.
Перевіряємо:
 =
=
=
 .
.
Обернену матрицю знайдено правильно.
Знаходимо розв’язок заданої системи:
Х=А-1В= .
.
Розв’язок
системи лінійних рівнянь:
,
 ,
,
 .
.
