Расчет электрических цепей переменного тока
2.1 Общие положения
Для расчета электрических цепей переменного тока применяются те же методы, что и для цепей постоянного тока, но т.к. переменный синусоидальный ток характеризуется большим количеством параметров и его аналитическое представление сложнее, то это вносит свои особенности в методику расчета.
Наиболее удобной для расчетов является комплексная форма представления синусоидальных функций.
Основные закономерности, необходимые для расчета эл. цепей переменного тока (комплексная форма)
закон Ома для участка эл. цепи, с полным комплексным сопротивлением |
1-ый закон Кирхгофа |
2-ой закон Кирхгофа |
|
|
|
Сила тока на участке цепи прямо пропорциональна напряжению участка и обратно пропорциональна его сопротивлению. |
Алгебраическая сумма токов в узле электрической цепи равна нулю. |
Алгебраическая сумма падений напряжения в контуре электрической цепи равна алгебраической сумме ЭДС в нем. |
Далее рассмотрим расчет электрической цепи переменного тока с одним источником методом эквивалентного преобразования схемы. Данный метод содержит общую для всех методик подготовительную часть и в тоже время имеет свою специфику.
2.2 Методика расчета электрической цепи с одним источником эдс путем эквивалентного преобразования схемы.
2.2.1 Подписать узлы, расставить произвольно направления токов в ветвях и подписать токи.
2.2.2 Найти сопротивления всех реактивных потребителей в цепи по формулам:
,
.
2.2.3 Определить полное комплексное сопротивление цепи относительно зажимов источника, для чего используем выражения:
– для
последовательного соединения;
– для
параллельного соединения;
– при
параллельном соединении двух потребителей.
Если необходимо выполнить преобразование звезда-треугольник (рис. 2.1 и 2.2)
,
,
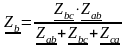– для преобразования треугольника в
звезду;
,
,
– для преобразования звезды в треугольник.
2.2.4 Вычислить ток на входе по закону Ома .
2.2.5 Поэтапно используя закон Ома для отдельных участков, а также законы Кирхгофа для узлов и контуров «разворачиваем» схему и находим токи внутренних ветвей.
2.2.6 Проверку выполняют либо по балансу мощностей, либо построением векторной диаграммы в масштабе.
Пример расчета электрической цепи с одним источником ЭДС методом эквивалентного преобразования схемы |
задание |
З Дано: U=100 В, R1=5 Ом, R2=8 Ом, L1= 31,8 мГн, L2= 15,9 мГн, C1= 159 мкФ, C2= 318 мкФ, f = 50 Гц.
Требуется:
|
выполняем п. 2.2.1 |
Т.к. в цепи все элементы включены последовательно (измерительные приборы не учитываем), то протекает один ток.
|
выполняем п. 2.2.2 |
Находим сопротивления реактивных элементов
|
выполняем п. 2.2.3 |
П
Запишем
сопротивления элементов в комплексной
форме:
|
выполняем п. 2.2.4 |
Определим
ток на входе цепи
|
выполняем п. 2.2.5 |
Найдем напряжения на участках:
|
выполняем п. 2.2.6 |
П Из векторной диаграммы следует, что второй закон Кирхгофа для рассчитанной цепи выполняется. Кроме того, фазовые сдвиги на элементах соответствуют установленным правилам. Следовательно, расчет тока и напряжений выполнен верно.
|
Пункты 2.2.1-2.2.6 соответствуют п. «а» и «б» задания. Выполним п. «в» и «г». Рассчитаем активную, реактивную и полную мощность на входе цепи одним из двух способов:
Пример расчета в комплексной форме:
|
Измерительные приборы на переменном токе, как правило, определяют действующие значения. Амперметр
измеряет действующее значение входного
тока
|
адана
схема цепи однофазного приемника
переменного тока, представляющая
последовательное соединение активных,
индуктивных и емкостных элементов.
Ом,
Ом,
Ом,
Ом.
олное
комплексное сопротивление цепи
относительно зажимов источника
.
,
– активные;
,
– индуктивные;
,
– емкостные.
Ом.
.
Здесь возможны два варианта вычисления:
А;
А.
В,
В,
В,
В,
В,
В.
остроим
векторную диаграмму в масштабе.
Масштабы выбираются после анализа
рассчитанных величин токов и напряжений.
Масштаб тока принимаем mi=1А/см,
масштаб напряжения принимаем mu=20В/см.
При построении векторной диаграммы
необходимо наглядно подтвердить
выполнение законов Кирхгофа. Для
рассматриваемой цепи справедлив 2-ой
закон Кирхгофа
.
,
где
-
сопряженный комплекс тока;
,
Вт;
,
ВАР;
,
ВА, где φ – фазовый сдвиг между током
и напряжением.
ВА,
где Р = 330 Вт, Q = -381 ВАР,
503
ВА.
А.
Вольтметр измеряет действующее
значение напряжения на участке 3-4-5
заданной цепи. Найдем комплексное
напряжение на участке 3-4-5:
В,
откуда
В.