Решение

2.1. Для силовых трехфазных трансформаторов можно считать, что практически равна вторичной, поскольку номинальное значение КПД близко к единице. Поэтому номинальные линейные значения первичного и вторичного токов трансформатора определяем из этих соотношений:

А

А

Значения фазных токов и напряжений определяем на основе известных из курса ТОЭ соотношений между линейными и фазными величинами в трехфазной системе при соединении обмоток трансформатора в Y:

кВ

А

кВ

А

Величину тока холостого хода в амперах определяем из соотношения

А.

2.2. Для определения параметров схемы замещения трансформатора вначале находим значение фазного напряжения короткого замыкания, а также величину полного, активного и индуктивного сопротивлений короткого замыкания по следующим зависимостям

кВ

Ом

Ом

Ом

Поскольку и, то сопротивления обмоток трансформатора можно легко определить на основе допущения, чтои, то есть

Ом и Ом

Значение величин полного, активного и индуктивного сопротивлений ветви намагничивания для схемы замещения трансформатора определяем из соотношений

кОм

кОм

кОм

На основе выполненных расчетов вычерчиваем Т-образную схему замещения трансформатора и указываем на ней величины соответствующих сопротивлений (рис. 4).

Х_K=67 Ом

r_K=32 Ом

r₀=8.8 кОм

Х₀=57 кОм

Рис. 4. Схема замещения трансформатора.

2.3. Оптимальный коэффициент загрузки трансформатора по току, соответствующий максимальному КПД, определяем из соотношения . Величину КПД трансформатора при заданном значении загрузки по току определяем методом отдельных потерь по формуле

.

Для построения зависимости в выражение КПД подставляем значения_i=0; 0.25; 0.5; 0.75; 1; 1.25 и находим соответствующие им значения . По полученным данным строим график (рис. 5).

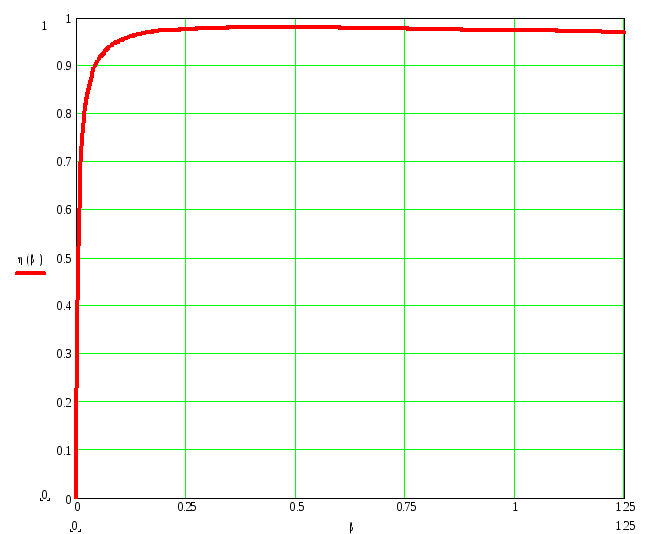
Рис. 5. Зависимость КПД трансформатора от нагрузки.

2.4. Для построения зависимости воспользуемся выражением

, где

,

В выражение для подставляем значения_i=0; 0.25; 0.5; 0.75; 1; 1.25 и находим соответствующие им величины . На основании полученных данных строим график (рис. 6).

Для построения внешней характеристики трансформатора находим значение вторичного напряженияпри рассматриваемых выше значениях_i, то есть . На основании полученных данных строим график (рис. 6).

U%, U₂%

100

U₂%

U%



Рис 6. Зависимость изменения вторичного напряжения от изменения нагрузки и внешняя характеристика трансформатора

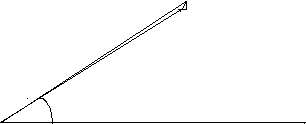
2.5. Упрощенную векторную диаграмму трансформатора строим следующим образом. На листе бумаги строим горизонтально вектор номинального вторичного тока в произвольном масштабе. Под углом в сторону опережения от строим вектор вторичного номинального напряжениядлиной 100 мм (отрезок ОА). С конца векторапараллельно векторустроим вектор, по модулю равный(отрезок АВ). От точки В перпендикулярно к векторуоткладываем вектор, по модулю равный, и получаем точку С. Соединив точки А и С, получаем прямоугольный треугольник короткого замыкания трансформатора. Отрезок СО характеризует величину подведенного к трансформатору напряжения(рис. 7).

С

АВ

₂

О

Рис. 7. Упрощенная векторная диаграмма трансформатора.

Задача 3. Для однофазного асинхронного микродвигателя с пусковым активным сопротивлением и с пусковой емкостью выполнить следующее:

3.1. Описать устройство и принцип действия микродвигателя с использованием конструктивных схем, разрезов; электрических схем устройства и управления; векторных диаграмм.

3.2. Нарисовать график механической характеристики микродвигателя.

3.3. Описать особенности, достоинства и недостатки микромашин и области их применения.