Вопрос №5

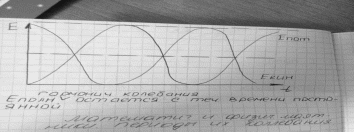
Вопрос №6 Энергия простого гармонического движения

Кинетическая энергия K системы в зависимости от времени t такова:

и потенциальная энергия есть

Полная механическая энергия системы, однако, имеет постоянное значение

Вопрос №9

Колебания, энергия которых уменьшается с течением времени за счет действия сил сопротивления, называются затухающими.

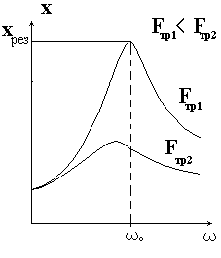
Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний называется резонансом.

Условие резонанса: w₀ = w_вын = w_рез, х - увеличивается.

Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различного вида сооружениях. Используется в акустике, радиотехнике и т.д.

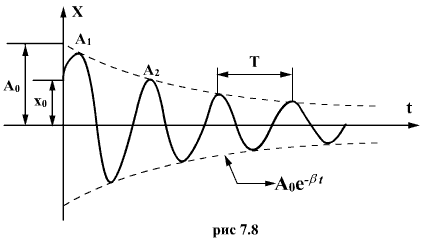
График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

Натуральный логарифм отношения амплитуд смещений, следующих друг за другом через промежуток времени, равный периоду Т, называют логарифмическим декрементом затухания.

Обозначим через τ промежуток времени, за который амплитуда колебаний уменьшается в е раз. Тогда

откуда

Следовательно, коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

Пусть N - число колебаний, после которых амплитуда уменьшается в е раз, Тогда

Следовательно, логарифмический декремент затухания δ есть физическая величина, обратная числу колебаний N, по истечению которого амплитуда убывает в е раз

Вопрос 11

Продольные волны ─ распространяющееся с конечной скоростью в пространстве переменное взаимодействие материи, которое обычно характеризуется двумя функциями ─ векторной, направленной вдоль потока энергии волны, и скалярной функцией. В упругих волнах (звуковых волнах) векторная функция описывает колебания скорости движения элементов среды распространения волны. В зависимости от вида продольных волн и среды их распространения, скалярная функция описывает разного рода изменения в среде или в поле, например, плотность вещества.

ПОПЕРЕЧНАЯ ВОЛНА - волна, у которой характеризующая её векторная величина лежит в плоскости, перпендикулярной направлению распространения волны (для гармонических волн - волновому вектору ). К П. в. относят, напр., волны в струнах или упругих мембранах, когда смещения частиц в них происходят строго перпендикулярно направлению распространения волн, а также плоские однородные электромагнитные волны в изотропном диэлектрике или магнетике; в этом случае поперечные колебания совершают векторы электрических и магнитных полей.

Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде с некоторой скоростью v. Процесс распространения колебаний называется волной. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебания частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн. В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.

Распространение волн в упругой среде.

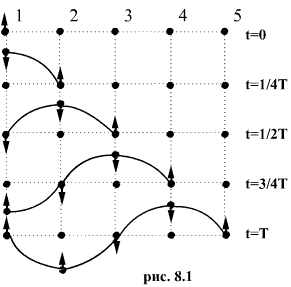
На рис.8.1 показано движение частиц при распространении в среде поперечной волны. Номерами 1,2,3 и т.д. обозначены частицы, отстоящие друг от друга на расстоянии, равном , т.е. на расстоянии, проходимом волной за четверть периода колебаний, совершаемых частицами. В начальный момент времени (t = 0) все точки расположены на прямой и ни одна из них не выходит из положения равновесия. Приведем точку 1 в гармоническое колебание с периодом Т, направленное перпендикулярно линии 1-5. Гак как частицы среды связаны между собой силами упругости, они тоже приходят в колебания, но с некоторым запаздыванием. Через четверть периода точка 1 отклонится от линии равновесия на максимальное смещение. Колебание начали все точки, лежащие слева от точки 2. По истечении времени начнет подниматься вверх и точка 2. При , первая точка вернется в положение равновесия, вторая точка достигнет максимального отклонения, и колебания дойдут до точки 3. При точка 1 достигнет максимального отрицательного смещения, точка 2 вернется в положение равновесия и колебания достигнут точки 4. Наконец, за время, равное периоду t = Т, точка 1 вернется в положение равновесия, совершив полностью одно колебание. Колебания распространились до точки 5, все колеблющиеся точки образуют волну. При дальнейших колебаниях точек волновой процесс распространится вправо от точки 5. В рассмотренном случае образования поперечной волны каждая частица движется только вверх и вниз. У наблюдателя же создается впечатление, что «волна бежит», хотя в действительности происходит только передача движения от одной точки среды к другой.

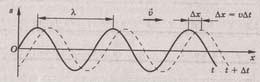
В момент времени равный периоду (t = Т), точки 1 и 5, находящиеся в положении равновесия, имеют одинаковое смещение и одинаковое направление движения (вверх). Поэтому говорят, что точки I и 5 имеют одинаковые фазы. В отличие от этого точки 1 и 3, хотя смещения у них одинаковы, движутся в противоположные стороны, поэтому говорят, что точки 1 и 3 находятся в противоположных фазах. Расстояния между точками 1 и 5 определяет длину волны λ т.е. длиной волны λ называется, расстояние между ближайшими точками волны, колеблющимися в одинаковых фазах. Периодом волны Т называют время одного полного колебания ее точек. Величина, обратная периоду, называется частотой волны. Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой: Так как то,

(8.1)

Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле: , а поперечной:

где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.

Вопрос №12

Волны называются поперечными, если частицы среды колеблются перпендикулярно (поперек) лучу волны. Они существуют в основном за счет сил упругости, возникающих при деформации сдвига, а поэтому существуют только в твердых средах.

На поверхности воды возникают поперечные волны, так как колеблется граница сред.

В поперечных волнах различают горбы и впадины.

Длина поперечной волны - расстояние между двумя ближайшими горбами или впадинами.