1.2.2. Силы

Если на частицу в пространстве воздействуют другие тела, то частица находится в поле сил.

Поле сил является однородным, если во всех точках поля силы, действующие на частицу, одинаковы по величине и направлению, т.е. = const.

Поле сил является центральным, если направление силы, действующей на частицу, в любой точке пространства проходит через неподвижный центр, а величина силы зависит только от расстояния до этого центра, т.е. F = F(r).

При этом поля сил одной природы могут быть в одних случаях однородными, в других центральными, в зависимости от условий рассмотрения. Например, рассматривая движение тела вблизи поверхности Земли, поле силы тяжести можно считать однородном; рассматривая движение тела, движущегося на орбите Земли, поле силы гравитационного взаимодействия – центральное.

1.2.2.3. Силы трения

Силы трения действуют между соприкасающимися телами или их частями, как при их относительном движении, так и при их относительном покое. Силы трения направлены по касательной к поверхности соприкосновения противоположно скорости данного тела.

В результате действия сил трения происходит превращении механической энергии во внутреннюю энергию соприкасающихся тел.

Силы внутреннего трения возникают при перемещении частей одного и того же тела относительно друг друга, наиболее часто возникают при движении жидкостей и газов и будет рассмотрены в разделе «Молекулярная физика».

Сила внешнего трения возникают при соприкосновении различных тел

Различают несколько видов внешнего трения: трение скольжения и трение качения.

Сила трения скольжения

F = k_с N,

где k_с – коэффициент трения скольжения, зависящий от материала соприка–сающихся поверхностей и от состояния этих поверхностей; N – сила реакции опоры.

Сила трения качения

F = k_к ,

где k_к – коэффициент трения качения, зависящий от материала соприкасающихся поверхностей; N – сила реакции опоры; R – радиус катящегося тела.

1.2.2.4. Упругие силы

При действии на тело сил оно деформируется. Если после прекращения действия силы тело полностью восстанавливает форму и размер, то такая деформация называется упругой. Различают несколько видов деформаций: растяжение или сжатие, кручение, сдвиг, изгиб.

Для характеристики деформации тел введем понятие напряжение , численно равное упругой силе d _упр, приходящейся на единицу площади dS сечения тела

 = .

Р.Гук экспериментально установил, что напряжение упруго деформированного тела пропорционально его относительной деформации

 = æ ,

где æ – модуль упругости, зависит от свойств материала.

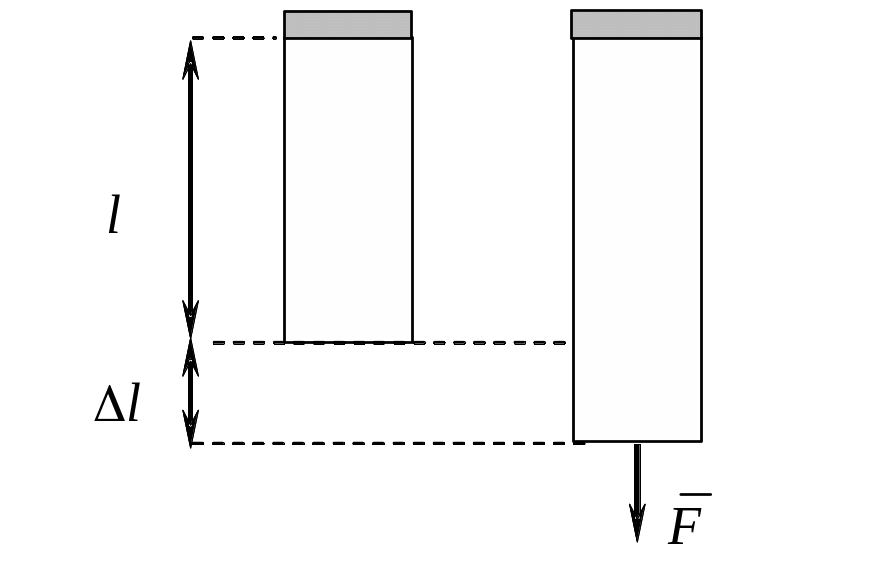
Деформация растяжения

Учитывая, что напряжение, возникающее при деформации тела

 = и  = ,

получим

F_упр = E S ,

где Е – модуль растяжения (модуль Юнга), – относительное растяжение.

Учитывая, что модуль растяжения E, площадь поперечного сечения тела S, исходная длина тела l неизменны при деформации, часто закон Гука для деформации растяжения записывают в ином виде

F_упр = k l,

где k = – жесткость.

Д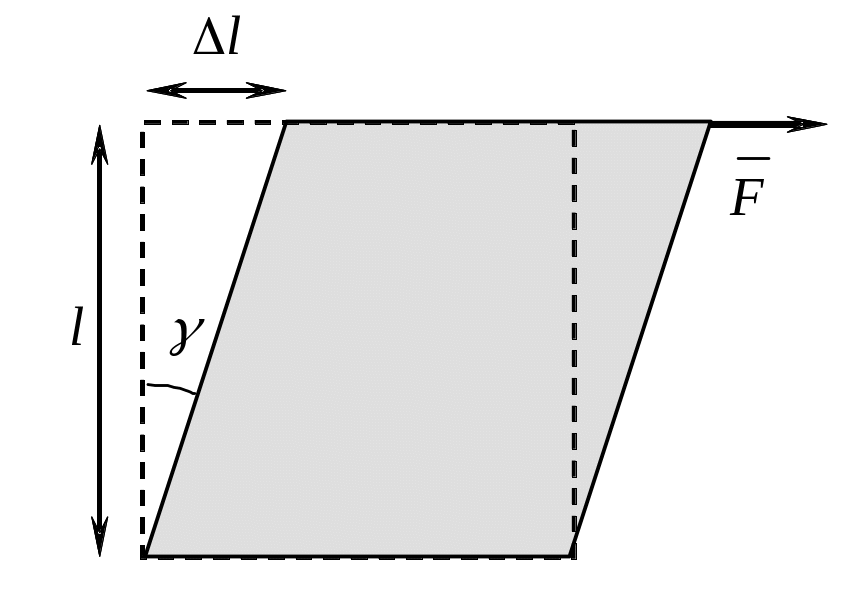 еформация сдвига

Относительный сдвиг при небольших деформациях сдвига

tg  = =  .

Учитывая, что

 = и  = G ,

получим F_упр = G S ,

где G – модуль сдвига.

Деформация кручения

У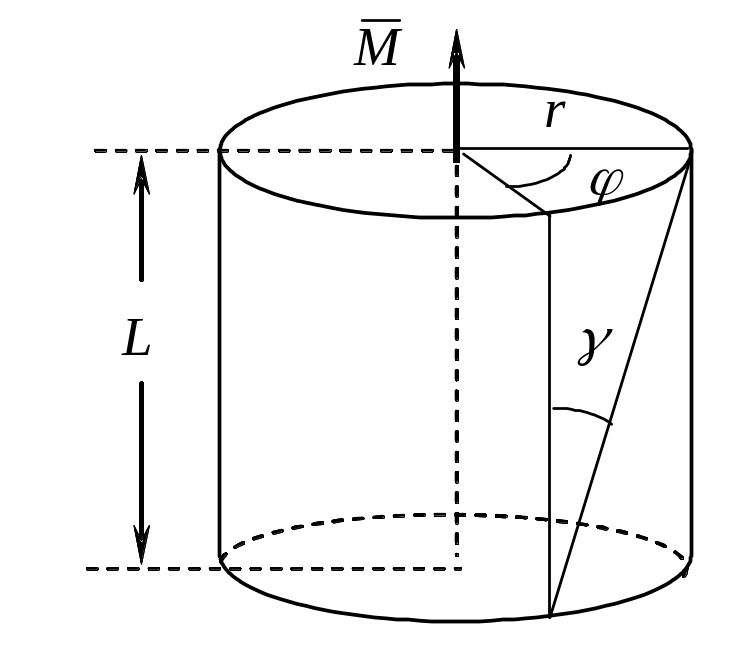 гол поворота φ называется углом кручения. В результате деформации возникает перекос на угол , причем r = L. Расчет деформации кручения может быть сведен к расчету деформации сдвига

M = ,

где G – модуль сдвига для материала стержня.

1.2.2.5. Сила гравитационного взаимодействия

Гравитационное взаимодействие между телами осуществляется с помощью гравитационного поля. На всякое тело массой m, внесенное в поле, действует сила , пропорциональная массе:

= m .

Вектор не зависит от m и называется напряженностью гравитационного поля, он численно равен силе, действующей на тело единичной массы, и совпадает с этой силой по направлению. Вектор является силовой характеристикой гравитационного поля и, в общем случае, является функцией координаты.

Напряженность гравитационного поля

= или G = .

Сила гравитационного взаимодействия

= или F = .

При наложении нескольких гравитационных полей напряженность результирующего поля равна векторной сумме напряженностей этих полей. Этот вывод вытекает из принципа независимости действия сил и называется принципом суперпозиции.

1.3. Законы сохранения в механике

1.3.1. Закон сохранения импульса

Рассмотрим взаимодействие двух тел m₁ и m₂, движущихся до взаимодействия со скоростями ₁ и ₂. Тела взаимодействуют друг с другом силами ₂₁ и ₁₂, которые согласно III закона Ньютона ₂₁ = – ₁₂.

Согласно II закона Ньютона

₂₁dt = и ₁₂dt = .

Тогда + = 0 или + = 0

+ = const.

Аналогично может быть выведен закон сохранения импульса для системы, состоящей из любого числа взаимодействующих между собой тел.

Вектор импульса замкнутой системы тел с течением времени не изменяется, т.е.

= const.

В качестве примера, иллюстрирующего выполнение закона сохранения импульса, рассмотрим отдачу ружья при выстреле. До выстрела система ружье – пуля находится в покое, т.е. их скорости равны нулю. В момент выстрела пуля приобретает скорость (импульс) одного направления, в то время как ружье – в противоположном, при этом скорость ружья во столько раз меньше скорости пули, во сколько раз масса ружья больше массы пули

1.3.2. Закон сохранения момента импульса

Рассматривая вращательное движение а.т.т. можно по аналогии с поступательным движением ввести понятие момента импульса и, проведя рассуждения аналогичные п.4.1., можно сформулировать закон сохранения момента импульса.

Вектор момента импульса замкнутой системы тел с течением времени не изменяется, т.е.

= const.

В качестве примера, иллюстрирующего закон сохранения момента импульса, рассмотрим выполнение акробатом “сальто”. Если после разбега в момент толчка спортсмен сгруппируется, то угловая скорость его вращения будет больше, чем в случае вращения в “полный рост”.

Аналогичного эффекта добиваются фигуристы при исполнении “волчка”. Прижав руки к груди (момент инерции фигуриста при этом уменьшается), спортсмены увеличивают угловую скорость вращения, расставив руки в стороны (момент инерции фигуриста при этом увеличивается) – уменьшают угловую скорость вращения.

1.3.3. Работа. Кинетическая энергия

Работа является мерой воздействия силы.

1.3.3.1. Работа сил и кинетическая энергия поступательного движения

Р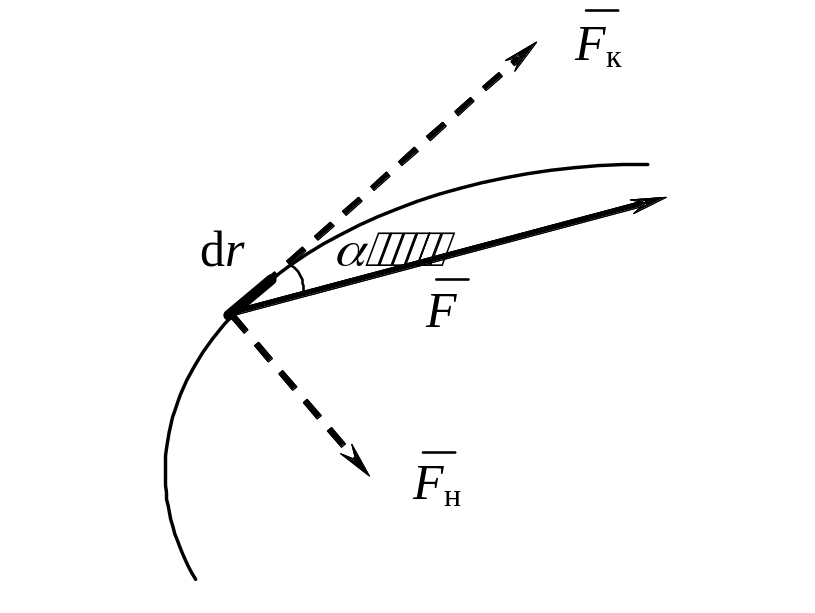 ассмотрим движение тела по некоторой траектории. За промежуток времени dt тело переместится в пространстве на под действием силы .

Перемещающее действие силы можно охарактеризовать работой. Работа силы на бесконечно малом перемещении равно скалярному произведению вектора силы на вектор перемещения

dA = ( ) или dA = F dr cos .

Разложим вектор силы на две взаимно перпендикулярные составляющие: _к – касательная к траектории, т.е. совпадающая по направлению с , _н – нормальная к .

Очевидно, что F_к = F cos .

Тогда

dA = F_к dr.

Работу совершает лишь касательная составляющая силы _к, а работа нормальной составляющей силы _н равна нулю.

Работа на всем пути

A = dA₁ + dA₂ + … + dA_n ,

т.е. A = .

Из 2 закона Ньютона касательная составляющая силы

F_к = m ,

тогда A = = = = 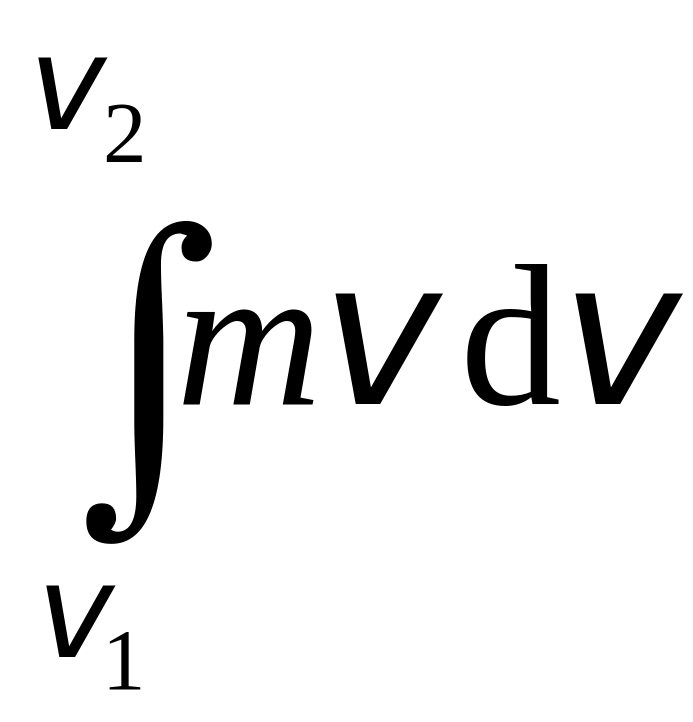mv₂² – mv₁².

Величина mv² = Е_к – кинетическая энергия, тогда

A = Е_к1 – Е_к2 = ΔЕ_к,

т.е. работа A силы на некотором пути численно равна разности кинетических энергий тела в конечном и начальном его положении.

Кинетическая энергия тела зависит только от его массы и величины скорости, от положения тела в пространстве кинетическая энергия не зависит

1.3.3.2. Работа моментa силы и кинетическая энергия вращательного движения

Рассматривая вращательное движение а.т.т. можно по аналогии с поступательным движением ввести понятия работа момента силы и кинетическая энергия вращательного движения тела.

Элементарная работа при вращательном движении тела

dA = М d.

Полная работа

A =

Воспользовавшись основным законом динамики вращательного движения, запишем

A = = d = =  = – .

Кинетическая энергия вращательного движения

Е_к = .

1.3.4. Силы консервативные и неконсервативные

Р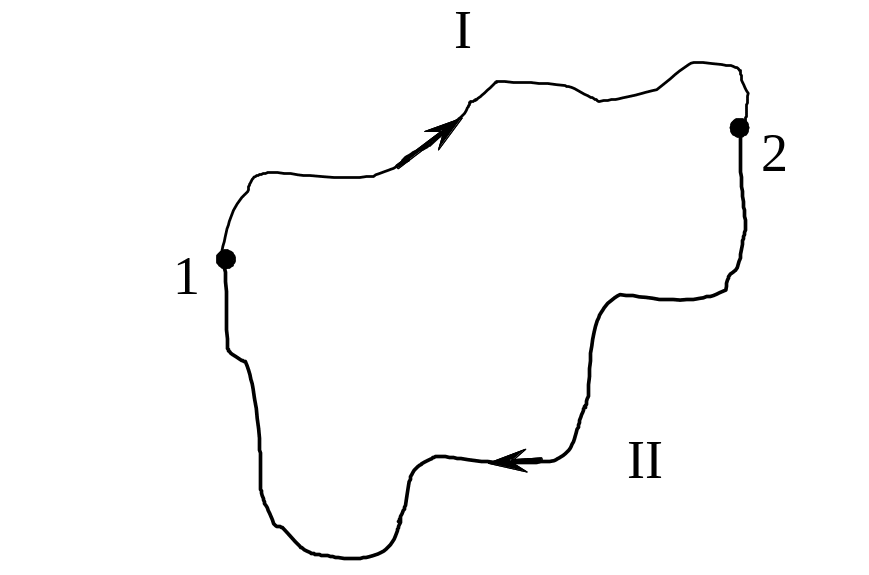 ассмотрим движение частицы в однородном поле сил.

Пусть частица под действием некоторой силы движется по траектории 1–2 затем 2–1. В этом случае работа не зависит от формы пути, а определяется только начальным и конечным положением частицы.

Очевидно, что А₁₂ и А₂₁ равны по величине и отличаются только знаками, следовательно, на всем пути 1–2–1 работа

А = А₁₂ – А₂₁ = 0.

Рассмотрим движение частицы в центральном поле сил.

Р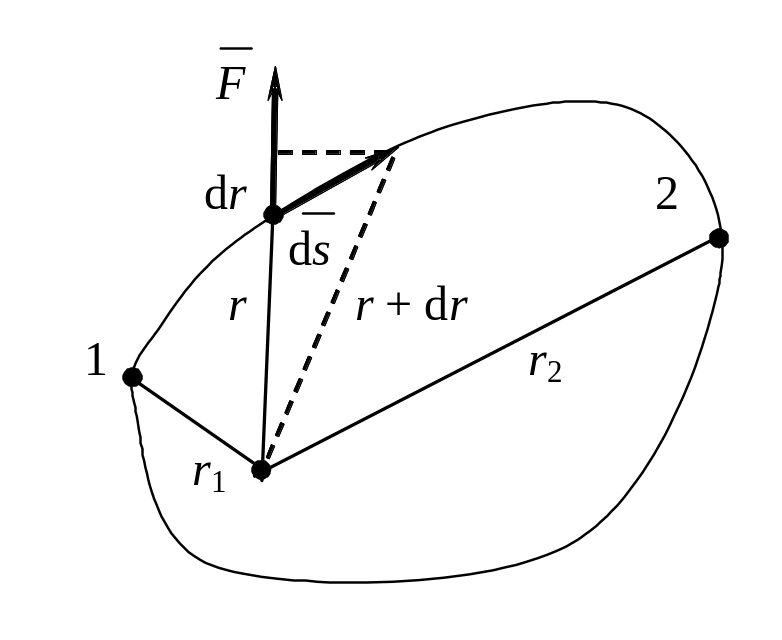 абота силы по перемещению частицы на ds

dA = F ds cos ( ),

ds cos ( ) = dr,

dA = F(r) dr,

A =

Если работа совершается по замкнутой траектории 1–2–1, то А = 0

Силы, работа которых не зависит от пути, по которому тело переходит из одного положения в другое (т.е. работа которых по замкнутому пути равна нулю) называются консервативными силами.

Силы, работа которых не отвечает этим условиям, являются неконсервативными силами.

К неконсервативным силам относятся:

– диссипативные силы – силы, полная работа которых при любых движениях в замкнутой системе всегда отрицательна (например, силы трения);

– гироскопические силы – силы, действующие перпендикулярно скорости движения частицы и зависящие от величины скорости, при этом полная работа при любых движениях равна 0 (например, сила Лоренца и др.)

1.3.5. Потенциальная энергия

Помимо кинетической энергии существует еще один вид механической энергии, связанной с взаимным расположением взаимодействующих частей системы – это потенциальная энергия. Потенциальная энергия Е_р системы является только функцией ее координат.

Зная действующие на тела силы как функции координат, можно вычислить потенциальную энергию системы. В потенциальном поле работа консервативных сил выполняется за счет убыли потенциальной энергии

– d Е_р = ,

это равенство справедливо при любом перемещении

Можно поставить и обратную задачу: вычислить действующую силу по заданной потенциальной энергии Е_р( ) как функции координат взаимодействующих тел.

= – ( )

или

= – .

1.3.5.1. Потенциальная энергия гравитационного взаимодействия тел

По закону всемирного тяготения сила гравитационного взаимодействия

F = .

Работа силы

A = = = 0 – ,

С другой стороны работа определяется разностью энергий до и после взаимодействия

A = Е_р∞ – Е_рr ,

Следовательно

Е_р∞ = 0, Е_рr = – .

В качестве энергетической характеристики гравитационного поля вводится величина _г (потенциал гравитационного поля) равная отношению потенциальной энергии тела в гравитационном поле к массе m этого тела

_г = = – .

1.3.5.2. Потенциальная энергия в однородном поле тяжести

Сила тяжести

F = m g.

Работа силы тяжести

A = = = mgh – 0.

Потенциальная энергия тела в поле силы тяжести

Е_р = mgh.

1.3.5.3. Потенциальная энергия упруго деформированного тела

По закону Гука сила, возникающая при упругой деформации тела

F = .

Работа упругих сил

A = = = – 0 = ,

Потенциальная энергия упругодеформированного тела

Е_р = .

1.3.6. Закон сохранения энергии

Полная энергия изолированной системы материальной точки, равная сумме кинетических энергий точек и потенциальной энергии их взаимодействий, есть величина постоянна:

E = E_к.пост + E_к.вращ + E_р = .

1.3.7. Соударение двух тел

При соударении двух тел они деформируются, при этом кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации и внутреннюю энергию.

Существуют два предельных вида удара: абсолютно упругий удар и абсолютно неупругий удар.

Абсолютно упругий удар. Абсолютно упругий удар – это удар, при котором механическая энергия не переходит в другие, немеханические виды энергии. При таком ударе кинетическая энергия сначала частично или полностью переходит в потенциальную энергию упругой деформации, затем потенциальная энергия переходит в кинетическую энергию. Абсолютно упругий удар описывается законами сохранения энергии и импульса.

Рассмотрим случай абсолютно упругого центрального удара. Центральным называется удар, при котором тела до взаимодействия движутся вдоль прямой, проходящей через их центры.

Пусть массы взаимодействующих тел m₁ и m₂, их скорости до взаимодействия , после взаимодействия тогда

,

.

Решив систему уравнений, получим:

,

.

Абсолютно неупругий удар. Абсолютно неупругий удар характеризуется тем, что потенциальная энергия деформации не возникает; кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара тела слипаются и движутся с одинаковой скоростью. Абсолютно неупругий удар описывается законом сохранения импульса.

Пусть массы взаимодействующих тел m₁ и m₂, их скорости до взаимодействия , после взаимодействия тогда

.

Решив уравнение, получим

.

1.3.8. Гироскопы

Гироскопом называется быстро вращающееся тело, ось вращения которого может изменять свое положение в пространстве.

Теория гироскопа основана на основном уравнении вращательного движения твердого тела и законе сохранения момента импульса.

dt = = .

При кратковременных воздействиях даже очень больших сил движение гироскопа практически не изменится.

Гироскопы обладают свойством сохранять направление оси вращения, а также характер сил, действующих со стороны оси тела на опоры при внешних воздействиях.

Если к вращающемуся гироскопу приложить пару сил, стремящихся повернуть его около оси, перпендикулярной к оси его вращения, то он станет поворачиваться около третьей оси, перпендикулярной к первым двум.

Если к гироскопу, вращающемуся относительно оси yy’ приложить пару сил ’, перпендикулярную оси вращения и направленную вдоль оси z z’, то ось вращения повернется вдоль оси zz’, верхний конец оси гироскопа в направлении , нижний – в направлении ’. В результате гироскопического эффекта гироскоп стремится расположить ось своего вращения таким образом, чтобы она образовывала возможно меньший угол с осью вынужденного вращения xx’ и чтобы оба вращения совершались в одном и том же направлении.

П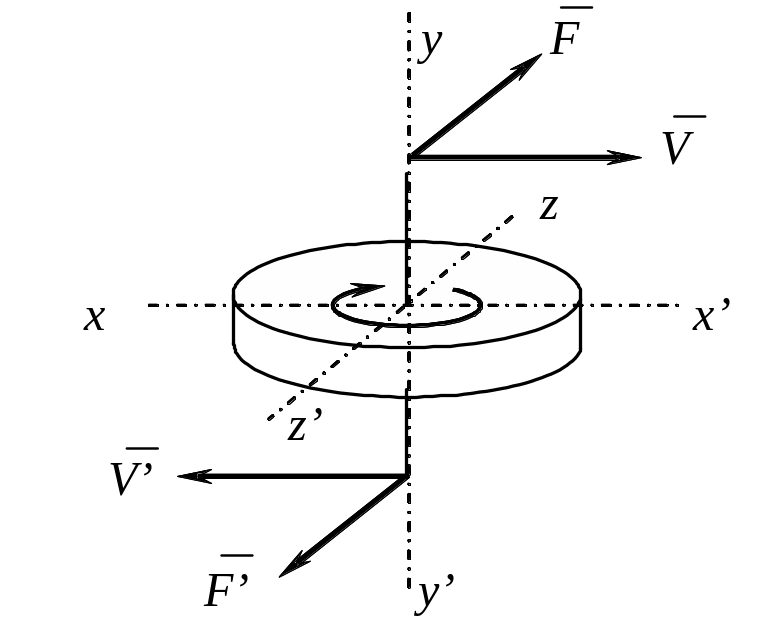 ри действии на ось вращения гироскопа пары сил ’ возникает момент сил, направленный вдоль оси xx’, что приводит к изменению направления вектора момента импульса и повороту оси вращения на угол .

Гироскопические силы проявляются и при движении обыкновенного волчка. При наклонном положении вращающегося волчка сила тяжести стремится наклонить его еще больше, но благодаря гироскопическому эффекту ось начинает двигаться. В результате прецессии волчок не падает.

1.4. ДВИЖЕНИЕ ЖИДКОСТИ и газа

(ЭЛЕМЕНТЫ ГИДРО- И АЭРОДИНАМИКИ)

Рассмотрим применение основных законов динамики к простейшим случаям движения жидкости. Под понятием жидкость будем объединять и собственно жидкости (воду, спирт, ртуть и другие тела в жидком агрегатном состоянии), и газы. Общим для обоих случаев является то, что в отличие от твердого тела отдельные частицы жидкости могут перемещаться друг относительно друга, и жидкость, помещенная в какой-либо сосуд, заполняет его и принимает форму сосуда.

Ограничимся простейшим случаем движения жидкости, когда выполняются следующие три условия.

Жидкость несжимаема, т.е. плотность  отдельных движущихся элементов объема жидкости остается во все время движения постоянной.

Для жидкостей подобное приближение вполне естественно, так как их сжимаемость очень невелика. В противоположность жидкостям газы сжимаются легко, и их плотность прямо пропорциональна давлению. Благодаря малому значению плотности для приведения газа в движение достаточно очень малого изменения давления, а следовательно, и плотности газа.

Теория и опыт показывают, что сжимаемостью жидкости или газа можно пренебрегать и с достаточной степенью точности пользоваться понятием несжимаемой жидкости при условии, что скорости их движения малы по сравнению со скоростью распространения звука (v_зв = 333 м/сек).

Понятие несжимаемости характеризует не столько свойства самой жидкости при отсутствии движения, сколько свойства данного движения. И жидкости, и газы при движении практически несжимаемы, когда

v_движ << v_зв

Жидкость идеальна, т.е. отдельные элементы жидкости движутся друг относительно друга без трения. Справедливость подобного пренебрежения трением также зависит от характера изучаемого движения. При движении реальной жидкости или газа внутри нее всегда возникают силы вязкости. Мы будем называть жидкость идеальной тогда, когда во время ее движения можно пренебречь силами внутреннего трения по сравнению с другими силами, действующими в жидкости (силами тяжести, давления и т. п.). В этих случаях потери энергии движения на трение и переход в тепло незначительны и можно применять закон сохранения энергии в чисто механической форме.

Движение жидкости установившееся. Если внешние силы, вызывающие движение жидкости, не зависят от времени, то через некоторое время после начала движения в жидкости установится вполне определенное распределение скоростей. При этом скорость движения каждой частицы жидкости может изменяться от точки к точке вдоль ее траектории. Однако в каждой данной точке пространства скорости движения всех последовательно проходящих через нее частиц жидкости будут одинаковыми. Такое движение жидкости в данной ограниченной части пространства и называется установившимся.

Д.Бернулли вывел соотношение для установившегося движения идеальной несжимаемой жидкости, носящее название уравнения Бернулли.

Д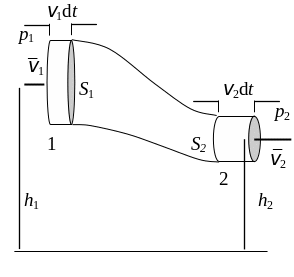 ля вывода этого уравнения рассмотрим жидкость, движущуюся по трубе переменного сечения. Жидкость втекает слева в сечение 1 площадью S₁, находящееся на высоте z₁ над уровнем земли. Скорость втекающих частиц жидкости перпендикулярна к сечению трубы и равна v₁, давление в жидкости при входе в трубу равно p₁.

Через сечение 2 площадью S₂, находящееся на высоте h₂ над уровнем земли, жидкость вытекает из трубы со скоростью v₂ давление в жидкости на выходе из трубы равно р₂. Жидкость течет через трубу под действием разности приложенных извне давлений p₁ – р₂ или разности уровней h₁ – h₂, приводящей к гидростатическому давлению соответствующего столба жидкости, или того и другого вместе.

За бесконечно малый промежуток времени dt через сечение S₁ втекает масса жидкости dm, заполняющая цилиндрик с площадью основания S₁ и высотой v₁dt (заштрихованный на рисунке). За тот же промежуток времени через сечение 2 вытечет такая же масса жидкости dm, заполнявшая цилиндрик с площадью основания S₂ и высотой v₂dt (также заштрихованный на рисунке). Значение dm можно найти, умножив величину каждого из этих элементарных объемов на плотность жидкости ρ. Тогда получим:

dm = ρ S₁ v₁ dt = ρ S₂ v₂ dt.

Для несжимаемой жидкости на основании закона сохранения вещества всегда выполняется соотношение, называемое уравнением неразрывности:

ρ S₁ v₁ = ρ S₂ v₂ или

При перемещении массы жидкости dm по трубе силы внешнего давления совершают работу. Полная сила давления, действующая на левое сечение, равна p₁S₁. Эта сила переместила массу жидкости dm на расстояние v₁dt. За то же время в правом сечении такая же масса жидкости dm переместилась на расстояние v₂dt и совершила работу против силы давления p₂S₂.

Полная работа А сил давления при таком перемещении равна

А = p₁ S₁ v₁ dt – p₂ S₂ v₂ dt

Эта работа затрачена на увеличение кинетической энергии элемента жидкости с массой dm, скорость которого изменилась от v₁ на входе до v₂ на выходе, и на изменение потенциальной энергии этого элемента в поле тяжести при переходе с уровня h₁ на уровень h₂. Следовательно,

p₁ S₁ v₁ dt – p₂ S₂ v₂ dt = ,

p₁ – p₂ = .

p₁ + = p₂ + .

Поскольку сечения 1 и 2 могут быть выбраны произвольно, то в любом сечении трубы

p + =const.

Данное уравнение называется уравнением Бернулли и выражает закон сохранения энергии при установившемся движении несжимаемой идеальной жидкости. Это уравнение справедливо для любого движущегося объема жидкости вдоль траектории его движения, называемой линией тока.

Величина представляет собой удельную кинетическую энергию, т.е. кинетическую энергию единицы объема движущейся жидкости. Величина есть удельная потенциальная энергия в поле тяжести. Соответственно этому, величина р представляет собой удельную потенциальную энергию сил давления в жидкости.

При движении элементарного объема жидкости происходит непрерывный переход его энергии из одной формы в другую, но полная энергия этого объема остается неизменной.

Так как все члены уравнения Бернулли имеют размерность давления, то это уравнение часто формулируют иначе. Давление р называют статическим напором, величину – гидравлическим напором, а величину – скоростным, или динамическим, напором.

Тогда следует, что полный напор в движущейся жидкости, складывающийся из статического, гидравлического и скоростного напоров, остается постоянным.

Приведем для пояснения два примера.

Н а рисунке изображена схема водоструйного насоса. Поток воды из водопровода течет по трубке с местным сужением. В узком сечении скорость жидкости резко возрастает и увеличивается скоростной напор . При этом по уравнению Бернулли в суженном сечении падает статический напор и давление р₂ становится ниже атмосферного. Поэтому через отводную трубку в это сечение засасывается воздух из откачиваемого сосуда А. Пройдя суженное сечение, струя воды с воздухом вновь расширяется, ее скорость падает, а давление возрастает до атмосферного на выходе из насоса.

Такой насос очень прост по конструкции и может создавать значительное разрежение, понижая давление в откачиваемом сосуде до ~ 10 ^–3 атм.

Работами Д. Бернулли и его современника Эйлера были заложены основы науки о движении жидкостей, выросшей в настоящее время в самостоятельную науку – гидродинамику. Широкое практическое применение гидродинамика получила в конце XIX и начале XX веков в результате работ Н.Е.Жуковского и С.А.Чаплыгина. Ими была создана также новая наука – аэродинамика – учение о законах движения газов и теория полета. Жуковскому первому удалось объяснить механизм подъемной силы, создаваемой крылом аэроплана при движении. На рисунке изображен разрез примерного профиля крыла. Пунктиром показаны линии тока встречного течения воздуха. Как видно из рисунка, над верхней частью крыла происходит сгущение этих линий и увеличение относительной скорости воздушного потока. Согласно уравнению Бернулли давление в потоке над крылом станет меньше, чем под крылом, и за счет этой разности давлений возникает подъемная сила F, удерживающая летящий самолет в воздухе.

Н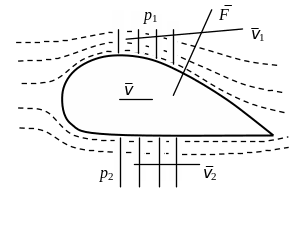 а основе этой качественной картины Н.Е.Жуковский разработал количественные методы расчета величины подъемной силы для различных профилей крыла. Созданные им профили, ныне называемые профилями Жуковского, позволили проектировать крылья наивыгоднейшей формы.

При скоростях полета современных скоростных самолетов воздух уже нельзя считать несжимаемой жидкостью. Методы учета сжимаемости воздуха были разработаны С.А.Чаплыгиным еще в 1903 г., когда скорости полета не превышали 30–40 км/час. На основе этих методов рассчитываются подъемная сила и сопротивление крыльев при современных скоростях полета.

1.5. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Колебательное движение – это движение, при котором тело, выйдя из положения равновесия, периодически возвращается к нему.

Если этот возврат совершается через равные промежутки времени, то колебания называются периодическими колебаниями.

Простейшим случаем периодических колебаний являются гармонические колебания.

1 .5.1. Гармонические колебания

Пусть точка D равномерно с угловой скоростью w вращается по окружности радиусом А, тогда угловая координата точки будет меняться согласно уравнению

 = ₀ + t,

где ₀ – значение угла при t = 0.

Проекция точки D на ось 0х меняется согласно уравнению

х = А cosj = А cos(j₀ + wt),

проекция точки на ось 0у

у = А sinj = А sin(j₀ + wt),

j₀ не влияет на характер движения, а означает лишь изменение начального момента в отсчете времени.

Сos j и sinj являются периодическими функциями от t с периодом

.

Период колебания – промежуток времени, в конце которого точка оказывается в том же положении и движется с той же скоростью, как и в его начале.

Таким образом, точки M и N совершают периодические колебания.

Периодические колебания, при которых смещение меняется по закону sin или cos называются гармоническими колебаниями.

Очевидно, что проекция точки D на любую прямую, и не проходящую через 0, будет совершать гармонические колебания.

В уравнении гармонического колебания х = А cosj = А cos(j₀ + wt)

А – максимальная величина смещения – амплитуда колебания; j – фаза колебания; j₀ – начальная фаза колебания; w – угловая скорость вращения точки D – циклическая частота.

Циклическая частота введена в связи с тем, что гармонические колебания – не обязательно проекция движения точки по окружности, например, рассматривая колебания груза на пружине или поплавка в жидкости не удобно описывать такие колебания, пользуясь понятием “угловая скорость”,

Зная уравнение смещения точки при гармоническом колебании

х = А cosj = А cos(j₀ + wt),

легко найти уравнения изменения других кинематических и динамических характеристик.

Скорость движения точки

v = = – wА sinj = – wА sin(j₀ + wt).

Ускорение движения точки

a = = – w²А cosj =

= – w²А cos(j₀ + wt)

или a = – w² х .

Из полученных уравнений и их графического представления следует:

– смещение х, скорость v, ускорение а точки меняются гармонически с одинаковой циклической частотой w и периодом Т;

– амплитуда колебаний |х_max | = |A|, |v_max| = |ωА|, |a _max| = |Aω²|;

– фазы колебаний различны:

– колебания скорости опережают колебания смещения на 0,5,

– колебания ускорения опережают колебания смещения на .

Например, при прохождении положения равновесия х = 0 и возрастает, v = v_max , а = 0 и убывает.

Сила, действующая на точку

F = ma = – m w²А cos(j₀ + wt) = – m w² х

или F = – m w² х ,

т.е. направление силы противоположно направлению смещения, т.е. сила всегда направлена к положению равновесия.

Из выше изложенного следует

ma = – m w² х ,

= – w² х ,

+ w² х = 0

последнее уравнение является дифференциальным уравнением гармонических колебаний.

Кинетическая энергия колеблющейся точки

Е_к = mv² = m w²А² sin² (j₀ + wt).

Потенциальная энергия точки, колеблющейся под действием упругих сил

Е_р = = m w²А² cos²(j₀ + wt).

П олная энергия колеблющейся точки

Е = Е_к + Е_р = m w²А² sin²(j₀ + wt) + m w²А² cos²(j₀ + wt) = m w²А².

Е = Е_{к max} = Е_{р max}

1.5.2. Колебания под действием упругих и квазиупругих сил

1.5.2.1. Колебания груза на пружине

С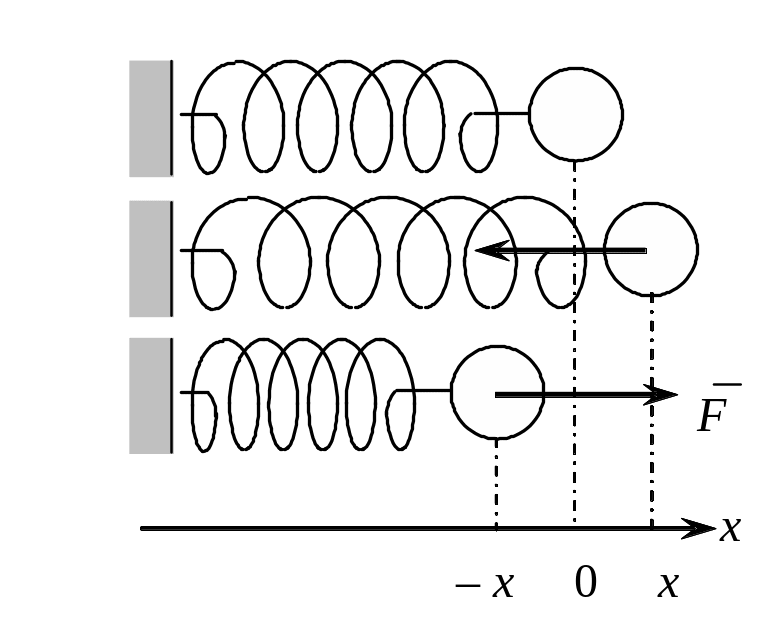 ила, действующая на груз, закрепленный на пружине

F = – kx.

Сила, действующая на тело, совершающее гармонические колебания

F = – m w² х .

Очевидно, что и в первом, и во втором случае зависимость силы от смещения подчиняется одинаковым закономерностям, и, следовательно, груз на пружине совершает гармонические колебания. При этом

k = m ω² , w = , Т = .

1.5.2.2. Колебания поплавка

На поплавок в положении равновесия действуют: сила тяжести mg и сила Архимеда F_A = gV.

П риращение силы, действующей на поплавок, выведенный из положения равновесия F = – gS x, знак “минус” означает, что направление силы и смещения не совпадают.

Сила, действующая на тело, совершающее гармонические колебания

F = – m w² х .

Очевидно, что поплавок в жидкости совершает гармонические колебания. При этом

k = gS , w = , Т = .

1.5.2.3. Колебания математического маятника

Н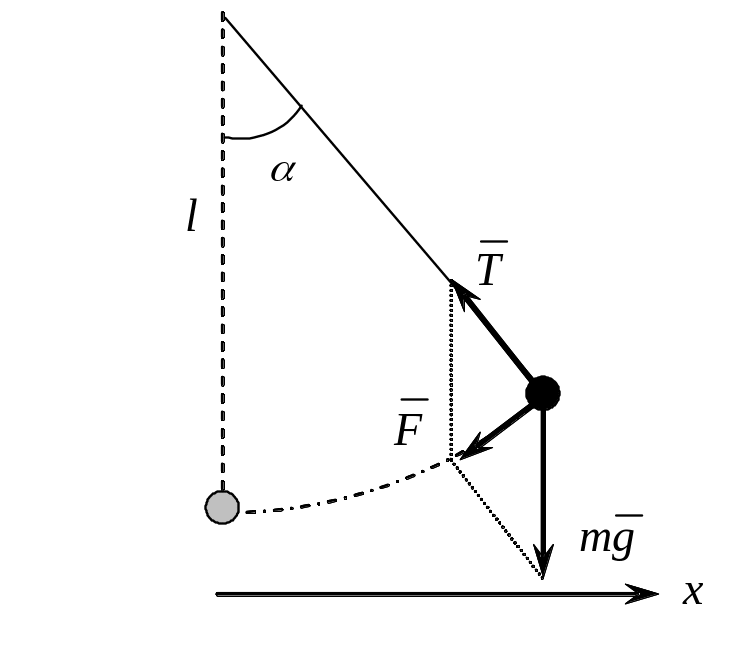 а математический маятник действуют: сила тяжести и сила натяжения нити . Результирующая сила

F = – mg sin = – mg ,

знак “минус” означает, что направление силы и смещения не совпадают.

Сила, действующая на тело, совершающее гармонические колебания

F = – m w² х .

Очевидно, что математический маятник совершает гармонические колебания. При этом

k = , w = , Т = .

1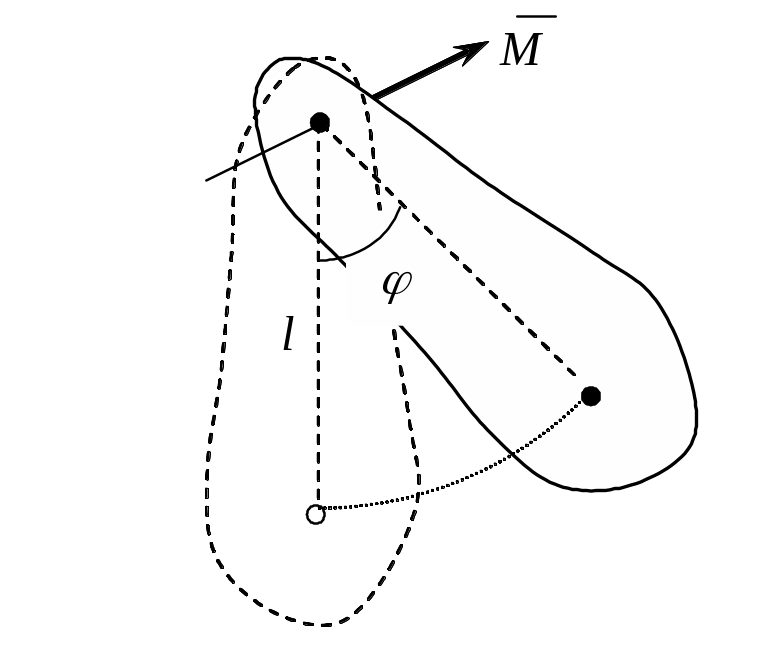 .5.2.4. Колебания физического маятника

При отклонении маятника от положения равновесия возникает возвращающий момент

М = – mgl sinj,

знак “минус” означает, что направление момента силы и углового смещения не совпадают.

Из основного уравнения вращательного движения

М = I ε = I .

Тогда – mgl sinj = I ,

I + mgl j = 0.

+ = 0,

что соответствует уравнению гармонических колебаний, т.е. физический маятник совершает гармонические колебания. При этом

w = , Т = .

1.5.3. Сложение гармонических колебаний

1.5.3.1. Сложение гармонических колебаний одного направления

Рассмотрим несколько частных случаев

а) А₁  А₂, w₁ = w₂, j₀₁  j₀₂.

Точка одновременно участвует в двух колебаниях

х₁ = А₁ cosj₁ = А₁ cos(j₀₁ + w₁t),

х₂ = А₂ cosj₂ = А₂ cos(j₀₂ + w₂t).

Тогда результирующее смещение точки равно алгебраической сумме обоих смещений

х = х₁ + х₂ = А₁ cosj₁ + А₂ cosj₂ = А₁ cos(j₀₁ + w₁t) + А₂ cos(j₀₂ + w₂t).

Для анализа движения построим векторную диаграмму.

Так как w₁ = w₂, то угол между векторами А₁ и А₂ не меняется

 = j₁ – j₂ = j₀₁ + ω₁t – j₀₂ – ω₂t =

= j₀₁ + j₀₂.

Амплитуду колебания А может быть найдена по теореме косинусов

А² = А₁² + А₂² + 2 А₁А₂ cos(j₁ – j₂) = А₁² + А₂² + 2А₁А₂ cos(j₀₁ – j₀₂) =

= А₁² + А₂² + 2 А₁А₂cos

Начальная фаза результирующего колебания может быть найдена из соотношения

tgj₀ = ,

циклическая частота w = w₁ = w₂.

б) А₁  А₂, ω₁ = ω₂, j₀₁ = j₀₂.

Точка одновременно участвует в двух колебаниях

х₁ = А₁ cosj₁ = А₁ cos(j₀₁ + w₁t),

х₂ = А₂ cosj₂ = А₂ cos(j₀₂ + w₂t).

Тогда результирующее смещение точки равно алгебраической сумме обоих смещений

х = х₁ + х₂ = А₁ cosj₁ + А₂ cosj₂ = (А₁ + А₂) cos(j₀ + wt).

Очевидно, что амплитуду результирующего колебания А = А₁ + А₂, циклическая частота w = w₁ = w₂, а начальная фаза j₀ = j₀₁ = j₀₂

в) А₁ = А₂ , w₁ = w₂ , j₀₁  j₀₂.

Точка одновременно участвует в двух колебаниях

х₁ = А₁ cosj₁ = А₁ cos(j₀₁ + w₁t),

х₂ = А₂ cosj₂ = А₂ cos(j₀₂ + w₂t).

Тогда результирующее смещение точки равно алгебраической сумме обоих смещений

х = х₁ + х₂ = А₁ cosj₁ + А₂ cosj₂ = А₁ cos(j₀₁ + w₁t) + А₂ cos(j₀₂ + w₂t) =

= А₁ [cos(j₀₁ + w₁t) + cos(j₀₂ + w₂t)] =

= 2 А₁ [cos + cos ] =

= 2 А₁ [cos cos( )].

Очевидно, что результирующее колебание имеет:

амплитуду А = 2 А₁ cos ,

начальную фазу j₀ = ,

циклическую частоту w = w₁ = w₂,

в) А₁ = А₂ , w₁  w₂ (w₁ – w₂ << w₁, w₂), j₀₁ = 0, j₀₂ = 0

Точка одновременно участвует в двух колебаниях

х₁ = А₁ cosj₁ = А₁ cosw₁t,

х₂ = А₂ cosj₂ = А₂ cosw₂t.

Тогда результирующее смещение точки равно алгебраической сумме обоих смещений

х = х₁ + х₂ = А₁ cosj₁ + А₂ cosj₂ = А₁ cosw₁t + А₂ cosw₂t =

= А₁ (cosw₁t + cosw₂t) = 2 А₁ cos t cos t.

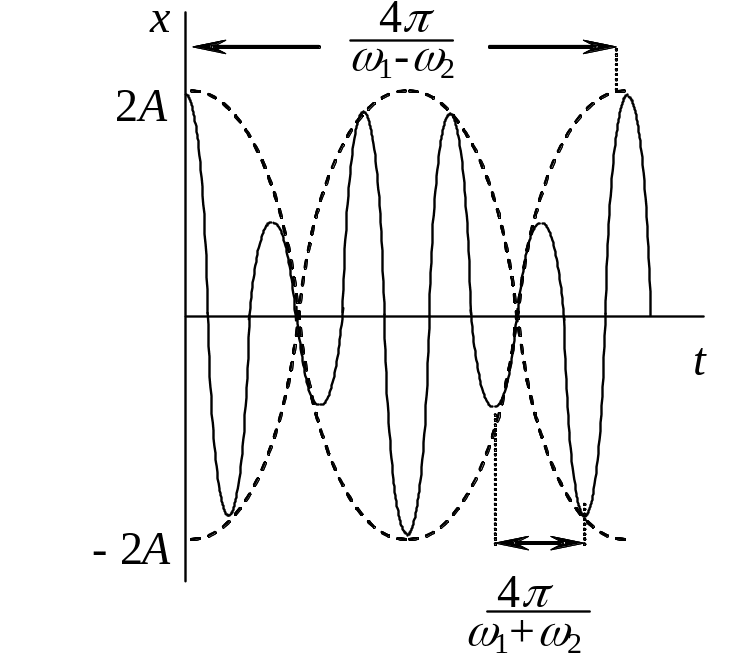О чевидно, что амплитуду результирующего колебания

А = 2 А₁ cos t

зависит от времени и изменяется с “биениями”, начальная фаза j₀ = 0, а циклическая частота

w = .

1.5.3.2. Сложение взаимноперпендикулярных гармонических

колебаний

Точка одновременно участвует в двух колебаниях

х = А₁ cos(j₀₁ + w₁t),

y = А₂ cos(j₀₂ + w₂t).

Рассмотрим несколько частных случаев

а) w₁ = w₂ = w.

= cosj₀₁ coswt – sinj₀₁ sinwt ,

= cosj₀₂ coswt – sinj₀₂ sinwt ,

Умножим первое уравнение на cosj₀₂, второе – на cosj₀₁ и вычтем второе уравнение из первого:

cosj₀₂ – cosj₀₁ = sinwt sin(j₀₂ – j₀₁).

Умножим исходные уравнения на sinj₀₂ и на sinj₀₁ соответственно и вычтем второе уравнение из первого:

sinj₀₂ – sinj₀₁ = coswt sin(j₀₂ – j₀₁).

В озведем полученные уравнение в квадрат и сложим их:

+ – cos (j₀₂ – j₀₁) =

= sin² (j₀₂ – j₀₁).

Полученное уравнение является уравнением эллипса, оси которого повернуты относительно координатных осей x и y.

б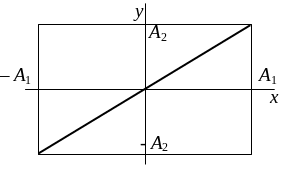 ) w₁ = w₂, j₀₁ = j₀₂.

Тогда

или y = x.

Траектория представляет прямую линию – диагональ прямоугольника со сторонами 2А₁ (по оси х) и 2А₂ (по оси у)

в) w₁ = w₂, j₀₂ = j₀₁ + .

Тогда

или y = x.

Траектория представляет другую диагональ прямоугольника

г ) w₁ = w₂, j₀₂ = j₀₁ + .

Тогда = cos(j₀₁ + w₁t),

= cos(j₀₂ + w₂t).= sin(j₀₁ + w₁t),

+ = cos²(j₀₁ + w₁t) + sin²(j₀₁ + w₁t) = 1.

Траектория представляет собой эллипс c направлением обхода по часовой стрелке. При А₁ = А₂ = А траектория превращается в окружность радиуса А.

д) w₁ = w₂, j₀₂ = j₀₁ – .

Траектория останется той же (г), но изменится направление обхода.

Таким образом, в случае равных частот суммарное колебание происходит в общем случае по эллипсу (прямые (б) и (в) следует рассматривать как вырожденный эллипс). Амплитуды складываемых колебаний определяют значение осей эллипса, а сдвиг фаз определяет вид эллипса и направление его обхода.

Более сложные кривые получаются при неравных частотах. В случае рационального отношения частот будут иметь место различные кривые, вид которых зависит от отношения частот и сдвига начальных фаз:

е ) w₂ = 2 w₁, j₀₂ = j₀₁. ж) w₂ = 2 w₁, j₀₂ = j₀₁+ .

з ) 3 w₂ = 2 w₁, j₀₂ = j₀₁. и) 4 w₂ = 3 w₁, j₀₂ = j₀₁.

1.5.4. Затухающие колебания

В условиях, когда на тело действует только одна квазиупругая сила, оно будет совершать незатухающие гармонические колебания с постоянной амплитудой A = const. На реально же движущиеся nела всегда будут воздействовать со стороны окружающей среды силы трения, препятствующие их движению. На преодоление сопротивления среды и т.п. будет затрачиваться энергия. Вследствие этого механическая энергия колеблющегося тела будет непрерывно уменьшаться, переходя в другие формы энергии и рассеиваясь в окружающую среду. С уменьшением энергии колебания будет уменьшаться его амплитуда, и колебание станет затухающим. Полная сила F, действующая на колеблющуюся точку, будет тогда суммой квазиупругой силы F_{кв–упр} и силы трения F_тр. При малых скоростях движения сопротивление обычно пропорционально первой степени скорости и направлено противоположно ей, т.е.

F_тр = – rv = – r ,

где r — коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.

На основании 2 закона Ньютона получим дифференциальное уравнение одномерного движения материальной точки массы m под действием квазиупругой силы и силы трения

m = – r – kx .

m + r + kx.= 0.

Решение данного дифференциального уравнения имеет вид:

x = A₀ e^–t cos(wt+j₀)

где  = – коэффициент затухания – физическая величина, обратная промежутку времени  (время релаксации), в течение которого амплитуда убывает в е раз;

w = = – циклическая частота затухающих колебаний,

w₀ – циклическая частота собственных колебаний точки при отсутствии трения.

Чем больше коэффициент трения r, тем больше величина α в показателе степени и тем быстрее амплитуда затухающих колебаний убывает со временем.

При наличии трения не только убывает со временем амплитуда колебания, но и уменьшается угловая частота колебаний.

С увеличением трения период колебаний возрастает, и при r = 2m w₀, т.е. a = w₀ период становится бесконечным (Т = ∞). При дальнейшем увеличении a период Т становится мнимым, а движение точки – апериодическим.

1.5.5. Вынужденные колебания. Резонанс

Для получения незатухающих колебаний необходимо воздействие дополнительной переменной внешней силы, которая подталкивала бы точку то в одну, то в другую сторону и работа которой непрерывно восполняла бы убыль энергии, затрачиваемой на преодоление трения. Подобная переменная сила называется вынуждающей (F_вын), а возникающие под ее действием незатухающие колебания – вынужденными.

Разберем простейший случай вынуждающей силы, меняющейся по закону синуса или косинуса, т.е. положим

F_вын = F₀ cos(t)

где F₀ – есть амплитуда вынуждающей силы,  – угловая частота колебаний вынуждающей силы.

Полная сила, действующая на колеблющуюся точку, будет алгебраической суммой квазиупругой силы, силы трения и вынуждающей силы, и дифференциальное уравнение движения примет вид

m = – r – kx + F₀ cos(t),

решение этого уравнения

x(t) = x_своб(t) + x_вын(t),

п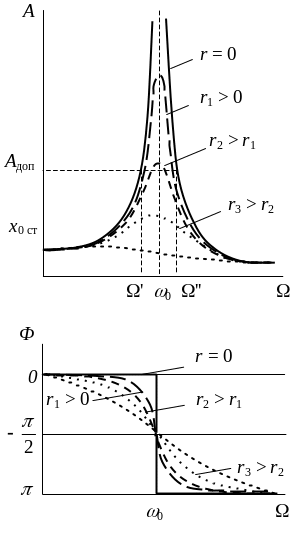 редставляет собой сумму свободных колебаний x_своб(t) и вынужденных колебаний x_вын(t). Свободные колебания будут происходить с собственной угловой частотой w = и быстро затухнут, а частота вынужденных колебаний совпадает с частотой вынуждающей силы. Амплитуда этих колебаний должна быть постоянной, поскольку амплитуда вынуждающей силы не меняется со временем. Поэтому, собственными колебаниями системы, играющими существенную роль лишь в самом начале процесса, можно пренебречь.

Тогда решение уравнения будет иметь вид

x(t) = x_вын(t) = А cos(t + Ф),

где А = – амплитуда вынужденных колебаний,

Ф = arctg – сдвиг фазы

x_вын(t) не зависит от начальных условий движения, когда в силу затухания x_своб(t) обратится в нуль, колебательное движение будет определяться только свойствами колеблющейся системы и амплитудой и частотой вынуждающей силы.

Под действием периодической вынуждающей силы F_вын возникают гармонические вынужденные колебания с частотой . Амплитуда вынужденных колебаний А прямо пропорциональна амплитуде вынуждающей силы F₀, зависит от характеристик свободно колеблющейся точки т, k и r и является функцией угловой частоты колебаний вынуждающей силы . Графики зависимости А и сдвига фаз Ф от  (для нескольких значений r) представлены на рисунке.

Как видно из этих графиков, характер этих зависимостей различен в трех областях изменения угловой частоты .

1) область малых частот:

В этой области сдвиг фаз Ф близок к нулю, а выражение для амплитуды можно преобразовать к виду

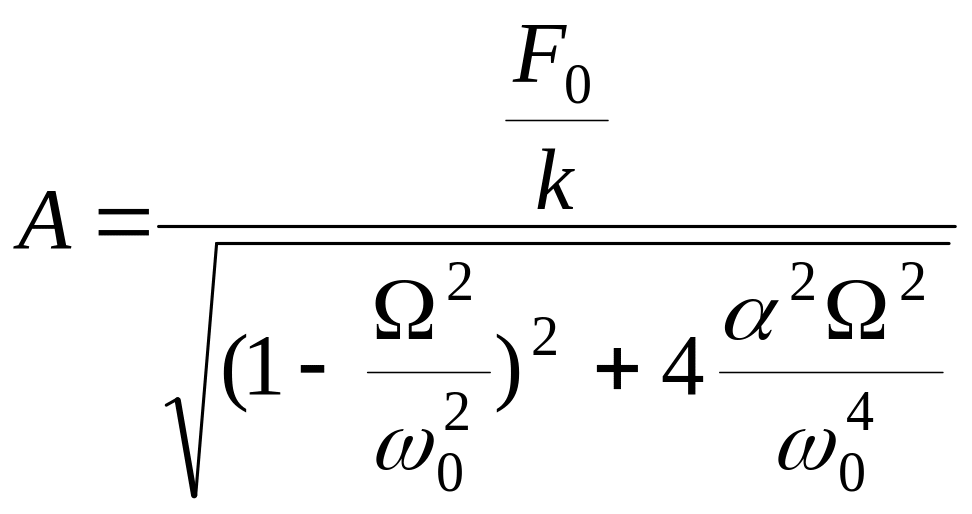
В предельном случае, когда  = 0 (при постоянной нагрузке),

А = = x_0ст ,

где x_{0 ст} – статическое смещение точки под действием постоянной силы F = F₀. При 0 <  << ω₀ и малом трении (a << w₀) получим

x ≈ cost =

т.е. смещение колеблющейся точки почти без искажений следует за изменением вынуждающей силы. Этот случай представляет практический интерес для измерительной техники.³

2) область высоких частот:

При таких частотах Ф ≈ –  и колебания точки происходят в фазе, противоположной колебаниям вынуждающей силы. Когда смещение положительно, вынуждающая сила отрицательна, и наоборот. Вследствие этого амплитуда вынужденных колебаний не может быть большой и убывает с ростом частоты вынуждающей силы по закону

A = x_{0 ст}

Подобный случай также имеет важное практическое значение.⁴.

3) область резонанса:

При частотах колебания вынуждающей силы, близких к частоте собственных колебаний системы, амплитуда вынужденных колебаний сильно возрастает и начинает во много раз превышать статическое смещение:

A ≈ x_{0 ст}

Чем меньше коэффициент трения, тем больше эта амплитуда. В пределе, А → ∞ при r → 0. Это явление резкого возрастания амплитуды вынужденных колебаний при  ≈ w₀ носит название механического резонанса.

Явления резонанса широко распространены в природе и технике⁵.

1 Когда речь идет только о линейных скоростях и другие скорости (угловые) не рассматриваются, термин «линейная» обычно опускается.

2 Существует три понятия, имеющие одинаковое название: масса, как мера инертности; масса, как мера количества вещества; масса, как мера гравитационного взаимодействия. Однако численного различия между ними не установлено.

3 Различные самопишущие приборы для регистрации быстропеременных усилий (например, мембранный индикатор, записывающий давление в быстроходном двигателе) представляют собой системы, на которые действуют упругие или квазиупругие силы, возвращающие систему в положение равновесия после снятия нагрузки. Переменное усилие является для такой системы вынуждающей силой со своей характерной угловой частотой  (или несколькими угловыми частотами _i). Чтобы вынужденные колебания прибора успевали следовать за изменениями вынуждающей силы, собственная частота колебаний прибора ω₀ должна быть во много раз больше частоты изменения измеряемой величины Ω. При ω₀ > 10 ошибка измерений не будет превышать 1–2%. Увеличение собственной частоты ω₀ достигается как за счет увеличения жесткости измерительной системы k, так и за счет уменьшения ее массы т (с ростом k и уменьшением т величина tgФ → 0, а следовательно, и сдвиг фаз Ф → 0)

4 Например, для предотвращения воздействия качки корабля на различные приборы их следует подвешивать на сравнительно мягких пружинах и максимально утяжелять. Если при этом частота собственных колебаний системы w₀ будет сделана много меньше частоты качки , то амплитуда колебаний подвешенного прибора будет много меньше амплитуды колебаний точки подвеса.

5 Когда войсковая часть идет по мосту, то обязательно подается команда идти «не в ногу». Периодические толчки, создаваемые строем солдат при ходьбе «в ногу», могут попасть в резонанс с собственными колебаниями моста и привести к его разрушению. Маломощный двигатель, если он плохо уравновешен и при вращении «бьет», может в случае резонанса разрушить или сильно повредить сооружение, на котором он укреплен, и т.п

С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если частота их совпадает с частотой собственных колебаний прибора. Вся прикладная акустика и радиотехника, аппараты, воспринимающие звуковые и электрические колебания, основаны на явлениях резонанса. Возможность поддерживать незатухающие колебания представляет чрезвычайный интерес для техники. Особенно важными и широко применяемыми являются колебательные движения, возникающие и поддерживающиеся за счет постоянного, неколебательного источника энергии. Такие системы называются автоколебательными. В качестве примеров автоколебательных систем можно привести: часы, в которых постоянные колебания маятника поддерживаются за счет энергии спиральной пружины или поднятого груза; радиопередатчик, энергия колебаний которого поддерживается за счет энергии аккумуляторных батарей; электрический звонок, пневматический молоток и многие другие приборы.

Чтобы колебательное движение не затухало, к колеблющейся системе необходимо подводить энергию для компенсации ее потерь в процессе колебаний. Подвод энергии осуществляется в виде «толчков» в подходящие моменты времени. Толчок должен ускорить, а не замедлить колебание. В автоколебательной системе включение источника энергии для получения нужного толчка производится самой системой, что гарантирует получение толчков в нужные моменты времени.

В 20 веке открыт новый тип резонанса, получивший название параметрического резонанса. Представим себе, что одна из физических величин («параметров»), определяющая свойства колебательной системы, сама периодически меняется. Таким параметром в случаях маятника или качелей может быть расстояние от оси колебаний до центра инерции системы.

При наличии малых колебаний системы периодическое изменение такого параметра может, при соответствующей частоте, привести к значительному усилению колебаний – это и есть параметрический резонанс.

Если качели совершают малые колебания, то эти колебания можно усилить, поднимаясь и приседая в «такт», т.е. меняя положение центра инерции системы относительно оси колебаний