1.2. Динамика поступательного и вращательного движения абсолютно твердого тела

Динамика – раздел механики, изучающий движение материальных тел в пространстве и времени совместно с причинами, вызывающими это движение.

1.2.1. Динамика поступательного движения абсолютно твердого тела

В основе динамики лежат законы И.Ньютона, сформулированные им в 1687 г. на основе экспериментальных данных и теоретических сведений, полученных Ньютоном и другими учеными.

I–й закон Ньютона. Если тело (материальная точка) не взаимодействует с другими телами или все взаимодействия скомпенсированы, то тело будет находиться в состоянии покоя или равномерного прямолинейного движения.

Такое тело называется свободным, а его движение – движением по инерции.

II–й закон Ньютона. Если взаимодействия с другими телами не скомпенсировано, то тело будет двигаться с ускорением, величина которого пропорциональна мере воздействия и обратно пропорционально мере инертности тела.

Инертностью называется способность тел противостоять изменению состояния движения.

III–й закон Ньютона. Тела оказывают друг на друга одинаковые по величине и противоположные по направлению воздействия.

При поступательном движении мерой механического воздействия на тела является сила . Это векторная величина. Сила представляет собой обобщенную замену реальных взаимодействий между телами.

Мерой инертности тела при поступательном движении является масса² m тела.

После введения понятий сила и масса, законы Ньютона можно сформулировать несколько иначе.

I-й закон Ньютона. Если на тело (материальную точку) не действуют ни какие силы или все действующие силы скомпенсированы, то тело будет находиться в состоянии покоя или равномерного, прямолинейного движения.

Законы Ньютона, как и остальные законы механики, выполняются не во всех системах отсчета. Системы отсчета, в которых выполняется I закон Ньютона, называются инерциальными системами отсчета.

Например, рассматривая движение тел внутри вагона, движущегося без ускорения, система отсчета, связанная с вагоном будет инерциальной системой. Однако при ускоренном движении вагона, система отсчета, связанная с вагоном будет неинерциальной системой. Обычно мы будем считать все системы отсчета, связанные с Землей или движущиеся относительно Земли равномерно и прямолинейно инерциальными. Строго говоря, все такие системы отсчета неинерциальны, однако, в большинстве случаев эффекты, обусловленные неинерциальностью земной системы отсчета, будут пренебрежительно малы.

II–й закон Ньютона. Если силы, действующие на тело, не скомпенсированы, то тело будет двигаться с ускорением , величина которого пропорциональна результирующей силе и обратно пропорционально массе тела m:

.

Второй закон Ньютона можно записать в другой форме с учетом, что

= ,

тогда = m =

или dt = .

Вектор называется импульсом. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру его движения (скорость), но и его важнейшую динамическую характеристику – массу.

Вектор dt называется элементарным импульсом силы .

III–й закон Ньютона. Тела взаимодействуют друг с другом силами равными по величине и противоположными по направлению.

.

= – .

= – .

Следовательно, при механическом взаимодействии двух тел изменения их импульсов численно равны и противоположны по знаку.

1.2.1. Динамика вращательного движения абсолютно твердого тела

Рассматривая вращательное движение, встает вопрос, можно ли применять законы Ньютона в виде, полученном для поступательного движения?

Д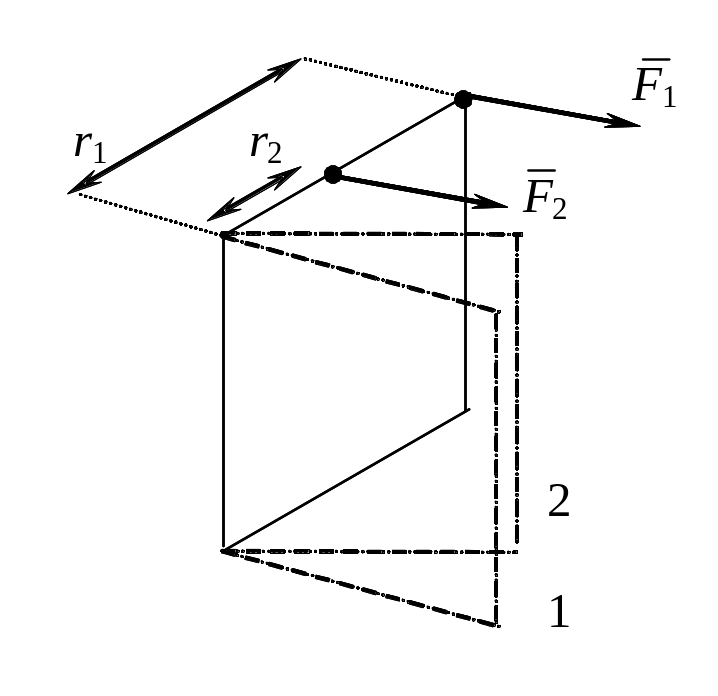 ля этого необходимо выяснить является ли сила – мерой воздействия, а масса – мерой инертности при вращательном движении твердого тела.

Если воздействовать на тело равными силами , но приложенными в разные точки (на расстоянии r₁ и r₂ от оси вращения, соответственно), то, если сила является мерой воздействия, результат воздействия должен быть одинаковым. Однако из эксперимента видно, что он разный. В первом случае угловое ускорение будет больше, чем во втором и, соответственно, угловой путь, пройденный телом за одинаковое время в первом случае больше, чем во втором (₁ >₂).

Следовательно, сила не является мерой воздействия при вращательном движении. В качестве меры воздействия вводится понятие момента силы.

М омент силы равен векторному произведению радиус-вектора , проведенному от оси вращения в точку приложения силы , на эту силу, т.е.

= [ ].

Величина момента силы

М = F r sin,

где  – угол между векторами и .

Н аправление вектора момента силы может быть определено по "правилу правого винта”: если при вращении правого винта вектор силы касателен к этому вращению, то поступательное движение винта совпадает по направлению с вектором момента силы .

Рассмотрим движение по наклонной плоскости двух цилиндров одинаковой массы (m₁ = m₂), одинаковых геометрических размеров (d₁ = d₂, l₁ = l₂), с одинаковым материалом поверхности (коэффициенты трения одинаковы, k₁ = k₂), т.е. силы, действующие на цилиндры одинаковы, но имеющих разное распределение масс по объему (первый – сплошной, второй – полый). Если масса является мерой инертности тела, то к основанию наклонной плоскости оба цилиндра должны скатиться одновременно. Однако из эксперимента видно, что первый цилиндр скатывается быстрее, чем второй.

Масса не является мерой инертности при вращательном движении а.т.т.

В качестве меры инертности вводится понятие момента инерции.

М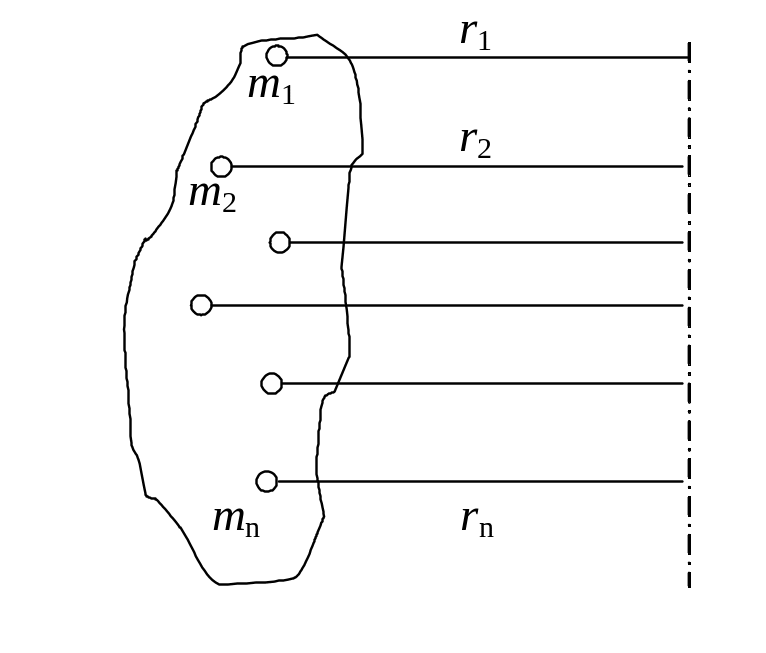 омент инерции тела относительно неподвижной оси равен сумме произведений всех материальных точек тела на квадраты их расстояний до оси.

I =

Таким образом, основываясь на законах Ньютона, можно записать законы динамики вращательного движения твердого тела.

Основной закон динамики вращательного движения твердого тела. Если моменты сил, действующие на тело, не скомпенсированы, то тело будет двигаться с угловым ускорением, величина которого пропорциональна результирующему моменту сил и обратно пропорционально моменту инерции.

Этот закон можно записать в другой форме с учетом, что

= ,

тогда = I =

или dt = = .

Вектор = называется моментом импульса. Эта величина, как и импульс тела при поступательном движении, является важной динамической характеристикой.

1.2.1.1. Моменты инерции некоторых тел

а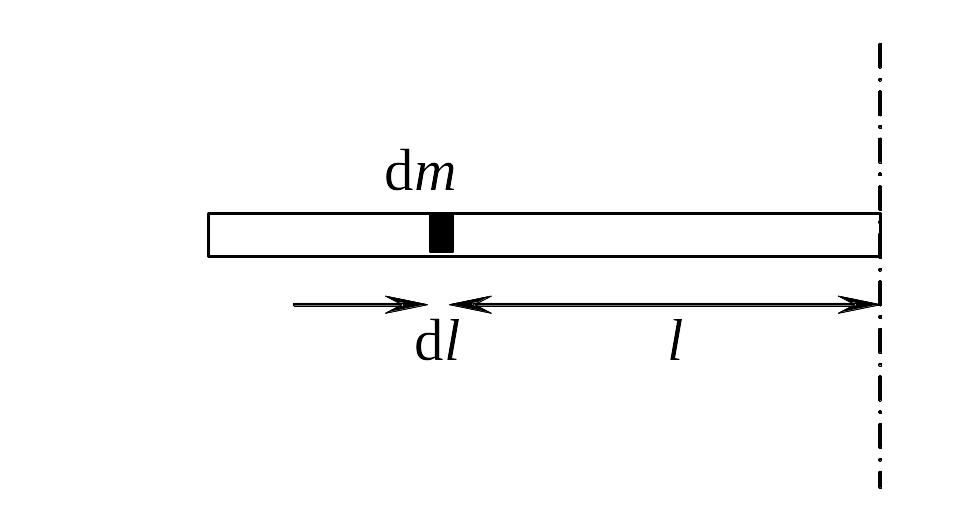 ) момент инерции стержня относительно оси, проходящей через конец стержня перпендикулярно к нему.

На стержне выделим элементарный отрезок размером dl на расстоянии l от оси вращения. Элементарная масса dm отрезка стержня размером dl может быть найдена как

dm =  dl,

где  = – линейная плотность стержня.

Момент инерции отрезка dl массой dm, находящегося на расстоянии l от оси вращения

dI = .

Тогда момент инерции всего стержня

I = .

Так как масса стержня m=L, то

I = mL²

б) момент инерции диска относительно оси, проходящей через центр диска перпендикулярно к нему.

На диске выделим кольцо толщиной dr на расстоянии r от оси вращения. Элементарная масса dm кольца толщиной dr может быть найдена как

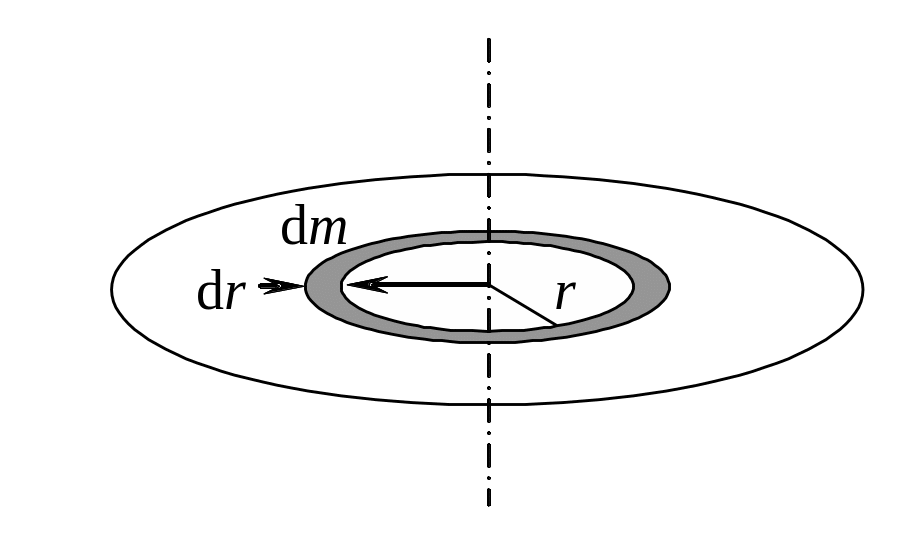
dm =  ds =  2r dr,

где = – поверхностная плотность диска.

Момент инерции кольца толщиной dr массой dm, находящегося на расстоянии r от оси вращения

dI = .

Тогда момент инерции всего диска

I = .

Так как масса диска m= R², то

I = m R².

в) момент инерции сплошного однородного шара относительно оси, проходящей через его центр.

В шаре вырежем диск толщиной dr на расстоянии r от оси вращения. Момент инерции диска радиусом а = и массой dm равен

dI = .

Масса диска dm =  dV =  a² dr =   (R² – r²) dr,

где  – объемная плотность шара.

Т огда момент инерции

=

= (R⁵ – R⁵ + R⁵) = R⁵.

Так как масса шара m = R³, то I = m R².

1.2.1.2. Теорема Штейнера

Для нахождения момента инерции тел относительно произвольных осей используется теорема Штейнера.

М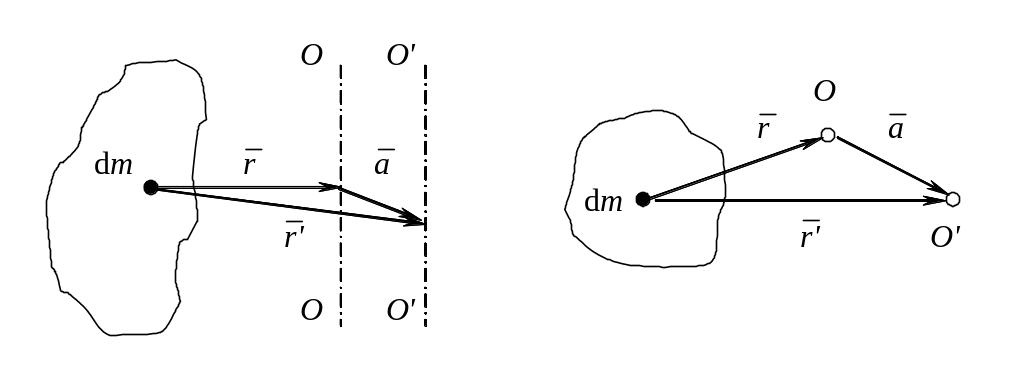 омент инерции I тела относительно произвольной оси равен сумме момента инерции I₀ тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a² между осями.

I = I₀ + m a²

Найдем момент инерции I_O' тела относительно оси О' при условии, что известны момент инерции I_O тела относительно оси О и взаимное расположение осей О и О' (т.е. известны I_O, )

Момент инерции I_O' тела относительно оси О'

I_O' = .

Радиус-вектор или ,

а его численное значение r' ² = a² +2 +r².

Тогда

I_O' = = I_O +ma² + .

Если ось О проходит через центр масс тела, то

I_O' = I_О + m a².