Решение обыкновенных дифференциальных уравнений n-го порядка

Рассмотрим задачу Коши для ДУ второго порядка

Решение будем искать на интервале . Сведем это уравнение к системе ДУ первого порядка, состоящей из двух уравнений.

Рассмотрим, как решить эту задачу с использованием функции rkfixed. Функцию определим как вектор с двумя элементами

Пример

Решение ищем на отрезке [1,4].

Сначала найдем аналитическое решение задачи Коши для этого примера:

.

Разрешим данное ДУ относительно второй производной 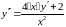. Запишем функцию : . Воспользуемся функцией пакета rkfixed.

Сплошная линия – интегральная кривая, а вторая кривая – график первой производной.

В таблице в первом столбце выведена переменная x, во втором столбце – искомая функция, а в третьем –­ первая производная искомой функции.

Полученное решение можно сравнить с аналитическим решением, найденным выше.

В отчет надо включить таблицу с результатами аналитического и численного решения и сравнить их.

Для ДУ более высокого порядка будем использовать тот же метод, что и для ДУ второго порядка. Тогда вектор начальных условий и функция будут содержать элементов.

Задание

1. Найти аналитическое решение задачи Коши.

2. Решить задачу Коши, используя функции rkfixed или Rkadapt или Bulstoer.

3. Построить интегральную кривую и график первой производной, вывести таблицы полученных результатов и сравнить их (вывести таблицу разностей).

Отчет оформить как файл пакета MathCad.

Варианты задания для этой работы взять в работе №3.

Опишем возможности пакета MathCad для решения жестких систем дифференциальных уравнений.

Жесткие системы дифференциальных уравнений

Система дифференциальных уравнений, записанная в матричной форме y=A*X , где А – почти вырожденная матрица, называется жесткой. В этом случае решение, возвращаемое функцией rkfixed может быть неустойчивым. Для решения жестких систем в пакете есть специальные функции: Stiffb, Stiffr, stiffb, stiffr. Функции Stiffb и stiffb используют метод Булирша-Штера соответственно с постоянным и переменным шагом. А функции Stiffr и stiffr используют метод Розенброка соответственно с постоянным и переменным шагом.

Метод Розенброка решения жестких систем дифференциальных уравнений (y и f – векторы, t – независимая переменная) заключается в следующем: 1. На каждом шаге вычисляется матрица производных в точке : ; 2. следующая точка находится из матричного уравнения:

,  в котором постоянные параметры алгоритма имеют, к примеру, такие значения: .

Таким образом, алгоритм Розенброка является одношаговым и явным (не требуется решения нелинейных уравнений на каждом шаге). Однако пересчет каждого шага требует   численного определения производных функции и решения системы линейных уравнений (т.к. искомые компоненты вектора входят в матричное уравнение в линейной комбинации).

Алгоритм Розенброкка, благодаря своей вычислительной простоте, реализован не только в пакете MathCad , но и во многих других математических пакетах.

Вид матрицы, возвращаемой этими функциями, совпадает с возвращаемым функцией rkfixed. Однако эти функции требуют задания дополнительных аргументов.

Функции Stiffb, Stiffr имеют следующие аргументы:

­­– вектор начальных условий размерности , где – порядок дифференциального уравнения или число уравнений в системе ОДУ ( если решается система уравнений);

– граничные точки интервала, на котором ищется решение ДУ. Начальные условия, заданные в векторе , – это значение решения в точке ;

– число точек (не считая начальной), в которых ищется приближенное решение. Этот аргумент определяет число строк в матрице, возвращаемой функциями Stiffb, Stiffr;

– функция, возвращающая значение в виде вектора из элементов, содержащих первые производные неизвестных функций;

– функция, которая возвращает матрицу размером . Первый столбец содержит производные . Остальные строки и столбцы представляют собой матрицу Якоби системы ОДУ. Например, если

, то .

Если надо найти приближенное решение задачи Коши только в конечной точке интервала, то для жестких систем используют функции stiffb, stiffr.

Рассмотрим только те параметры, которых нет в функциях Stiffb, Stiffr:

– параметр, контролирующий точность решения. Малое значение заставляет алгоритм брать меньшие шаги вдоль траектории, что увеличивает точность решения. Значения, близкие к 0.001, дают хорошую точность решения;

– максимальное число промежуточных точек, в которых ищется приближенное решение. Значение ограничивает сверху число строк матрицы, возвращаемой функцией;

– минимально допустимый интервал между точками, в которых ищется приближенное решение. Он определяет нижнюю границу различия между любыми двумя числами в первом столбце матрицы, возвращаемой функцией.

Работа № 3