Лекция 2. Векторы
В лекции обсуждаются основные понятия таких разделов как векторное исчисление и матричный анализ.
2.1. Геометрические векторы
Вектор
- направленный отрезок АВ
прямой, у которого различают начало -
точку А
и конец - точку В.
Обозначают так
.
К
понятию вектора, как величины,
характеризуемой и числом и направлением,
приводят многие задачи прикладных наук
и математики. Сила, скорость - векторные
величины,
они характеризуются и числом
и направлением;
площадь, объем, температура - величины
скалярные,
для их характеристики достаточно
числового
значения.
Длиной
или модулем
вектора называется
длина направленного отрезка. Обозначается
модуль вектора так
.
Вектор, начало и конец
которого
совпадают, называется нуль-вектором.
Модуль
нуль-вектора равен нулю, а направление
его неопределенное. Вектор, модуль
которого равен единице, называется
единичным.
Два
вектора считаются тождественными
или
равными, если один из них может быть
получен из другого с помощью параллельного
переноса. Рассмотрим векторы, которые
можно свободно перемещать в пространстве,
соблюдая условия параллельности, не
меняя направления и длины. Их называют
свободными
векторами.
2.2. Линейные операции над векторами
Над векторами можно производить линейные операции: умножение на число и сложение.
Векторы,
лежащие на одной и той же прямой или на
параллельных прямых называются
коллинеарными.
Произведением числа
на вектор
и называется вектор, коллинеарный
вектору
,
длина которого равна
и который одинаково направлен с вектором
,
если
> 0 и противоположно направлен,
если
< 0. В частности, умножение данного
вектора
на
-1 дает противоположный вектор -
,
а
умножение на 0 дает нуль-вектор. При этом
=
.
Условие
коллинеарности двух векторов
и
такое:
=
(2.1)
Сложение векторов.
С
ложение
двух векторов выполняется по правилу
параллелограмма. Суммой двух векторов
и
называется
третий вектор
,
имеющий
с ними общее начало и совпадающий с
диагональю параллелограмма, построенного
на векторах
и
как
на сторонах (рис. 2.1).
С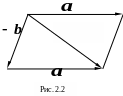
уммой
нескольких векторов
+
+
+…+
является вектор,
соединяющий
начало вектора
с
концом
вектора
(по правилу замыкающей стороны
многоугольника). О свойствах сложения
векторов будет сказано ниже.
Разность двух векторов определяется как сложение с противоположным вектором:
- = +(- )= (рис. 2.2).
В частности, - =0.
2.3. Проекция вектора на ось
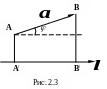
Имеется
в виду ортогональная проекция
пространственного вектора,
например,
на
направленную прямую
или другой вектор
.
При
этом проекциями начала и конца вектора
являются
основания перпендикуляров 
и
,
опущенных из точек А
и В
на ось
(рис. 2.3).
Проекцией вектора ось называется произведение модуля вектора на косинус угла между вектором и осью.
пр.
,
(2.2)
где
.
Модуль
величина
положительная или равная
нулю,
а сомножитель 
может быть положительным, отрицательным
или равным нулю. От этого зависит и знак
проекции:
,
если
,
если
,
если
