6.5. Асимптоты

Прямая называется асимптотой кривой , если расстояние от точки М кривой до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-нибудь ветви кривой.

Асимптоты могут быть вертикальные, наклонные, горизонтальные. Вертикальным асимптотами являются прямые ; где а – точка бесконечного разрыва функции.

Наклонные асимптоты, это прямые вида , где

; . (6.1)

Горизонтальные асимптоты Получаются как частный случай наклонных асимптот, когда .

Пример 6.7. Найти асимптоты графика функции .

Решение. Здесь , так как при функция не существует, а при функция неограниченно возрастает. Следовательно, прямая - вертикальная асимптота. Проверим теперь, существуют ли наклонные асимптоты вида этой функции. Для этого по формулам (6.1) вычислим :

.

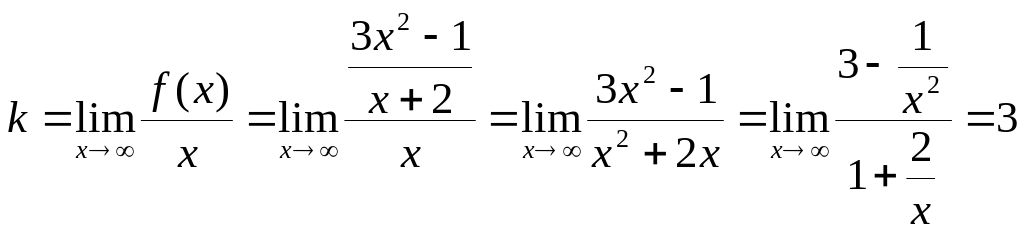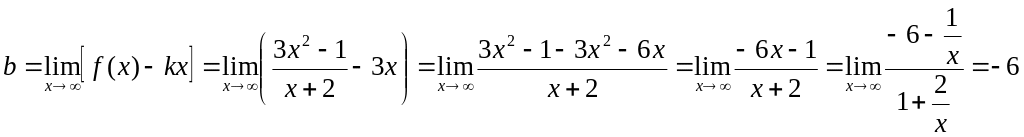
Итак, уравнение наклонной асимптоты .

Найденные асимптоты значительно облегчают правильное построение графика функции.

6.6. Схема общего исследования функции и построения ее графика

Предлагается примерная схема исследования функции:

1. Находят область определения, точки разрыва, интервалы непрерывности.

2. Исследуют функцию на четность или нечетность, что позволяет судить о наличии (отсутствии) осевой или центральной симметрии графика.

3. Находят точки пересечения графика с осями координат («нули» функции), если они существуют.

4. Находят асимптоты, если они существуют.

5. Находят точки экстремума и интервалы монотонности функции.

6. Находят точки перегиба и интервалы выпуклости и вогнутости кривой.

7. По результатам исследования строят график функции.

Пример 6.8. Исследовать функцию и построить ее график.

Решение. Будем придерживаться предложенной выше схемы исследования.

1. Функция определена при всех значениях , кроме тех, при которых знаменатель , то есть, кроме и . Таким образом, область определения функции . Точки и являются точками бесконечного разрыва:

, ;

, .

2. Исследуем функцию на четность. Для этого подставим в ее формулу вместо . Получим , то есть . Это показывает, что функция нечетная, а ее график симметричен относительно начала координат, что позволяет ограничиться исследованием функции для и перенести результаты влево симметрично точке .

3. Найдем «нули» функции. Полагая , видим, что , и обратно, если , то . Это значит, что график функции проходит через начало координат.

4. Из пункта 1 данного исследования видно, что прямые , являются вертикальными асимптотами. Найдем наклонные асимптоты, пользуясь формулами (6.1):

;

.

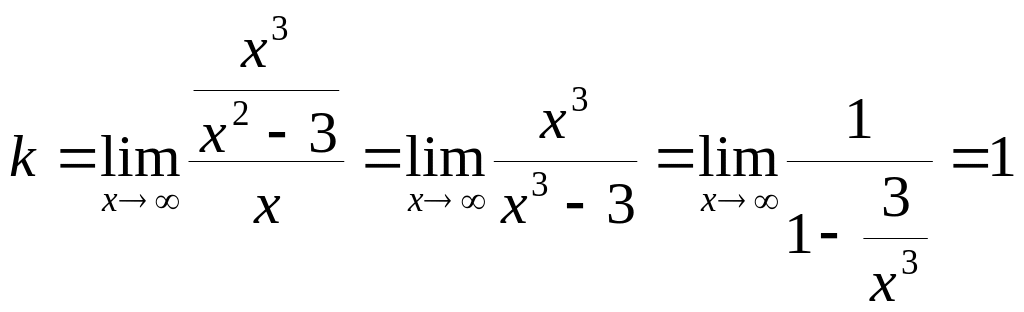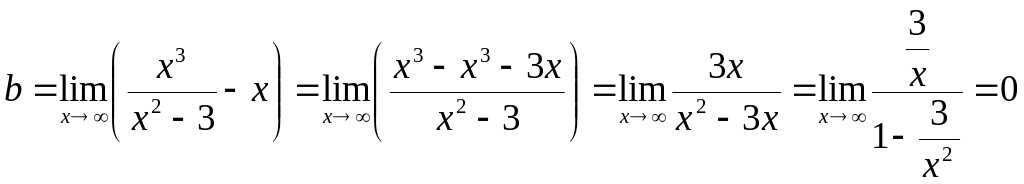Итак, уравнение наклонной асимптоты . Проведем асимптоты (рис.6.7), это облегчит построение графика функции.

5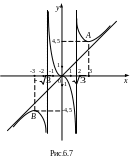 . Теперь исследуем функцию на экстремум по правилу, изложенному в §6.2.3. Ее первая производная будет равна нулю, если числитель дроби равен нулю, то есть или . Корни последнего уравнения , , являются критечкими точками первого рода. Производная не существует, если , но корни этого уравнения не входят в область определении функции и не могут быть критическими точками.

Сначала проверим характер экстремума в точке . В ее окрестности возьмем достаточно близкие две точки и . Легко видеть, что производная не меняет знак при переходе через точку , в самом деле , а значит, что функция монотонно убывает и точка не является точкой экстремума.

Перейдем к точке . Возьмем в ее окрестности две достаточно близкие точки и . Определим знаки производных в этих точках: , . Так как производная меняет знак с минуса на плюс, то - точка минимума. Найдем ее ординату, вычислив значение функции при . Получим . Итак, точка А(3; 4,5) есть точка минимума (рис.6.7). Ввиду симметрии графика относительно начала координат, точка В(-3; -4,5) является точкой макисмума.

Функция возрастает, если ; убывает, если .

6. Найдем точки перегиба и интервалы выпуклости и вогнутости графика функции. Для этого потребуется вторая производная функции . Вторую производную приравниваем к нулю. Она равна нулю, если числитель или , откуда - корень уравнения и точка возможного перегиба. Проверим меняет ли знак вторая производная при переходе через . Возьмем две точки и в окрестностях нуля. Оценим знак второй производной в этих точках , . Так как знак второй производной поменялся на противоположный при переходе через точку , то - точка перегиба, ее ордината - это начало координат.

Интервалы выпуклости графика , интервалы вогнутости .

Строим график. Он должен соответствовать результатам исследования.

Лысенко Валентин Иванович

Гофман Виктор Гершонович